해당 포스팅은 "이것이 취업을 위한 코딩 테스트다 with 파이썬" 책을 기반으로 포스팅 하였습니다. ✍️✍️
이진 탐색
순차 탐색
순차 탐색은 리스트 안에 있는 특정한 데이터를 찾기위해 앞에서부터 순서대로 데이터를 하나씩 확인하는 방법이다. 이 방식은 정렬이 되지 않은 리스트에서 원하는 특정 데이터를 시간만 있다면 찾아낼 수 있다는 장점이 있다.
순차 탐색의 파이썬 코드는 다음과 같다.
# 순차 탐색 소스코드 구현
def sequential_search(n, target, array):
# 각 원소를 하나씩 확인
for i in range(n):
# 현재 원소가 찾고자하는 원소와 동일 하면
if array[i] == target:
return i + 1 # 현재 위치 반환
print("생성할 원소 개수를 입력한 다음 한 칸 띄고 찾을 문자열을 입력하세요.")
input_data = input().split()
n = int(input_data[0]) # 원소 개수
target = input_data[1] # 찾고자 하는 문자열
print("앞서 적은 원소 개수만큼 문자열을 입력하세요. 구분은 띄어쓰기 한 칸으로 합니다.")
array = input().split()
# 순차 탐색 수행 결과 출력
print(sequential_search(n, target, array))이러한 순차 탐색은 데이터 개수가 N개 일 때 최대 N번의 비교 연산이 필요하므로 최악의 경우의 시간 복잡도가 O(N)이다.
이진 탐색
이진 탐색은 순차 탐색과 달리 이미 정렬이 되어 있어야만 사용할 수 있는 알고리즘이다.
이진 탐색은 위치를 나타내는 변수를 3개 사용하는데, 이는 탐색하고자 하는 범위의 시작점, 끝점, 그리고 중간점이다.
즉, 찾고자 하는 데이터와 중간점에 위치한 데이터를 비교하며 어느 쪽에 원하는 데이터가 있을지 찾아가는 방식이다.
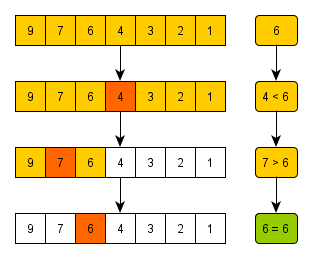
따라서 이진 탐색 알고리즘은 한 단계마다 평균적으로 원소가 절반씩 줄어든다.
따라서 이를 빅오 표기법으로 나타내면 O(logN)이라고 할 수 있다.
이러한 이진 탐색을 구현하는 방법 중 재귀함수를 이용한 코드는 다음과 같다.
# 이진 탐색 코드 (재귀 함수 사용)
def binary_search(array, target, start, end):
if start > end:
return None
mid = (start + end) // 2 # 중간점
# 찾은 경우 중간 인덱스 반환
if array[mid] == target:
return mid
# 중간점의 값보다 찾고자 하는 값이 작은 경우 왼쪽으로
elif array[mid] > target:
return binary_search(array, target, start, mid - 1)
# 중간점의 값보다 찾고자 하는 값이 큰 경우 오른쪽으로
else:
return binary_search(array, target, mid + 1, end)
# 원소의 개수 n과 target 입력받기
n, target = list(map(int, input().split()))
# 전체 원소 입력받기
array = list(map(int, input().split()))
# 이진 탐색 수행 결과 출력
res = binary_search(array, target, 0, n - 1)
if res == None:
print("원소가 존재하지 않습니다.")
else:
print(res + 1)단순하게 반복문을 사용하여 이진 탐색을 구현한 코드는 다음과 같다.
# 이진 탐색 소스코드 (반복문 사용)
def binary_search(array, target, start, end):
while start <= end:
mid = (start + end) //2
# 찾은 경우 중간 인덱스 반환
if array[mid] == target:
return mid
# 중간점의 값보다 찾고자 하는 값이 작은 경우 왼쪽으로
elif array[mid] > target:
end = mid -1
# 중간점의 값보다 찾고자 하는 값이 큰 경우 오른쪽으로
else:
start = mid + 1
return None
# 원소의 개수 n과 target 입력받기
n, target = list(map(int, input().split()))
# 전체 원소 입력받기
array = list(map(int, input().split()))
# 이진 탐색 수행 결과 출력
res = binary_search(array, target, 0, n - 1)
if res == None:
print("원소가 존재하지 않습니다.")
else:
print(res + 1) 위의 코드들을 보면 이진 탐색 소스코드 작성이 어렵지 않다고 수 있지만, 참고자료가 없는 상황에서 이를 정확히 구현하기는 생각보다 까다로울 수 있다.
이진탐색은 코딩 테스트에서 자주 나오는 문제이므로 위 코드를 여러번 작성하며 외워두자. 특히, 데이터의 범위가 큰 상황에서 탐색을 하는 상황이 온다면, 이진 탐색으로 접근해보자.
트리 자료구조
이진 탐색 알고리즘은 이미 정렬이 되어있는 데이터들에 대해 사용가능하였다. 프로그램에서는 데이터를 정렬해두는 경우가 많아 이진탐색을 효과적으로 사용할 수 있는데, 실제 데이터베이스에서는 이를 트리 자료구조를 이용하여 정렬한다. 따라서 데이터베이스에서는 이진 탐색과는 다른 유사한 방식으로 항상 빠른 탐색이 가능하게 설계되어 있다.
이때 사용하는 트리 자료구조는 다음과 같다.
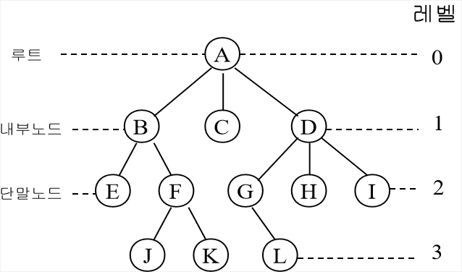
트리 구조는 일부를 떼어내어도 여전히 트리구조의 형태를 유지하고 있다.
이러한 트리를 서브 트리라고 부른다.
이 트리 자료구조는 파일 시스템과 같이 계층적이고 정렬을 해야하는 데이터에 사용하기 적합하다.
그러면 이러한 트리 구조를 이용하여 어떤식으로 이진탐색이 진행되는지 알아보자.
이진 탐색 트리
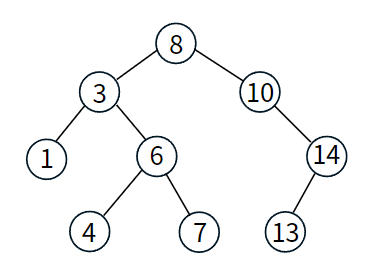
이진 탐색 트리의 특징
- 부모 노드의 왼쪽 부분 자식노드들은 더 작은 값을 가지고 있다.
- 부모 노드의 오른쪽 부분 자식노드들은 더 큰 값을 가지고 있다.
즉, 이진 탐색 트리는 왼쪽 자식 노드 < 부모 노드 < 오른쪽 자식 노드 순으로 데이터가 정렬되어 있는 형태이다.
이러한 이진 탐색 트리는 알고리즘보다는 자료구조 쪽이며, 코딩 테스트에서 이를 구현하도록 요구하는 경우는 거의 없으므로 구현 코드는 생략하자. 따라서 이진 탐색 트리가 구현되어 있는 상황에서 데이터를 탐색하는 방식만 간단히 살펴보자.

이미지 출처: https://medium.com/swlh
위 참고자료는 찾는 원소가 27일 때 동작하는 과정이다.
이진 탐색 트리를 이용한 탐색과정을 정리하면 다음과 같다.
부모 노드와 찾고자 하는 원소값 간의 크기 비교를 한 후, 왼쪽 자식노드로 이동할지, 오른쪽 자식노드로 이동할지 결정한다. 이 과정을 찾고자 하는 값과 동일한 노드에 도달할 때까지 반복한다.
이 동작원리는 매우 직관적이며 간단하다.
++ 참고
이진 탐색 문제의 경우에는 보통 데이터 범위가 매우 많은 경우에 사용된다. 이런 경우에 데이터를 input() 함수로 받게되면, 동작 속도가 느려 시간 초과로 오답이 될 수 있다. 이처럼 입력 데이터가 많은 경우에는 sys 라이브러리의 readline() 함수를 이용하여 보다 효율적인 입력 방식을 사용하도록 하자.
import sys
# 하나의 문자열 데이터 입력받기
input_data = sys.stdin.readline().rstrip()
#입력받은 문자열 그대로 출력
print(input_data)readline() 까지만 작성을 하면, 데이터 입력 후 엔터 줄바꿈 기호가 입력이 되어, 이 부분을 제거하기 위해 rstrip() 함수를 함께 사용해 주어야 한다. 위 코드는 외워두도록 하자.

