[백준 알고리즘 #11660] 구간 합 구하기5

시작하며

1차원 누적합 개념만으로 2차원 누적 합 문제를 풀고자할 때, 시간복잡도 문제에 걸릴 수 있다. (참고 : [백준 알고리즘 #11660] 구간 합 구하기4) 2차원의 경우는 단순 배열의 직전 요소와 현재 요소까지 누적하면 된다. 하지만 2차원 누적 합의 경우는 좀 다르다. 2차원의 경우는 현재 요소의 행과 열을 포함, 그 상위 내에 포함하고 있는 모든 요소를 더해 '누적 합 2차원 배열'을 만든다는 점이 다르다.

[1차원 누적 합]

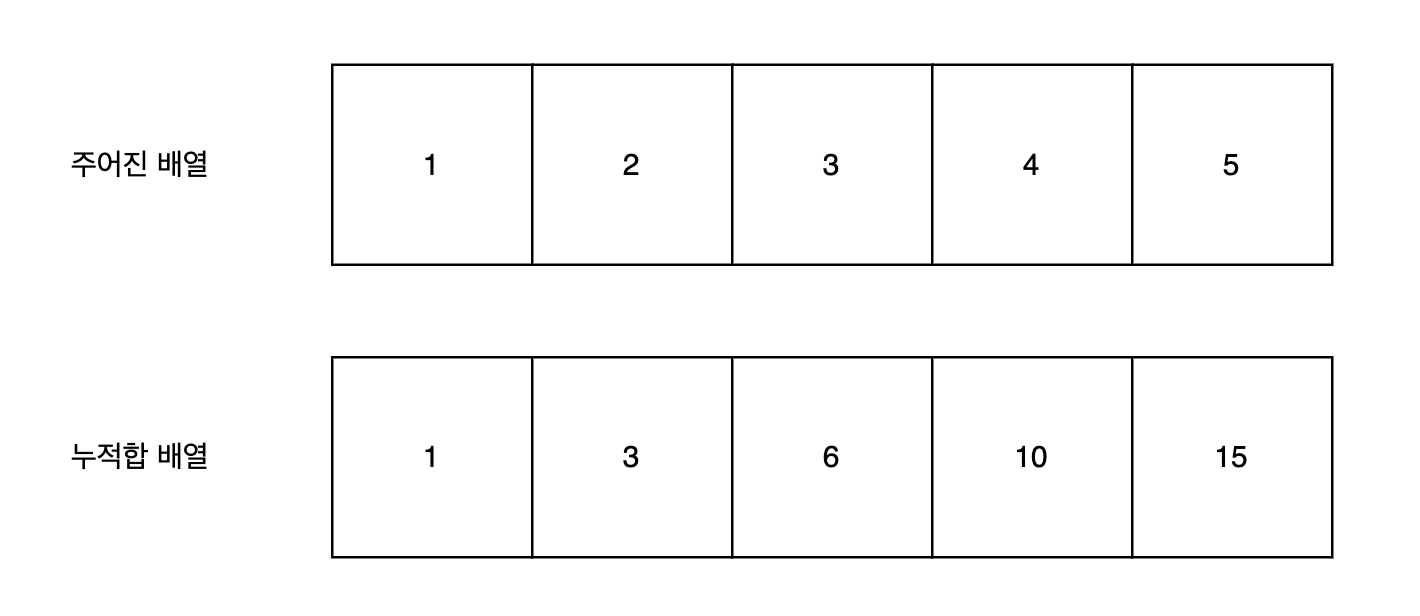
문제를 풀면 초기 배열을 제시해준다. 이때 알고리즘 해결 개발자는 '누적합 배열'을 위처럼 미리 만들어 둔다. 그 후, 구간 누적 합을 구하고자 할 때, 단순 인덱싱 조회를 통해 반복을 추가로 사용하지 않고 누적합을 구할 수 있다.

좀 더 풀어서 설명해 보자면, 구간 합을 구하는 횟수가 여러번 있다 했을 때, 1에서 3까지 또는 2에서 4까지 또는 3에서 5까지 구해야 한다 해보자. 이때 진행돼는 총 반복 횟수는 9번이다.

하지만 누적합 배열을 미리 정해둔다면? 초기 누적 합 배열을 구하기 위해 5번의 반복문 사용하면 되는 것이다. 1에서 3까지 구해야 한다면 '누적합 배열'의 2번 인덱싱을, 2에서 4까지 구해야 한다면 4번 인덱싱 후 0번 인덱스를 빼주면 되고, 3에서 5번까지 구해야 한다면 5번 인덱싱 후 2번을 인덱싱하여 그 값을 빼주면 되는 것이다.

[2차원 누적 합]

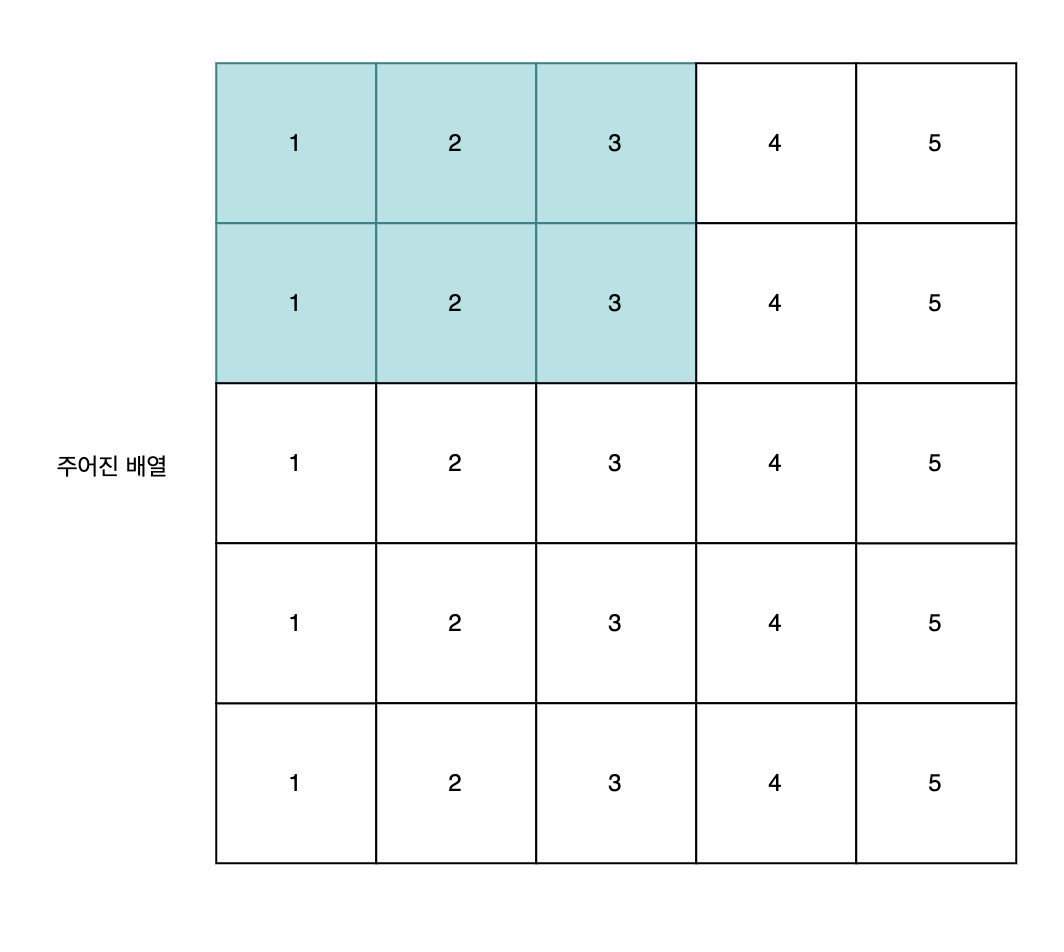
문제에서 2차원 배열을 제시해준다. 그리고 누적 합 배열을 생성한다 해보자. 그 때, 2행 3열의 누적합을 구하기 위해선 위 사진처럼 색칠 부분을 모두 더해준다. 그렇다면 만들어지는 누적 합 배열은 아래와 같다.

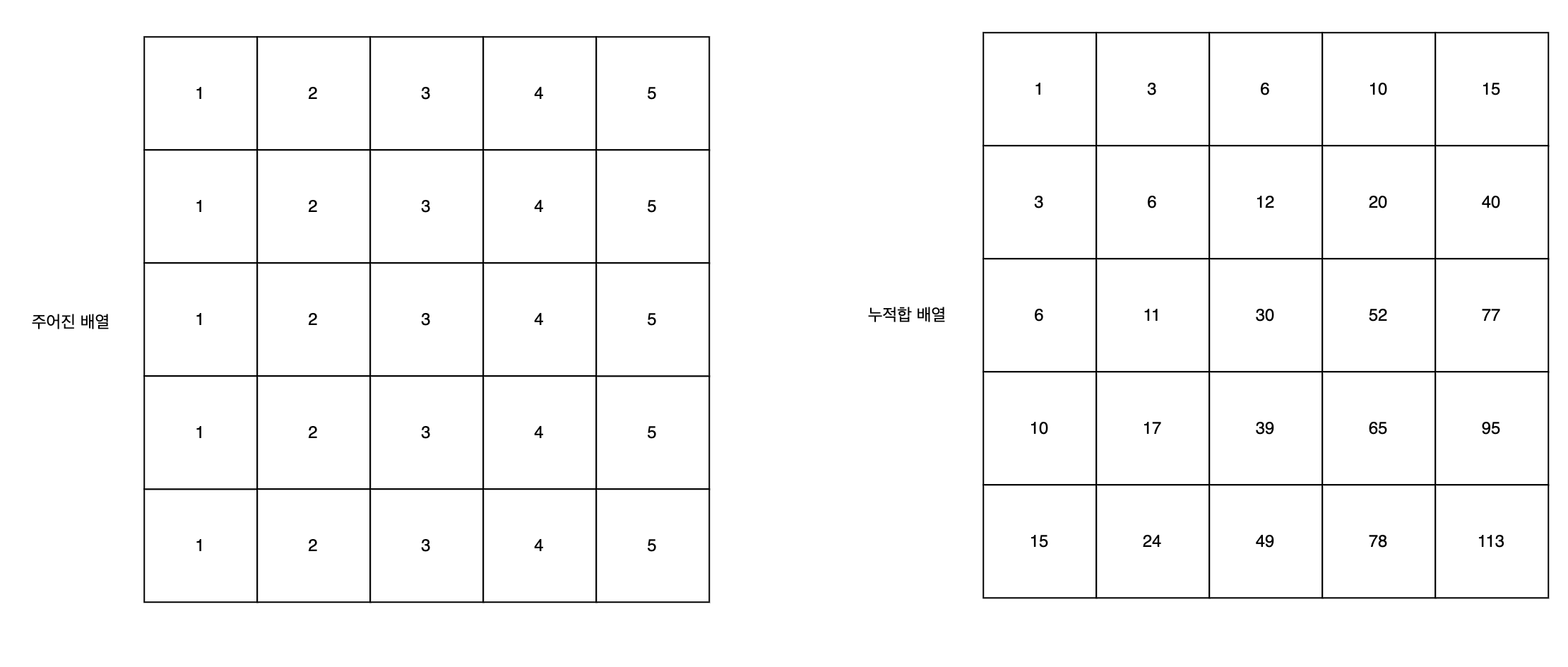
이 또한 1차원 누적 합처럼,초기 25번의 반복문 실행만으로 추후 누적합을 구하고자할 때, 단순 인덱싱만으로 누적 합을 구할 수 있는 것이다.

11660문제

fun main() {
    val (tableSize, sumCount) = readln().split(' ').run { get(0).toInt() to get(1).toInt() }
    val accumeratedTable = Array(tableSize + 1) { Array(tableSize + 1) { 0 } }
    val sb = StringBuilder()

    for (outterIndex in 1 .. tableSize) {
        val tableRow = readln().split(' ').map { it.toInt() }
        for (innerIndex in 1 .. tableSize) {
            accumeratedTable[outterIndex][innerIndex] = tableRow[innerIndex - 1] + (accumeratedTable[outterIndex][innerIndex - 1] + accumeratedTable[outterIndex - 1][innerIndex]) - accumeratedTable[outterIndex - 1][innerIndex - 1]
        }
    }

    for (index in 0 until sumCount) {
        val (x1, y1, x2, y2) = readln()
            .split(' ')
            .map { it.toInt() }

        sb.append("${accumeratedTable[x2][y2] - accumeratedTable[x2][y1 - 1] - accumeratedTable[x1 - 1][y2] + accumeratedTable[x1 - 1][y1 - 1]}\n")
    }
    println(sb)
}

최 상위 존재하는 반복문을 통해 '2차원 누적 합 배열'을 미리 구한다. 그 후, 구간 누적 합을 구하고자할 때, 인덱싱 작업만을 통해 입력에 필요한 최소 반복문 실행만으로(누적합 추출시엔 반복문 사용을 안함으로써) 정답을 도출한다.