An Efficient Utilization Test for Scheduling Hard Real-Time Sporadic DAG Task Systems on Multiprocessors

사담

RTSS에서 Sporadic/Periodic DAG Task Scheduling에 대한 논문을 찾던 중 RTSS 2019에 그럴듯한 제목의 논문을 발견하여 읽게 되었다. 지금까지 읽었던 논문들은 Task가 한 번 실행되고 끝나지만 이번 논문은 주기적으로 실행되는 Job 단위에서의 Scheduling에 대한 논문이다. 대신 이번 논문은 Scheduling Algorithm이 주가 아니라 새로운 Schedulability Test에 대해 소개하는 논문이다. 그래서인지 상당히 증명과 수식이 많은데, 이게 일반적으로 이론을 바탕으로 하는 논문에서 작성하는 패턴이라고 한다. critical path를 오히려 늦게 실행한다는 방식인 CP-GEDF은 새롭기는 했으나 직관적으로는 critical path를 먼저 실행하는게 좋을 것처럼 느껴져서 약간 의구심이 들었다. schedulability test 결과로는 더 많은 task set에 대해 schedulable하다는 것을 보였으나 critical path를 먼저 실행하는 알고리즘에 대해 적절한 schedulability test가 없어서 그렇지 더 좋은 scheduling algorithm는 있지 않을까 싶다.

Intro

Real-time system에서 중요한 개념 중 하나가 Schedulablility이다. 주어진 task set을 특정 알고리즘에 따라 스케줄링했을 때 모든 task의 모든 job이 deadline을 만족하면 (deadline 이전에 실행을 마친 경우) schedulable하다고 말한다. 당연히 한 task set이 schedulable한지는 실제로 스케줄링을 해보면 알 수 있지만, task set이 크면 시간이 많이 소요되기도 하고 경우의 수가 너무 많다. 따라서 utilization 등으로 스케줄링하지 않고 schedulability를 알 수 있는 방법에 대한 연구가 Real-time System 분야에서는 일반적으로 많이 진행된다. 이 논문은 Sporadic DAG task set에 대해 Lazy-Cpath Policy와 GEDF를 이용하여 스케줄링하는 상황에서 더 나은 schedulability test를 제공했다고 주장한다.

Contribution

GEDF를 사용하는 Multiprocessor에서 HRT(Hard-Real Time) Sporadic DAG task system에 대해 개선된 utilization-based schedulability test를 제시

System Model

System Model은 일반적으로 Real-time system에서 많이 사용하는 model이다.
n개의 sporadic DAG task를 가지는 $\tau = \{\tau_1, \dots, \tau_n\}$를 M개의 identical processor에 스케줄링하는 문제다. 각 task $\tau_i$는 $(G_i, d_i, p_i)$로 구성되며 각 task는 주기적으로 실행되는데 이 때 실행되는 단위를 job이라고 한다.

• $G_i$ : subtask $V_i$와 edge $E_i$로 구성된 $(V_i, E_i)$의 DAG. $\tau_i$의 k번째 subtask는 $\tau_i^{k}$로 나타낸다. ($\tau_i^{k}$의 j번째 job은 $\tau_{i,j}^{k}$으로 표기한다.) DAG의 특성 상 predecessor subtask가 모두 완료된 후에 실행 가능하다.
• $d_i$ : $\tau_i$의 deadline
• $p_i$ : $\tau_i$의 period. sporadic task이므로 연속된 job은 적어도 $p_i$만큼의 시간 간격을 가진다. 논문에서는 implicit deadline($d_i = p_i$)인 경우만 다룬다.

추가적인 용어들은 아래와 같다. 일반적으로 DAG task system에서 많이 쓰이는 용어들이다.

• chain : edge로 연결된 subtask들의 집합. chain 내 subtask들의 실행 시간의 합을 chain의 길이라고 한다.
• critical path : 가장 길이가 긴 chain. 길이가 같은 경우 임의로 하나를 고른다고 한다.
• $len(Cpath_i)$ : $\tau_i$의 critical path의 길이.
• cp-utilization $\sigma_i = len(Cpath_i)/p_i$
• $C_i$ : $\tau_i$의 모든 subtask의 실행 시간의 합
• utilization $u_i = C_i/p_i$
• total utilization $U_{sum} = \sum_{i=1}^{n}u_i$
• $\sigma_{max}(\tau) = max_{\tau_i \in \tau}\sigma_i$ (cp-utilization의 최대값)

또한 기본적으로 task set이 아래 조건을 만족한다.
1. $len(Cpath_i) \le p_i$ : critical path의 길이가 주기보다 길면 자명하게 스케줄 불가능하다.
2. $U_{sum} \le M$ : 스케줄 가능한 time slot의 총 합이 M이 utilization의 합이 M보다 큰 경우에도 자명하게 스케줄 불가능하다.

Lazy-Cpath Policy

이 논문이 기본적으로 사용하는 스케줄링 정책이다. 내용은 간단한데, 같은 DAG 내의 subtask 중 critical path에 있는 subtask의 우선도를 제일 낮게 준다는 것이다.
현재 실행 가능한 job들의 목록을 ready job이라고 하는데, 위 정책에 의하면 특정 시점에 critical path의 subtask들 중 1개만 ready job이 될 수 있다. (critical path 역시 하나의 chain이기 때문에 병렬적으로 실행할 수 없기 때문)
Real-time system에서 가장 많이 사용하는 스케줄링 정책인 GEDF (Global Earliest Deadline First)에 Lazy-Cpath Policy를 적용한 것을 앞으로 CP-GEDF로 표기하겠다. 따라서 CP-GEDF의 동작은 간단하게 아래와 같다.

1. 기본적으로는 deadline이 가장 짧은 job을 먼저 스케줄링 (preemption 가능하다.)
2. 그런 job이 M개보다 많은 경우에는 critical path가 아닌 job부터 스케줄링한다. non-critical path의 job들 사이에는 특별히 순서가 없다고 생각해도 무방하다.

[Lemma 1]

critical path의 subtask는 이전 subtask (predecessor)가 완료된 이후에 실행 가능하다.

pf)
귀류법으로 증명한다. $\tau_{i,j}^{x_{u+1}}$에 대해 $\tau_{i,j}^{x_u}$ 보다 나중에 끝나는 $\tau_{i,j}^{y_{1}}$ 이 있다고 가정하자. 그리고 $\tau_{i,j}^{y_{2}}$를 $\tau_{i,j}^{y_{1}}$ 의 predecessor job이라고 하자. (앞에 job이 끝나면 ready된다.) 이를 $\tau_{i,j}$의 release time인 $r_{i,j}$에 바로 ready되는 $\tau_{i,j}^{y_{w}}$ 이 있을 때까지 반복한다. ($\tau_{i,j}^{y_{1}}$이 있기 때문에 존재성은 입증되었다.) 이제 $\tau_{i}^{y_{w}}, \dots, \tau_{i}^{y_{1}}, \tau_{i}^{x_{u+1}}, \dots, \tau_{i}^{x_{k}}$이 critical path보다 길다는 것을 보이자.

각 time interval $[f_{i,j}^{y_{q+1}}, f_{i,j}^{y_{q}})$ (2≤ q ≤ w-1)은 두 가지 경우의 subinterval을 가진다.

1) $\tau_{i,j}^{y_{q}}$ 가 연속적으로 실행되는 구간
2) 실행되고 있지 않은 구간

1의 경우 critical path의 subtask 역시 실행 가능하다. 하지만 2의 경우에는 다른 subtask가 preemption하고 있어서 실행하지 못한다는 의미이므로 critical path의 subtask 역시 실행할 수 없다. (y가 붙은 subtask들은 critical path가 아니므로 lazy cpath에 의해 무조건 우선도가 높다.)
따라서 각 subinterval에 대해 y가 붙은 subtask들이 실행 시간이 더 길게 되고 명시한 chain이 critical path 보다 길어진다. 모순

[Lemma 2]

CP-GEDF로 스케줄링할 때 $\tau_{i,j}$는 마지막 subtask $\tau_{i}^{x_k}$의 job이 끝났을 때에 실행을 마친다.

pf)
Lemma 1과 같이 귀류법으로 증명 가능하다.

Schedulability Analysis

이 논문은 window-based reasoning framework를 기본으로 한다. window-based approach는 전체 task가 실행되는 스케줄을 여러 구간으로 나누고 이에 대해 각각 schedulability를 검사하겠다는 의미로 해석했다. 이를 위해 추가적으로 정의하는 용어들이 있다.

$[t_1, t_2)$ 가 아래 세 조건을 만족하는 경우 $\tau_i$의 executing critical path interval라 한다.

1. $\tau_{i,j}$가 $t_1$ 전에 release된다.
2. $t_2$보다 빨리 complete되지 않는다.
3. critical path의 subtask가 연속적으로 실행된다.

1, 2만 만족하는 경우는 non-executing critical path interval이라고 한다.

• busy interval : M개의 프로세서가 모두 실행중인 interval을 의미한다.
  
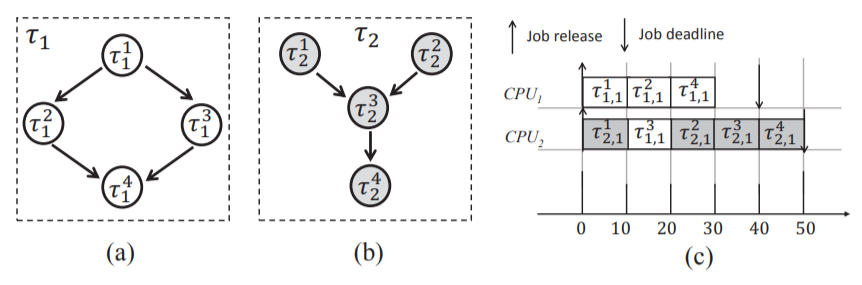
  예를 들어 그림에서 $\tau_2$의 executing critical path interval은 [10, 30), [30, 50)이며, [0, 30)은 busy interval이다.

[Lemma 3]

특정 interval $[t_1, t_2)$가 non-executing critical path interval이면 busy interval이다.

pf)
귀류법으로 non-executing인데 busy가 아니라고 가정하자. busy interval이 아니므로 적어도 한 processor가 idle하다.
또한 Lemma 2에 의해 아직 critical path 중 끝나지 않은 task가 존재한다. (critical path의 마지막 job이 끝났을 때 전체가 끝나므로) 따라서 Lemma 1에 의해, 그 중 ready인 job이 존재한다. 따라서 이 ready job이 실행되어야 하고 executing critical path interval이 되고 모순이다.

deadline miss의 필요조건

앞으로는 deadline miss가 일어나는 상황에 대한 필요조건에 대해 분석한다. 즉 deadline miss가 있는 경우 후에 언급할 condition들을 만족한다. 이를 위해 아래의 용어들을 더 사용한다. (용어가 정말 많다,,)

• $t_d$ : 처음 deadline miss가 일어나는 시간
• $\tau_h$ : problem task
• $\tau_{h, l}$ : deadline miss가 일어난 job (problem job)
• $[r_{h,l}, d_{h,l})$ : problem window
• workload : computation 시간의 합
• average workload : $[t, t+\Delta)$에서 average workload는 $\frac{W}{\Delta}$ 다.

[Lemma 4]

$\tau_{h, l}$ 이 deadline miss가 발생하면, $[r_{h,l}, t_d)$에서 non-executing critical path interval의 합은 $p_h - len(Cpath_h)$ 보다 크다.

pf)
Lemma 2에 의해 dag-job은 critical path의 마지막 subtask가 완료되면 완료된다. 그런데 $\tau_{h, l}$는 $t_d$까지 complete되지 않는다. critical path는 sequential하게 실행되야 하므로 period에서 critical path의 길이를 빼면 non-executing critical path보다 작아진다.

[Lemma 5]

$\tau_{h, l}$이 deadline miss인 경우 아래 식을 만족한다.
$\frac{W}{p_h} > M * ( 1 - \sigma_h) + \sigma_h$
($\sigma_h = \frac{len(Cpath_h)}{p_h}$, W : $[r_{h,l}, t_d)$에서의 workload)

pf)
$p_h$ 내의 executing critical path interval의 길이의 합을 $\alpha$라고 하면, non-executing critical path interval은 $p_h - \alpha$이다. lemma 3에 의해 non-executing은 busy interval이므로 $p_h - \alpha$만큼의 interval 동안은 M개의 프로세서를 모두 사용할 것이고, $\alpha$ 동안은 1개 이상의 프로세서를 사용한다. 따라서,

$W ≥ M * (p_h - \alpha) + \alpha > M * p_h - (M - 1) * len(Cpath_h)$

이다. (뒤의 등호는 deadline miss가 일어난 경우이므로 $\alpha < len(Cpath_h)$ 다.)

Window-based Analysis

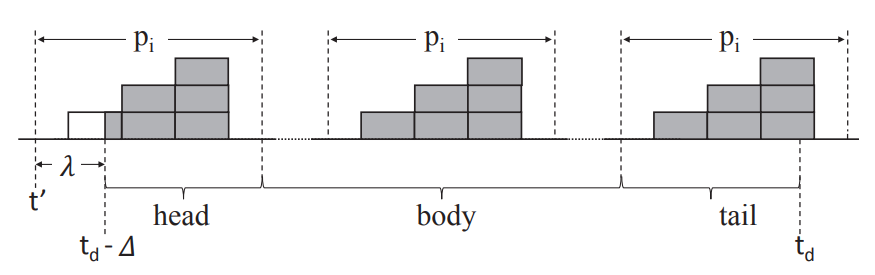
deadline이 일어난 임의의 DAG를 head, body, tail의 세 종류의 window로 나눈다. 간단하게 생각하기로는 interval의 시작에 있는 dag-job에 해당하는 interval이고, tail은 deadline에서의 dag-job에 해당하는 interval이며 body는 그 사이의 interval이다. 이렇게 나누는 이유는 body에 대해서는 하나의 dag-job에 대한 deadline miss에서의 필요조건을 구하면 이를 body에 있는 dag-job의 개수만큼 곱하여 적용 가능하기 때문이다. 또한 tail에 있는 dag-job은 스케줄 정책 상 무시된다고 하여 (이 이유는 잘 모르겠다.) body와 head에 대한 필요조건만 구하면 된다.

• carry-in job : head에 해당하는 interval 안에 있는 dag-job

• carry-in workload $\epsilon_i$ : carry-in job의 시간 t에서 남은 workload

• $\sigma_h-busy$ : average workload가 적어도 $M * ( 1 - \sigma_h) + \sigma_h$ 만큼 되는 interval

• maximal $\sigma_h-busy$ window : $t_d$로부터 뒤로 쭉 가면서 $\sigma_h-busy$인 최대 지점을 찾는다. 해당 지점이 $t_d-\Delta$일 때, $[t_d-\Delta, t_d)$ 를 maximal $\sigma_h-busy$ window 라고 한다.

[Lemma 6]

$\tau_h$는 각 $\sigma_h$에 대해 unique한 maximal $\sigma_h-busy$ window를 갖는다.

pf)
Lemma 5에 의해 $[r_{h,l}, t_d)$는 항상 $\sigma_h-busy$다. 따라서 존재성은 증명된다. maximal $\sigma_h-busy$ window의 정의에 의해 최대 지점을 찾으므로 유일성도 입증된다.

[Lemma 7]

$[t', t_d-\Delta)$ 에서의 average workload의 하한은 $(M-1)*\frac{\lambda-C_i+\epsilon_i}{\lambda}+1$이다.

pf)
$t' = t - \lambda$ ($\lambda$ : window의 시작으로부터 release time까지의 offset)라고 했을 때 head에서 실제 dag-job이 실행되기 전에 얼마나 skip되었는지의 상한을 구한다.

해당 interval에 세 종류의 workload가 존재한다.

1. dag-job $\tau_i$의 workload
2. $\tau_i$를 preempt한 다른 job의 workload
3. dag-job $\tau_i$와 병렬적으로 수행되는 workload

1의 경우 $\epsilon_i$ 가 $t_d-\Delta$에서 남은 dag-job 양이므로 workload는 $C_i - \epsilon_i$이다. 따라서 $\omega$를 M개의 프로세서가 모두 busy한 길이라고 하면 1+2의 workload 양은 $M*\omega+C_i-\epsilon_i$이다.

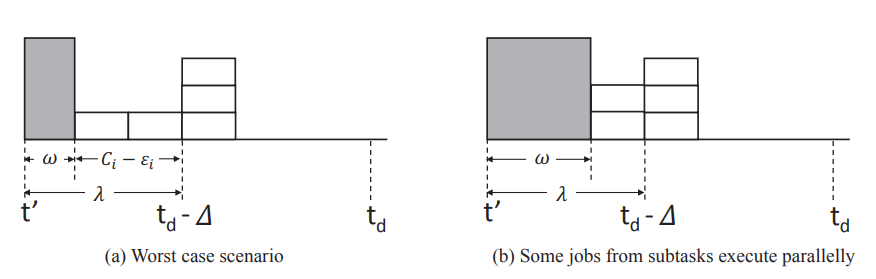
$\lambda$는 고정되어 있고 window 안에서 dag가 실행되는 양은 가변적이므로 $\omega$의 크기는 달라질 수 있다. dag-job이 다 sequential하게 실행되면 $\omega$는 그림의 왼쪽처럼 $\omega = \lambda - (C_i - \epsilon_i)$으로 제일 작다. 따라서 3번째 workload 종류를 무시한다고 생각하면 workload의 하한은 (하한을 구하는 것이므로 무시 가능하다.) 1+2의 workload 양을 $\lambda$로 나눈 것이다. 따라서 제일 작은 $\omega$ 값 대입하면 하한은 $(M-1)*\frac{\lambda-C_i+\epsilon_i}{\lambda}+1$으로 계산된다.

[Lemma 8]

maximal $\sigma_h-busy$ window $[t_d-\Delta, t_d)$에서의 carry-in workload의 상한은 $C_i-\sigma_h*\lambda$다.

pf)
$[t_d-\Delta, t_d)$ 가 maximal $\sigma_h-busy$ window이므로 $[t', t_d-\Delta)$ 에서의 average workload는 $M * ( 1 - \sigma_h) + \sigma_h$ 보다 작다. 따라서 Lemma 7에 의해

$(M-1)*\frac{\lambda-C_i+\epsilon_i}{\lambda}+1 < M*(1-\sigma_h)+\sigma_h$
(왼쪽은 average workload의 하한이다.)
따라서 식을 풀면 $0 ≤ \epsilon_h < C_i - (M-1)\sigma_h * \lambda ≤ C_i - \sigma_h*\lambda$

[Lemma 9]

$\tau_i$의 $[t_d-\Delta, t_d)$ 에서의 workload의 상한은 아래와 같다.

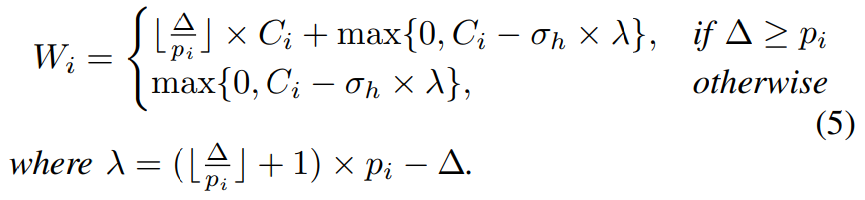
floor 기호가 있는 부분이 body에 대한 항이며, 뒤의 항이 head에 대한 항으로 생각하면 될 것 같다.

[Lemma 10]

$\tau_i$에 의한 maximal $\sigma_h-busy$ window $[t_d-\Delta, t_d)$에서의 average workload $W_i/\Delta$의 상한은 아래와 같다.

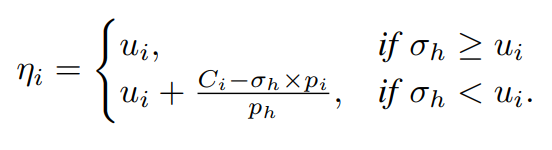
Lemma 9에서의 식을 $\Delta$로 나누고 잘 정리하면 나오는 듯 하다.

Utilization-based schedulability Test

[Theorem 1]

M개의 프로세서에서 CP-GEDF로 실행되는 n개의 독립적인 sporadic task에 대해 모든 task가 아래 조건을 만족하는 경우 스케줄 가능하다.

$\sum_{i=1}^{n}\eta_i \le M - (M - 1) * \sigma_k$
($\sigma_k = len(Cpath_h)/p_h$)

pf)

대우로 증명. CP-GEDF로 돌렸는데 deadline miss가 일어난다고 가정하자. $t_d$가 deadline이 일어나는 시점이고 $[t_d-\Delta, t_d)$ 가 maximal $\sigma_h-busy$ window라고 하자. maximal $\sigma_h-busy$ window는 lemma 5, 6에 의해 존재성은 증명되었다.

$\sigma_h-busy$ 이므로 $\frac{W}{\Delta} > M * ( 1 - \sigma_h) + \sigma_h$ 다. 그런데 lemma 10에 의해 $\frac{W_i}{\Delta} ≤ \eta_i$ 다. 따라서

$\sum_{i=1}^{n}\eta_i ≥ \sum_{i=1}^{n} \frac{W_i}{\Delta} ≥ \frac{W}{\Delta} > M * ( 1 - \sigma_h) + \sigma_h$ 이다.

대우 명제에 대해 증명이 되었으므로 원래 명제에 대해서도 참이다.

Ref

• Z. Dong and C. Liu, "An Efficient Utilization-Based Test for Scheduling Hard Real-Time Sporadic DAG Task Systems on Multiprocessors," 2019 IEEE Real-Time Systems Symposium (RTSS), Hong Kong, China, 2019, pp. 181-193, doi: 10.1109/RTSS46320.2019.00026.