본 사이트를 참고하여 정리한 내용입니다.
How to design the most powerful GNN
GNN의 가장 대표적인 활용 사례: graph 분류 작업
ex) 각 원자에 해당하는 graph와 feature를 기반으로, 전체 분자의 behavior 예측
그러나, GNN은 오직 node embeddings만을 학습한다.
❔ 어떻게 하면 node embeddings를 결합하여 노드단위가 아닌 '전체 graph embedding'을 만들어낼 수 있을까?
이 포스트의 주요 내용을 미리 정리하자면 다음과 같다.
1. global pooling 이라는 새로운 종류의 layer.
(node embeddings를 결합하기 위함)
2. GIN 이라는 새로운 아키텍쳐 소개
(GCN과 GraphSAGE와 비교)
🔹 Protein datasets
- enzyme인지 아닌지 분류하기
- 이 데이터셋은 이미 graph 형태로 인코딩되어 있음
(GraphSAGE에서처럼) 바로 GNN에 데이터를 적용하는 것이 아니라 훈련속도를 가속화해줄 mini-batching이 필요하다.
우리는 GIN이라는 아키텍쳐를 사용할 것이다.
🔹 GIN
목적: GNN의 discriminative(=representational) power 극대화
Weisfeiler-Lehman test를 사용해서 GNN의 power를 특성화할 수 있다.
- Isomorphic graphs는 두 그래프가 동일한 구조를 갖고 있을 때를 의미한다. (identical connections but a permutation of nodes)
- WL test는 두 그래프가 non-isomorphic인지만 알려줄 수 있다. (반대로 isomorphic한지는 보장하지 못한다.)
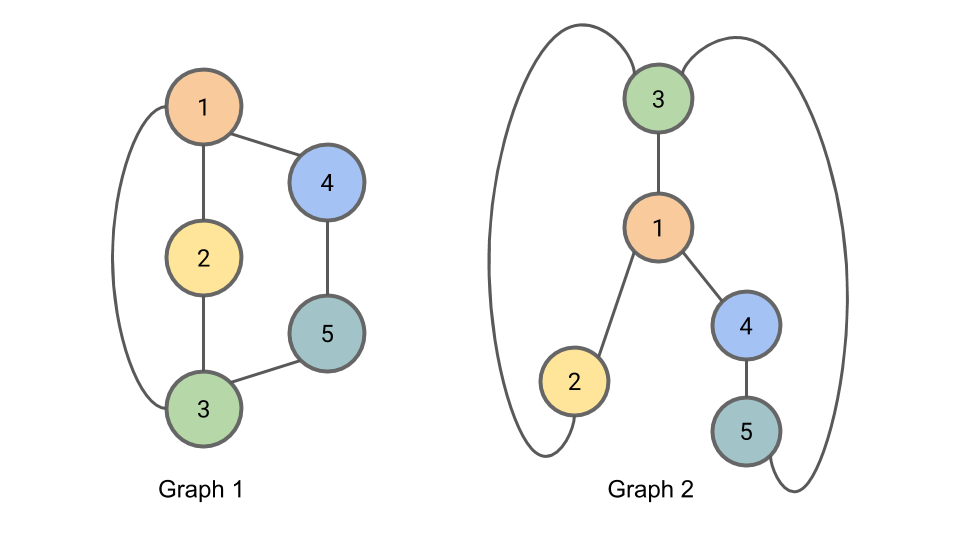
위 두 그래프는 isomorphic하다. correspondence를 표현하기 위해 노드별로 숫자, 색깔 표시해둔 것. 그러나, 이런 표시가 없다면? -> challenging problem
🔹 WL test와 GNN은 무슨 연관을 갖고 있나
비슷한 양상을 띤다.
1. 모든 node가 같은 label로 시작한다.
2. Labels from neighboring nodes are aggregated and hashed to produce a new label.
3. 앞 두 과정들 반복, until the labels stop changing.
이러한 WL test에 영감 받아 new aggregator를 디자인하게 되었다.
🔹 One aggregator to rule them all
이 새로운 aggregator는 non-isomorphic graph를 다룰 때 서로 다른 node embeddings를 만들어내야 한다.
👉 2개의 injective 함수를 사용하며, MLP를 통해 학습할 수 있다.
- With GINs, we learn the approximation of 2 injective functions. (universal approximation theorum에 따라)
특정 노드 i의 hidden vector를 GIN으로 계산하는 식은 다음과 같다.
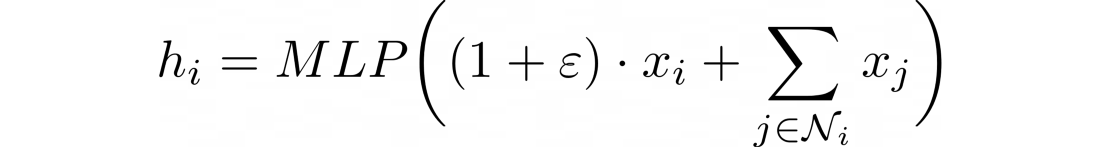
위 식에서 '입실론'은 target node의 중요도를 (compared to its neighbors) 결정한다. epsilon can be a learnable parameter or a fixed scalar.
🔹 Global Pooling (graph-level readout)
: GNN으로 계산된 node embeddings를 이용해서 graph embedding을 만들어내는 것
simple ways to obtain a graph embeddings
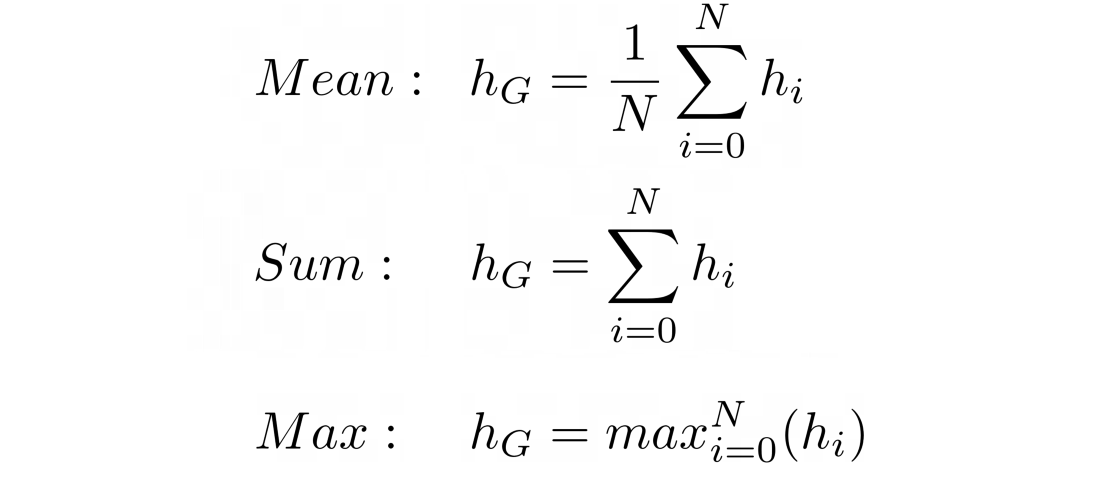
- 모든 structural information을 고려하려면 이전 layer의 임베딩을 잘 보존해야 한다.
- sum operator가 mean, max operator보다 more expressive
위와 같은 분석 결과로 아래와 같은 global pooling 식이 완성되었다.
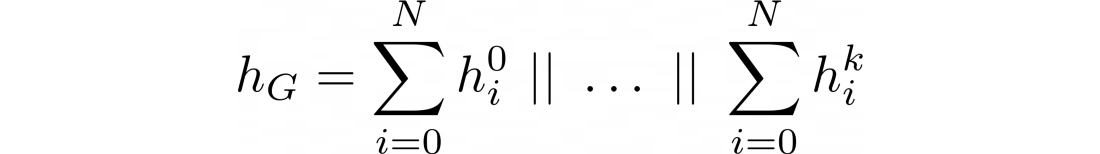
각 층마다 노드 임베딩은 합산되고 그 결과들이 concatenate(모든 결과 결합)된다. 이를 통해 sum operator의 expressiveness와, concatenation 이전의 iterations의 정보들(writer는 memory라 표현함)을 결합시킬 수 있다.
🔹 GIN in Pytorch Geometric
- GINConv (ɛ is entirely removed by default)
- GINEConv (neighbors' features에 ReLU 함수 적용)
GIN layer에 MLP 적용
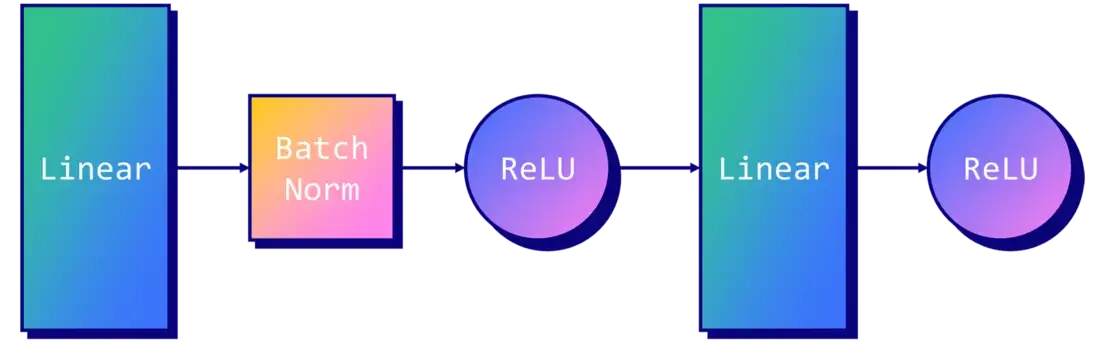
그렇다면 GIN의 architecture는
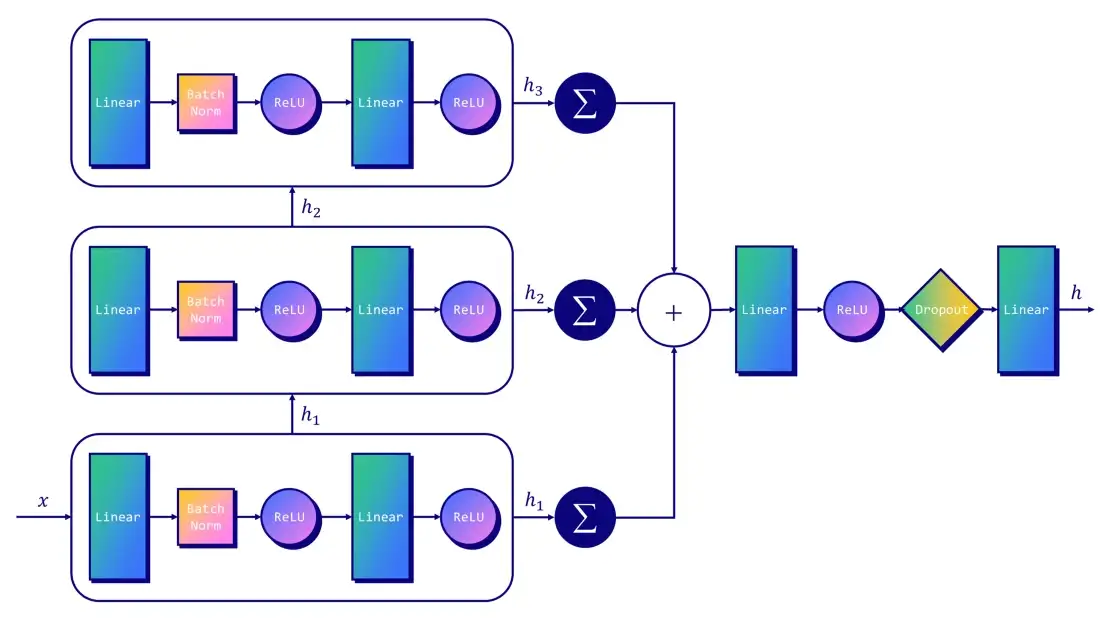
(images by author)
class GIN(torch.nn.Module):
"""GIN"""
def __init__(self, dim_h):
super(GIN, self).__init__()
self.conv1 = GINConv(
Sequential(Linear(dataset.num_node_features, dim_h),
BatchNorm1d(dim_h), ReLU(),
Linear(dim_h, dim_h), ReLU()))
self.conv2 = GINConv(
Sequential(Linear(dim_h, dim_h), BatchNorm1d(dim_h), ReLU(),
Linear(dim_h, dim_h), ReLU()))
self.conv3 = GINConv(
Sequential(Linear(dim_h, dim_h), BatchNorm1d(dim_h), ReLU(),
Linear(dim_h, dim_h), ReLU()))
self.lin1 = Linear(dim_h*3, dim_h*3)
self.lin2 = Linear(dim_h*3, dataset.num_classes)
def forward(self, x, edge_index, batch):
# Node embeddings
h1 = self.conv1(x, edge_index)
h2 = self.conv2(h1, edge_index)
h3 = self.conv3(h2, edge_index)
# Graph-level readout
h1 = global_add_pool(h1, batch)
h2 = global_add_pool(h2, batch)
h3 = global_add_pool(h3, batch)
# Concatenate graph embeddings
h = torch.cat((h1, h2, h3), dim=1)
# Classifier
h = self.lin1(h)
h = h.relu()
h = F.dropout(h, p=0.5, training=self.training)
h = self.lin2(h)
return h, F.log_softmax(h, dim=1)
gcn = GCN(dim_h=32)
gin = GIN(dim_h=32)
gcn = train(gcn, train_loader)
gin = train(gin, train_loader)위 코드는 실습코드의 일부이며 GIN과 GCN의 결과를 비교해본다.
정확도 면에서 GIN이 GCN을 훨씬 앞선다.
- GIN에서는 모든 층의 hidden vectors가 결합된다. (마지막 층만을 고려하는 것이 아니라)
- sum operator를 사용하는 GIN
Although GINs achieve good performance, especially with social graphs, their theoretical superiority doesn’t always translate well in the real world. It is true with other “provably powerful” architectures, which tend to underperform in practice, such as the 3WLGNN. -Author
