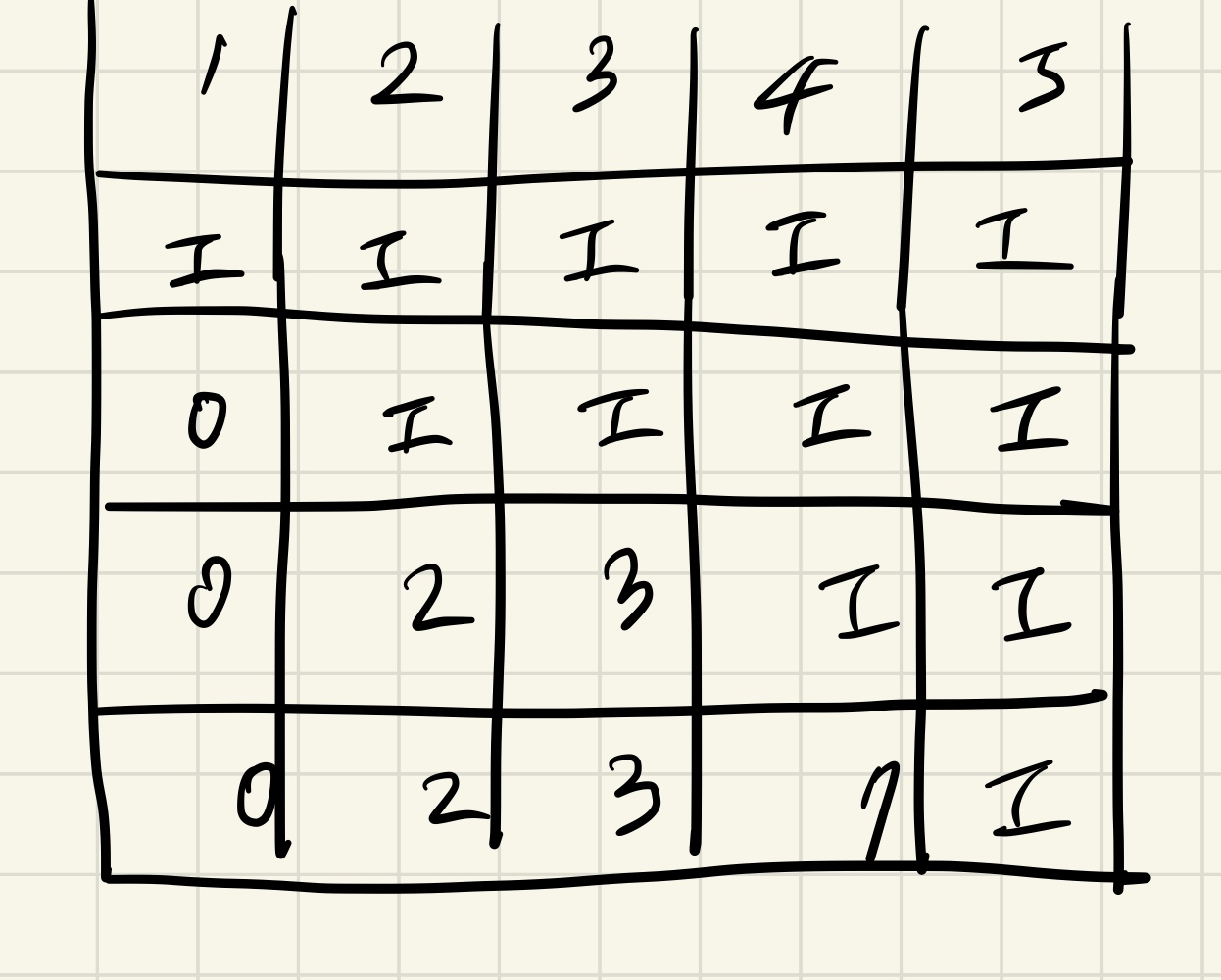
문제
https://www.acmicpc.net/problem/1753
소스코드
import sys
import heapq
sys.stdin = open("input.txt", 'r')
input = sys.stdin.readline
INF = sys.maxsize
if __name__ == "__main__":
v,e = map(int,input().split())
k = int(input())
graph = [[] for _ in range(v+1)]
for _ in range(e):
s,e,w = map(int,input().split())
graph[s].append((w,e)) #가중치 목적지 노드 형식으로 저장 > 우선순위 힙 사용하기 위해서
dp = [INF] *(v+1) #최소값을 업데이트 할 가중치 테이블
heap = [] #힙 -> 최소값을 구할 때 시간을 줄여주기 위한 자료구조
def dijkstra(start):
dp[start] = 0 #dp를 다 INF로 초기화 해놨으니 처음에 가중치를 0으로 세팅한다.
heapq.heappush(heap,(0,start)) #heap에 (가중치,도착점)으로 세팅한다 > 가중치로 최소힙 만들려고
while heap: #모든 정점을 체크해준다.
w,cur = heapq.heappop(heap) #가중치, 도착점
if dp[cur] < w: #현재 도착점에 누적된 값보다 가중치가 크면 그냥 pass
continue
for ww,vv in graph[cur]: #현재 도착점과 연결된 값을 체크해준다.
next_w = w + ww #시작점 ~ 도착점(w) ~ 새로운 도착점(ww) 으로 세팅하면 시작점에서 > 새로운 도착점으로 가는 방법이다.
if dp[vv] > next_w: #현재 도착점으로 가는 가중치과 하나 거쳐서 가는 가중치 비교
dp[vv] = next_w #더 작으면 변경하기 dp값 변경!
heapq.heappush(heap,(next_w ,vv)) #최소힙에 새로운 도착점과 가중치를 넣어서 탐색 대상으로 넣어준다.
dijkstra(k)
for i in range(1,v+1): #IF
print("INF" if dp[i]==INF else dp[i]) #이렇게 안해주면 sys.maxsize 9223372036854775807 출력됨설명
시작 정점에서 모든 정점으로 가는 최솟값 구하는 문제로 다익스트라 알고리즘!
그림으로 그리면 다음과 같다.
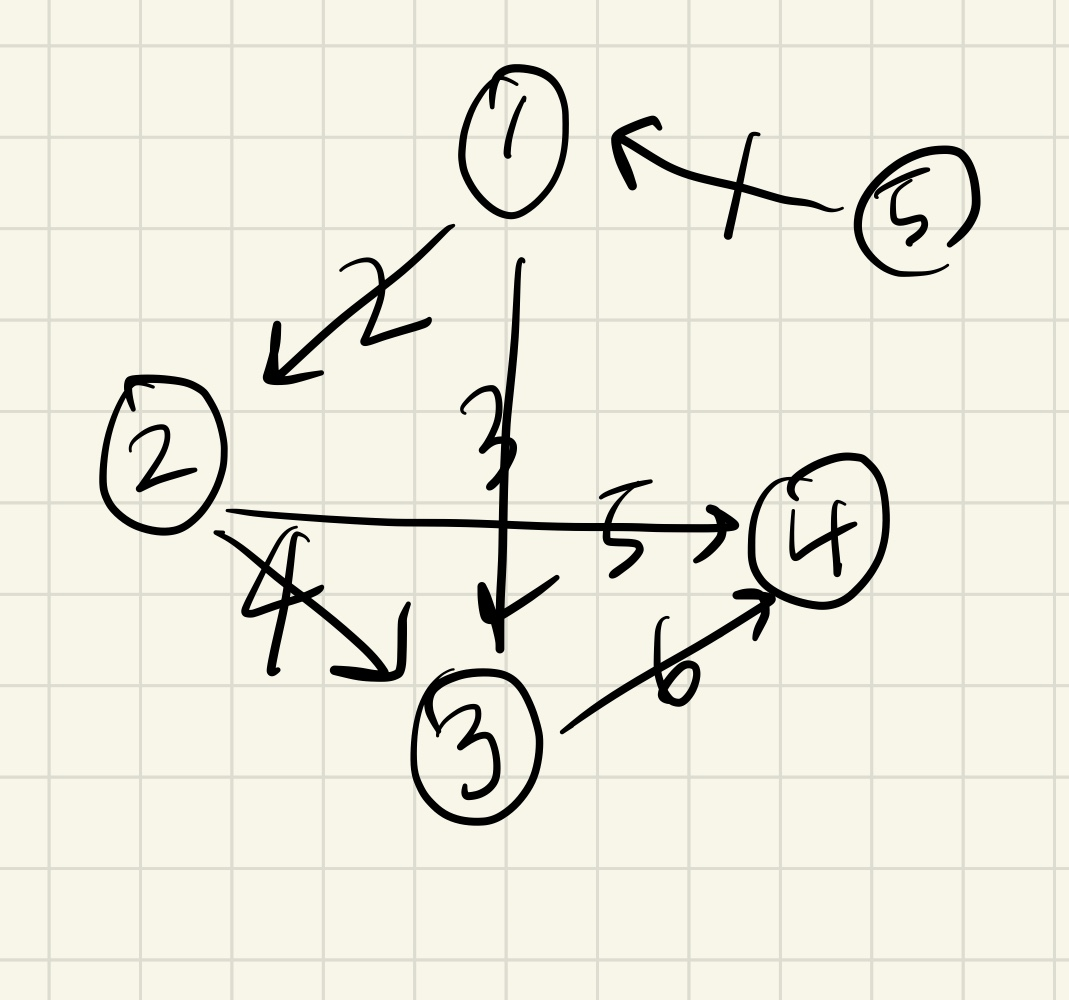

dp 배열이 최소값으로 변화하는 단계를 그림으로 표현하면 다음과 같다.