Big O

알고리즘의 시간, 공간복잡도를 표기하는 방법

---

Big o의 필요성

문제를 해결할 때 여러 방법이 있는데
여러가지 코드를 일반적으로 서로 비교하고 성능을 평가하기 위해 필요하다

---

시간복잡도

시간 복잡도(Time Complexity)는 알고리즘의 절대적인 실행 시간을 나타내는 것이 아닌 알고리즘을
수행하는 데 연산들이 몇 번 이루어지는 지를 숫자로 표기

---

Big o 개념 - 코드 시간 재기

내장 함수 performance.now();

함수를 실행하는데 얼만큼이 시간이 소요되었는지 확인

1 부터 n까지 수의 합을 구하는 함수 비교

• 일반적인 함수

function addUpTo(n) {
  let total = 0;
  for (let i = 1; i <= n; i++) {
    total += i;
  }
  return total;
}

var t1 = performance.now();
addUpTo(1000000000);
var t2 = performance.now();
console.log(`Time Elapsed: ${(t2 - t1) / 1000} seconds.`)

• 더 효율적인 함수

function addUpTo(n) {
  return n * (n + 1) / 2;
}

var time1 = performance.now();
addUpTo(1000000000);
var time2 = performance.now();
console.log(`Time Elapsed: ${(time2 - time1) / 1000} seconds.`)

---

연산 개수 세기

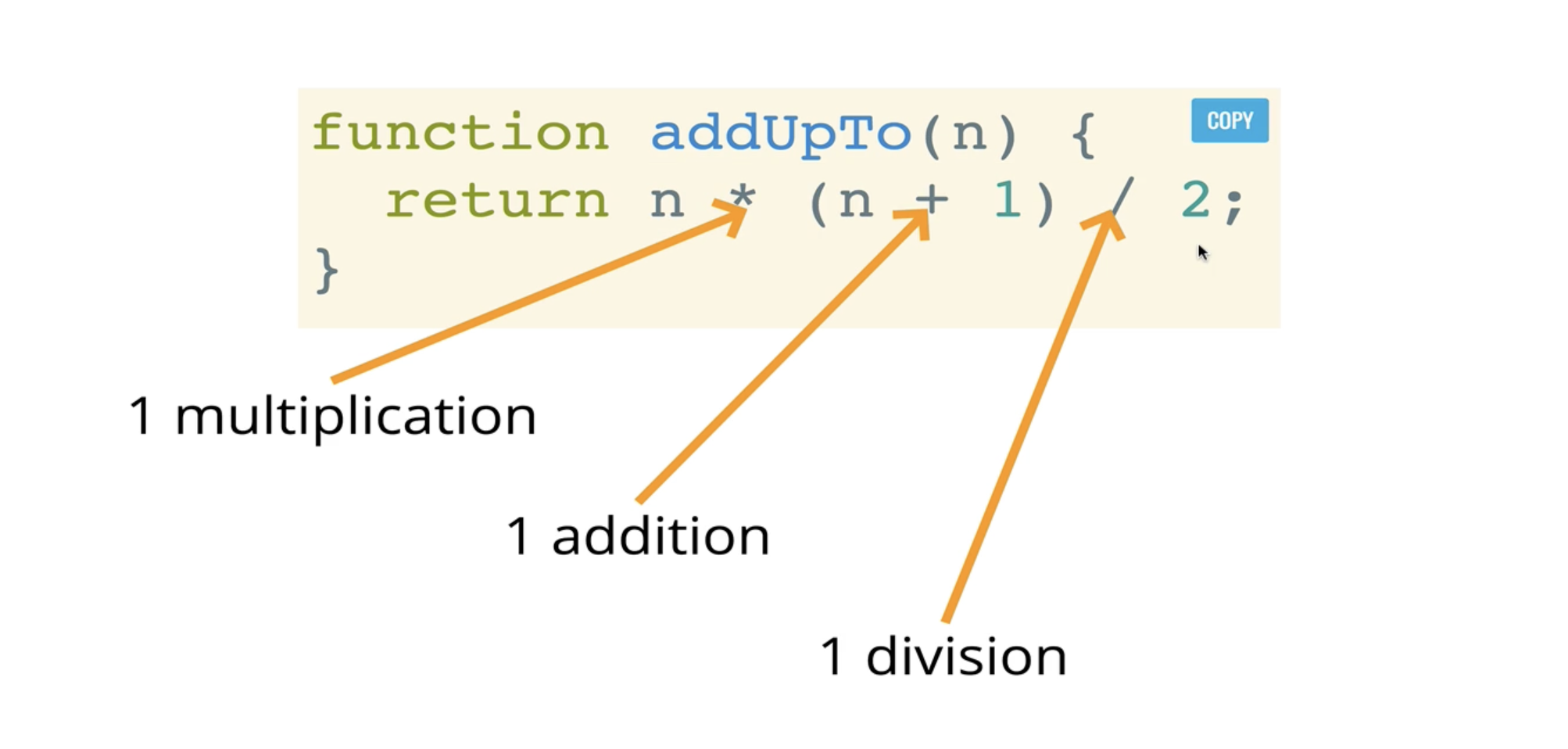
위 두 함수는 같은 결과를 도출하지만 연산의 횟수에서 차이가 발생합니다
연산 개수를 정확하게 세는 것이 중요한 것이 아니라
연산이 어느정도로 발생하는지 추세를 확인하는 용도로 Big O 표기법을 사용합니다

---

Big O 복잡도

O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(2^n)등의 순서로 복잡하다
단순한 알고리즘이 가장 효율적인 알고리즘이라고 할 수 있다.

ex)

n이 몇이든 항상 O(1) 시간복잡도를 가지는 함수

---

O(n) 시간복잡도를 가지는 함수

---

O(n^2) 시간복잡도를 가지는 함수

---

Big o 표기법 단순화

시간 복잡도 계산에 있어서 상수는 신경 쓰지않는다

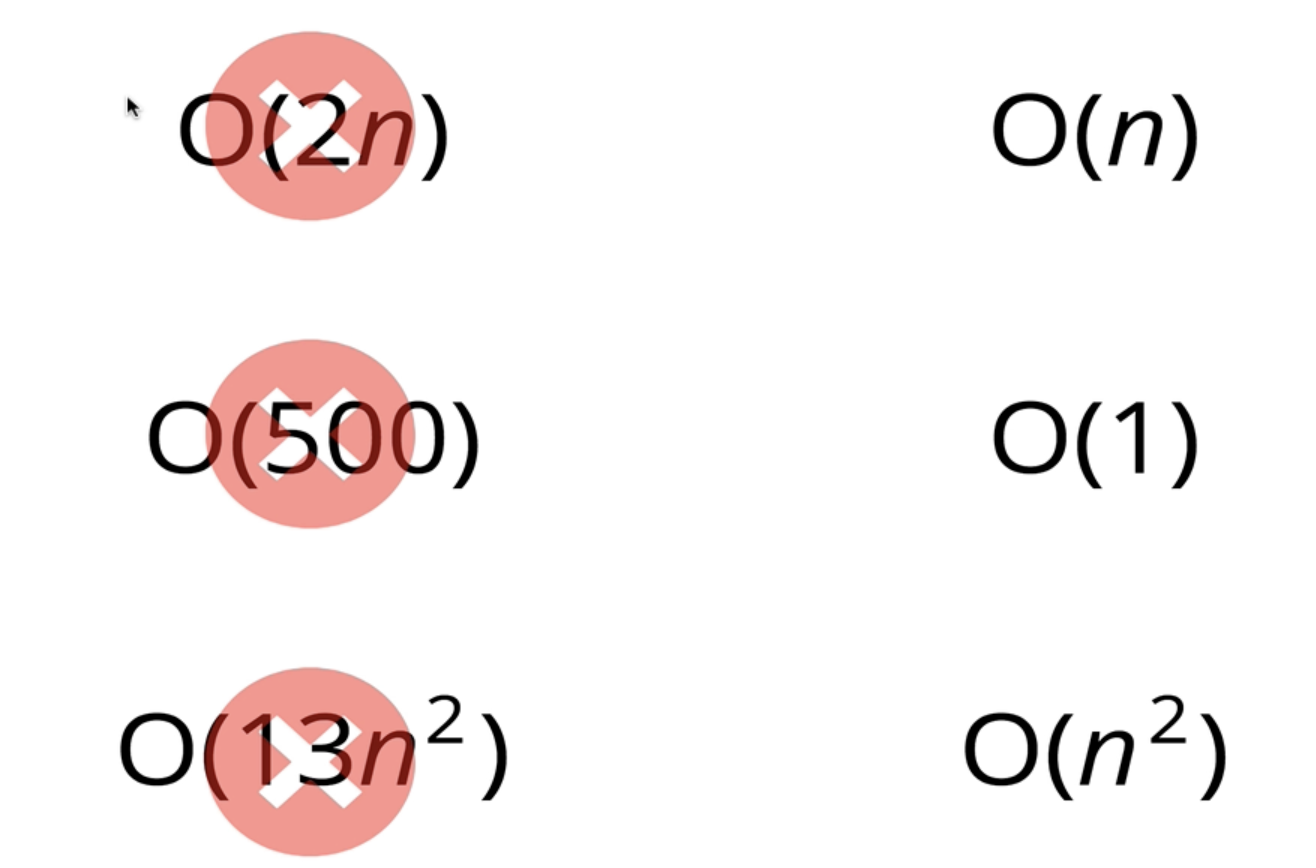
2n, 500, 13n^2 를 비교하는 것이 아닌 단순화한 n, 1, n^2을 가지고 시간복잡도를 비교한다.

1. 사칙연산(+, -, *, /) = 상수

2. 변수 할당 연산 = 상수

3. 인덱스를 이용해 배열 엘리먼트에 접근하는 연산 = 상수

4. 반복문 = n , 중첩 반복문일 경우 n * n

공간복잡도

**공간 복잡도(Space Complexity)란, 프로그램을 실행시킨 후 완료하는 데 필요로 하는 자원 공간의 양** - `boolean`, `numbers`, `undefined`, `null`은 자바스크립트에서 모두 불변한 공간 - 문자열 `Strings`의 경우 O(n) 공간이 필요 - 참조 타입 자료형 `array`, `object`의 경우 O(n) 공간이 필요

➡️ `total`, `i` 변수의 값만 바뀜, O(1) 공간복잡도를 가진다.

➡️ input으로 들어오는 `arr`값 만큼 공간복잡도를 가진다. 즉, O(n) 공간복잡도를 가짐

로그함수

**지수함수의 역함, 지수를 다른 방식으로 표현한 것**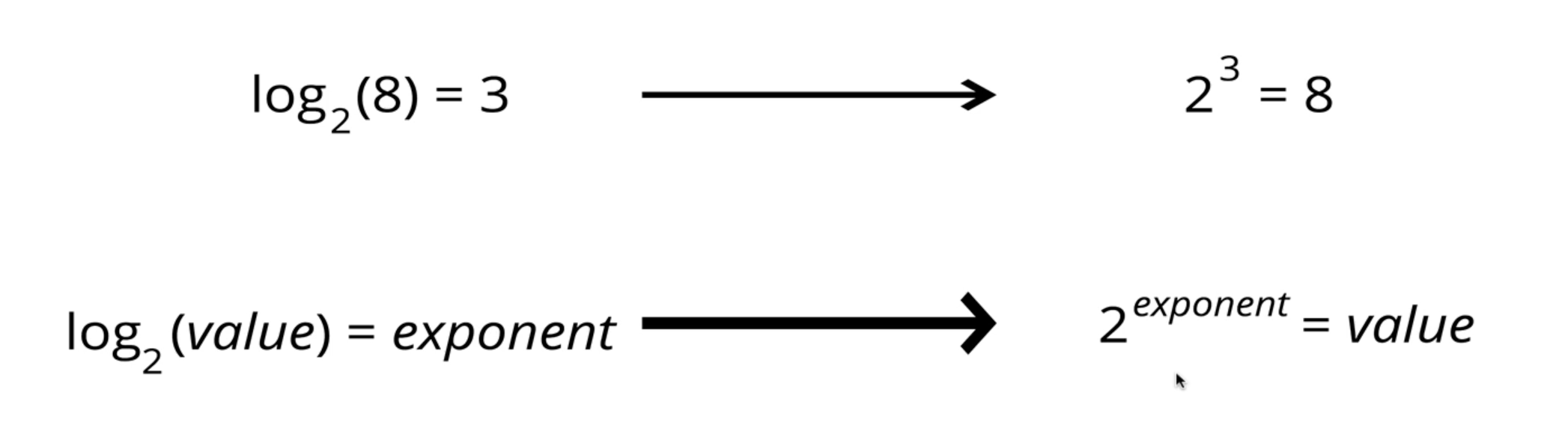 위 식을 쉽게 풀어서 설명하면 2를 밑으로 하는 어떤 값의 로그는 어떤 지수값과 같다고할 수 있다. 즉, `2`를 `exponent` 만큼 제곱한 값은 `value`이다.