개인공부-8

1. 유클리드 호제법

• 재귀함수 이용
• 최대 공약수 구하기

• A,B의 최대공약수 = > B%(A%B) == 0일 때를 구하면 된다.

public class Euclidean {

    int solution(int first, int second){


       if(first%second==0){
            System.out.println(first+ " "+ second);
            return second;
        }

        return solution(second,first%second);
    }


    public static void main(String[] args) {

        Euclidean ec = new Euclidean();
        System.out.println(ec.solution(1071,1029));
    }
}

• 예제 설명
  1071 % 1029 != 0 ( X )
  1029 % 42 != 0 ( X )
  42 % 21 == 0 ( O ) -> 이때의 B가 최대공약수

• 최소 공배수 구하기

public class Euclidean {

   static int solution(int first, int second){


       if(first%second==0){
            System.out.println(first+ " "+ second);
            return second;
        }

        return solution(second,first%second);
    }

   static int solution2(int first, int second){

       int num = solution(first, second);
        return (first/num) * (second/num) * num;
    }


    public static void main(String[] args) {

        System.out.println(solution(1071,1029));
        System.out.println(solution2(1071,1029));
    }
}

• 크게 다를건 없다.
• 최소공배수 => 주어진 두수를 최대 공약수로 나눈 것과 최대공약수의 곱

2. DP (동적 계획법 Dynamic Programming)

• 개념 : 큰 개념을 작은 개념으로 나누어서 푸는 개념
• ex : 피보나치 수열
  -> Fn = Fn-1 + Fn-2

• 재귀함수 방법( 시간 복잡도 O(2^n) )

public class Dp2 {

    static int fifo(int n){

        if(n==0) return 0;
        if(n==1) return 1;

        return fifo(n-1) + fifo(n-2) ;
    }

    public static void main(String[] args) {

        System.out.println(fifo(10)); // 55 
    }
}

• 재귀함수 + 메모이제이션 방법 ( 시간 복잡도 O(N) )

package org.example.level1;

public class Dp2 {

    static int fifo(int n){

        int [] memo = new int[1001];
        if(n<=1) return n;
        if(memo[n]!=0) return memo[n];
        memo[n] = fifo(n-1) + fifo(n-2);
        return (fifo(n-1) + fifo(n-2)) % 1000000;
    }

    public static void main(String[] args) {

        System.out.println(fifo(10));
    }
}

• 피사노 주기
• 피보나치 수를 K로 나눴다고 했을 때, 그 나머지는 항상 주기를 가지게 되는데 이를 피사노 주기라 함.
• 출처 : https://lms0806.tistory.com/72

package org.example.level1;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Dp2 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int pisano = 1500000;
        long size = Long.parseLong(br.readLine()) % pisano;

        long[] num = new long[pisano + 1];

        num[0] = 0;
        num[1] = 1;

        for(int i = 2; i <= pisano; i++) {
            num[i] = (num[i - 1] + num[i - 2]) % 1000000;
        }

        System.out.print(num[(int)size]);
    }
}

package org.example.level1;

public class Dp2 {
    public static final int p = 1500000;
    static int fifo(int n){


        int [] memo = new int[p+1];
        memo[0] = 0;
        memo[1] = 1;

        for(int i =2 ; i <= p ; i ++){
            memo[i] = (memo[i-1] + memo[i-2]) % 1000000;
        }
        return memo[n%p];
    }

    public static void main(String[] args) {

        System.out.println(fifo(1000));
    }
}

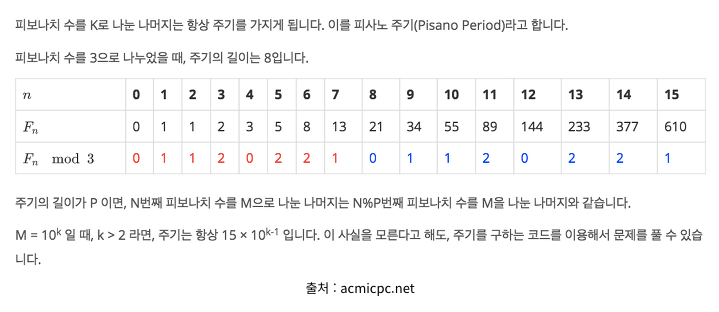
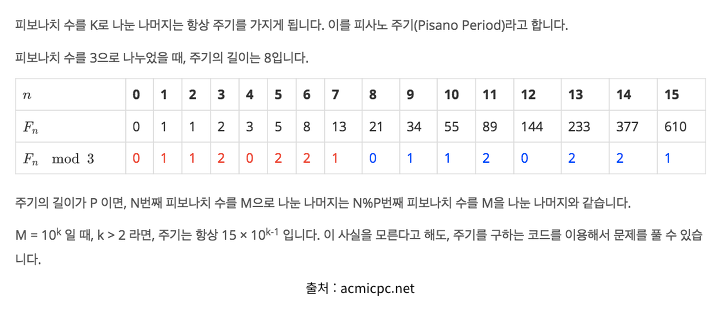
• 사실 정확한 원리 까지는 아직 잘 이해하지 못했다.
• 문제를 풀 때 적용한 개념은 피사노 주기로써,
  나누는 수( Mod ) N >=10 일때 , 주기는 = 15 * 10 ^ N-1 이라는 개념을 사용했다.
• 1000000을 나눈 나머지를 한다는 가정하에 1500000번을 주기로 똑같은 값이 주어진다.