최대공약수
공약수 : 두개 이상의 숫자에 대해 공통된 약수
최대공약수 : 공약수 중 가장 큰 약수
예제
문제: 최대공약수 구하기
두 수를 입력받아서 그 두 수의 최대공약수를 계산하는 프로그램을 작성하세요.
입력:
첫 번째 수를 입력하세요: [첫 번째 수 입력]
두 번째 수를 입력하세요: [두 번째 수 입력]
출력:
[첫 번째 수]와 [두 번째 수]의 최대공약수는 [최대공약수]입니다.
from math import *
a = int(input('첫 번째 수를 입력하세요:' ))
b = int(input('두 번째 수를 입력하세요:' ))
result_list = []
for i in range(1, min(a, b)+1) :
if a % i == 0 and b % i == 0 :
result_list.append(i)
result = max(result_list)
print(f'{a}와 {b}의 최대공약수는 {result}입니다.')최소공배수
공배수 : 두개 이상의 수에서 공통된 배수
최소공배수 : 공배수 중 가장 작은 수
예제
두 개의 자연수를 입력받아서 그 두 수의 최소공배수를 출력하는 프로그램을 작성하세요.
num1 = int(input('첫 번째 수를 입력하세요:' ))
num2 = int(input('두 번째 수를 입력하세요:' ))
def gcd(a, b):
while b:
a, b = b, a%b
return a
def lcm(a,b) :
return (a*b)//cal(a,b)
result = lcm(num1,num2)
print(f'{num1}와 {num2}의 최소공배수는 {result}입니다.')최대 공배수 구하는 함수가 레전드 어렵네잉
gcd(a, b):
while b:
a, b = b, a%b
return a
이 함수가 최대 공약수 구하는 함수래
해당 부분은 유클리드 호제법 알고리즘의 핵심 부분입니다. 유클리드 호제법은 두 수의 최대공약수를 구하는 알고리즘 중 하나로, 두 수의 나머지를 이용하여 최대공약수를 찾아냅니다.
설명을 간단히 드리면 다음과 같습니다.
두 수 a와 b를 입력받습니다.
b가 0이 될 때까지 반복합니다.
a를 b로 나눈 나머지를 구하고, 그 값을 a에 대입합니다.
b를 이전의 a로 대입합니다.
b가 0이 될 때까지 위 과정을 반복합니다.
반복이 종료되었을 때 a의 값이 최대공약수가 됩니다.
이렇게 유클리드 호제법을 통해 최대공약수를 구하는 것이 위 코드에서 해당 부분의 역할입니다. 즉, 두 수의 최대공약수를 구하기 위해 반복적으로 두 수를 나누고 나머지를 구하며 값을 업데이트하는 과정을 진행하게 됩니다. 반복이 종료되면 a에는 최대공약수가 저장되어 반환됩니다.
그 함수를 이용해서
def lcm(a,b) :
return (a*b)//cal(a,b)
이런 최대 공배수 함수를 구할 수 있다...
예제
두 사람이 함께 음악을 연주하는데, 한 사람은 10분마다 한 곡을 연주하고, 다른 사람은 15분마다 한 곡을 연주합니다. 두 사람이 처음으로 동시에 곡을 연주하는 시간을 구하는 프로그램을 작성해보세요.
from math import *
a = 10
b = 15
def gcl(num1, num2) :
while num2 :
num1, num2 = num2, num1%num2
return num1
def lcm (num1, num2) :
return (num1 * num2) // gcl(num1, num2)
result = lcm(a,b)
print(f'두 사람이 처음으로 동시에 곡을 연주하는 시간은 {result}분 뒤이다.')진법
생활에서 사용하는 10진법 외에 프로그램에서 사용하는 다양한 진법들
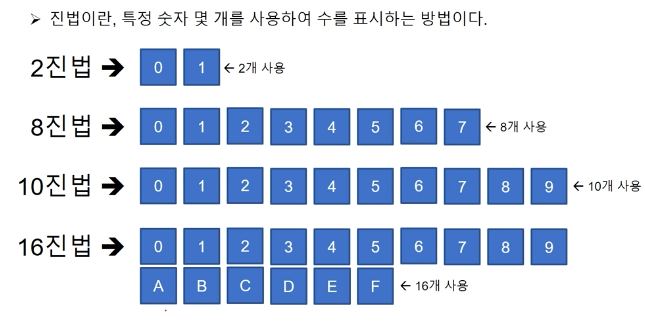




예제
주어진 10진수 정수를 원하는 진법으로 변환하는 프로그램을 작성해보세요.
세부 사항:
사용자로부터 10진수 정수를 입력받습니다.
사용자로부터 목표로 하는 진법을 입력받습니다.
입력된 정수를 목표 진법으로 변환하여 출력합니다.
변환 결과는 문자열 형태로 출력합니다.
진법은 2, 8, 16 범위를 지원합니다.
dNum = int(input('10진수 정수를 입력하세요'))
want = int(input('목표로 하는 진법을 입력하세요 (2,8,16)'))
if want == 2 :
print('{}을 {}진법으로 변환하면 {}입니다.'.format(dNum, want, format(dNum, '#b')))
elif want == 8 :
print('{}을 {}진법으로 변환하면 {}입니다.'.format(dNum, want, format(dNum, '#o')))
elif want == 16 :
print('{}을 {}진법으로 변환하면 {}입니다.'.format(dNum, want, format(dNum, '#x')))
수열
나열된 수의 규칙
특정항은 특정항까지의 합에서 특정항 이전의 항까지의 합을 뺀것과 같다.
등차수열
연속된 두 항의 차이가 일정한 수열
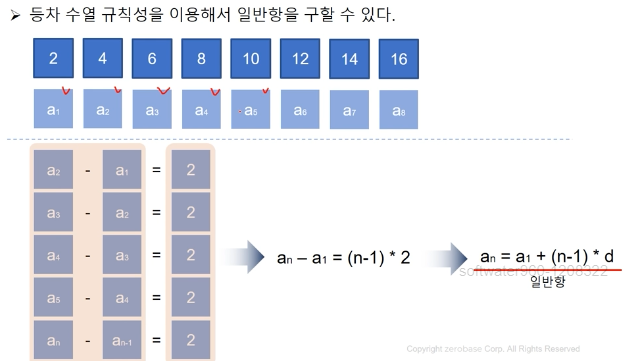
등차수열과 일반항
등차수열 규칙성을 이용해서 일반항을 구할 수 있다.
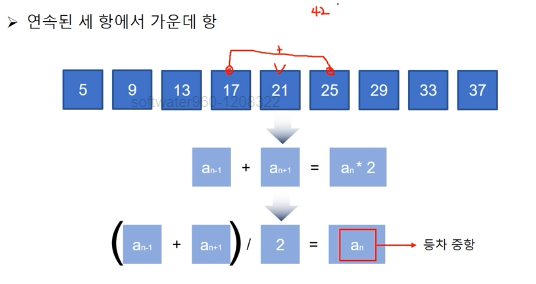
등차중항
연속된 세항에서 가운데항
등차수열의 합
규칙성을 이용해서 모든 항들의 총합을 구할 수 있다.

쩝
여기서 이해 불가
예제
주어진 시작 값(start), 등차(difference), 항의 개수(count)에 대해 등차수열의 합을 구하는 파이썬 코드를 작성하세요.
start = int(input('시작 값'))
difference = int(input('등차'))
count = int(input('항의 개수'))
n =start + ((count-1) * difference)
sumN = count* (start+n) / 2
print(f'주어진 시작 값(start), 등차(difference), 항의 개수(count)에 대해 등차수열의 합 : {sumN}')아이참
파이썬 내부에는 등차수열의 일반항이나 합에 대한 공식은 없으니.. 외워야함
흑
일반항 =start + ((count-1) * difference)
등차수열의 n번항 까지의 합 = count* (start+일반항공식(n)) / 2
예제
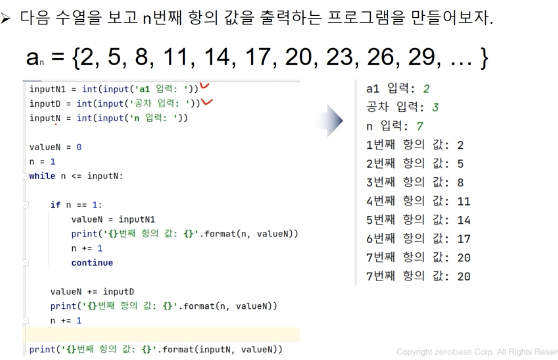
start = int(input('시작 값'))
difference = int(input('등차'))
count = int(input('항의 개수'))
def cal(start, n, difference):
result = start + ((n-1)* difference)
return result
num = 1
while num <= count :
result = cal(start, num, difference)
print(f'{num}번째 항의 값 : {result}')
num += 1
continue예제

start = int(input('시작 값'))
difference = int(input('등차'))
count = int(input('항의 개수'))
def cal(start, n, difference):
result = start + ((n-1)* difference)
return result
def sumCal(start, n):
result = n*(start+cal(start, n, difference))/2
return result
num = 1
while num <= count :
result = sumCal(start, num)
print(f'{num}번째 항의 값 : {result}')
num += 1
continue