Basic of Regression
일반적인 문제 해결 절차
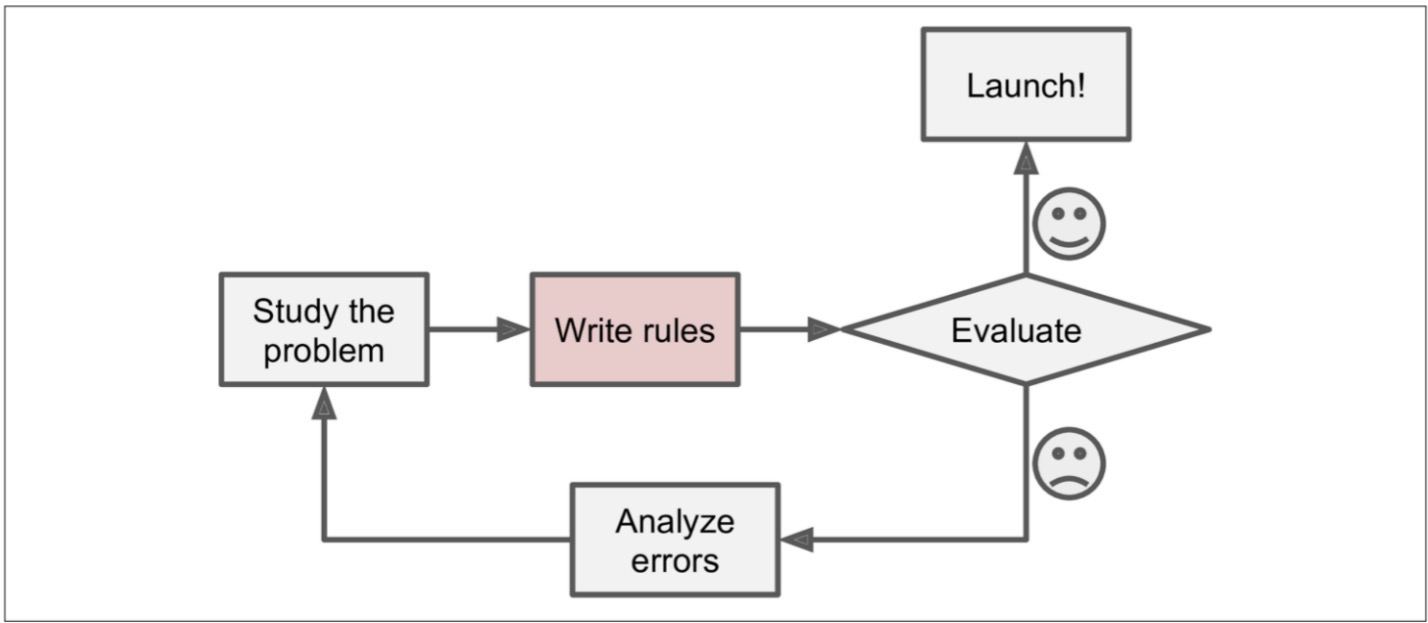
문제에 대해 공부하고,
해결책을 실제로 구체화하고 실행 가능한 형태로 만들어보며
선택한 해결책이나 접근 방식이 실제로 얼마나 효과적인지를 평가하고 개선한다음
런칭하거나 에러를 분석하여 재접근 한다.
만약, 데이터를 기반으로 한다면?
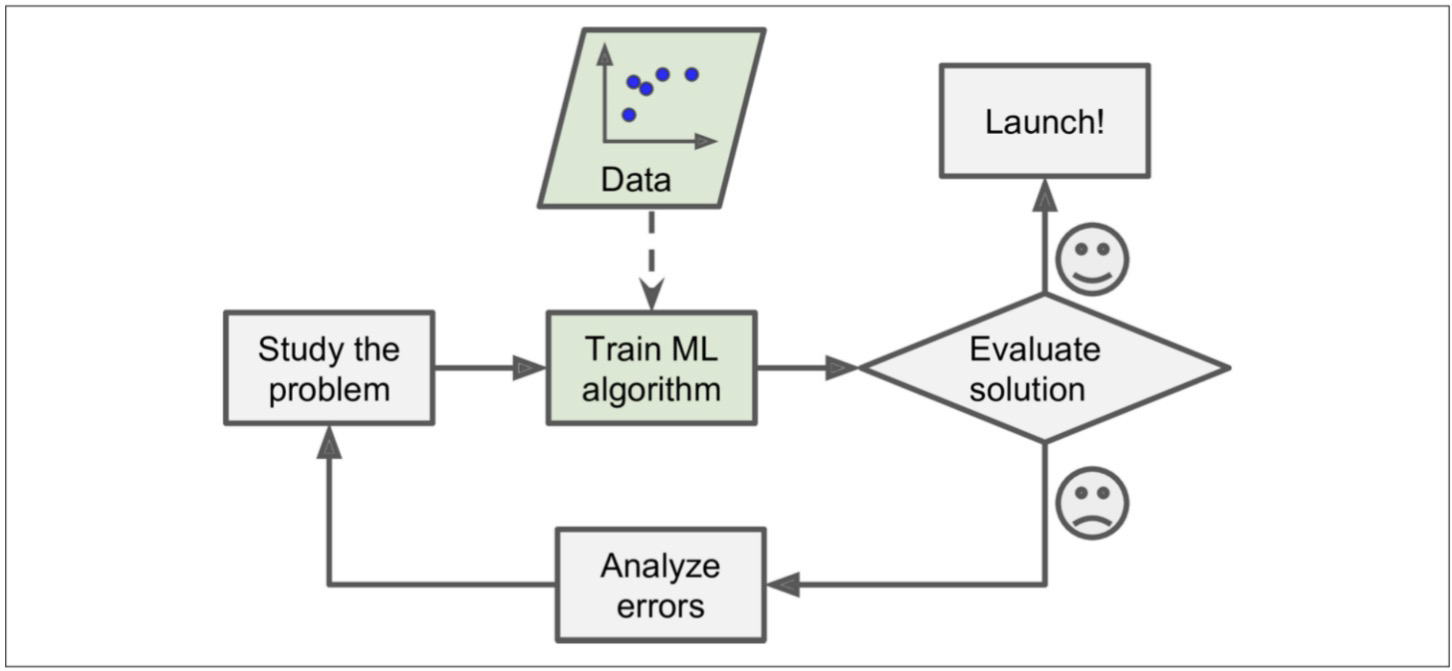
문제에 대해 공부한다음
데이터를 바탕으로 파악한 내용을 통해 머신러닝알고리즘에 학습을 시키고
머신러닝으로 도출된 방향성을 통해 정확도가 높으면 그를 바탕으로 런칭시키고, 정확도가 낮거나 신뢰도가 낮다면 이를 분석하여 재정립하여야 한다.
이에 더 나아가, 머신러닝 모델(알고리즘) 스스로 데이터를 기반으로 변화에 대응할 수 있다.
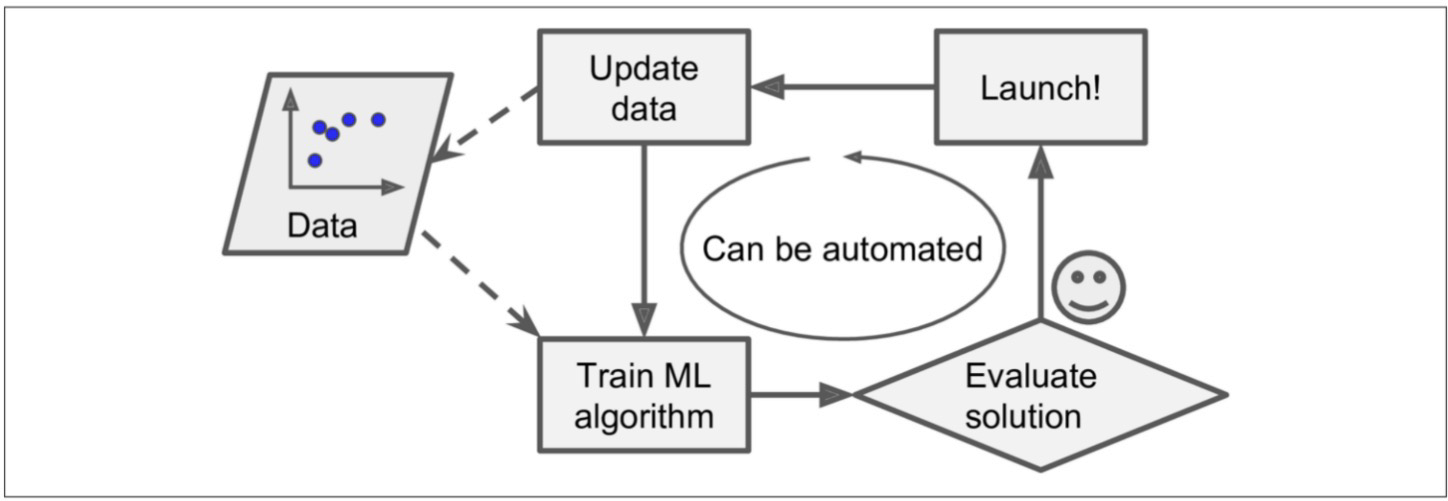
데이터로 머신러닝 알고리즘이 학습된다음
방향성 정확도, 신뢰도를 파악한다음
런칭시켰다가
새로운 데이터가 생기면 재학습하여 정확도 및 신뢰도를 업데이트하여 런칭하는
순환이 돌아가는 것이다.
심지어, 머신러닝을 통해 우리가 배울 수도 있다.
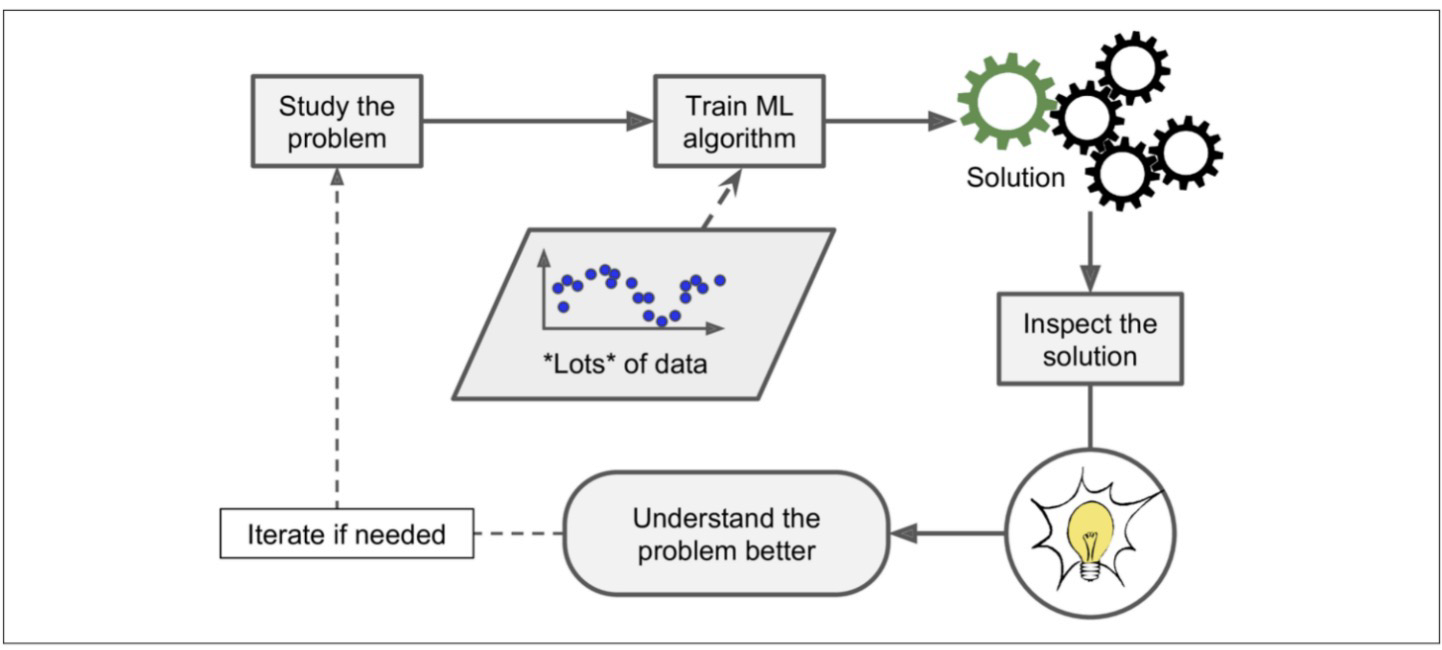
문제를 공부하고,
이를 바탕으로 적합한 다량의 데이터를 머신러닝 알고리즘에 학습시킨다음,
해결책이 도출되면 그를 바탕으로 문제를 깊게 이해하고, 더 나은 해결책을 도출한다.
그 후 필요에 의하면 본 과정을 반복한다.
지도학습 - 회귀 Regression
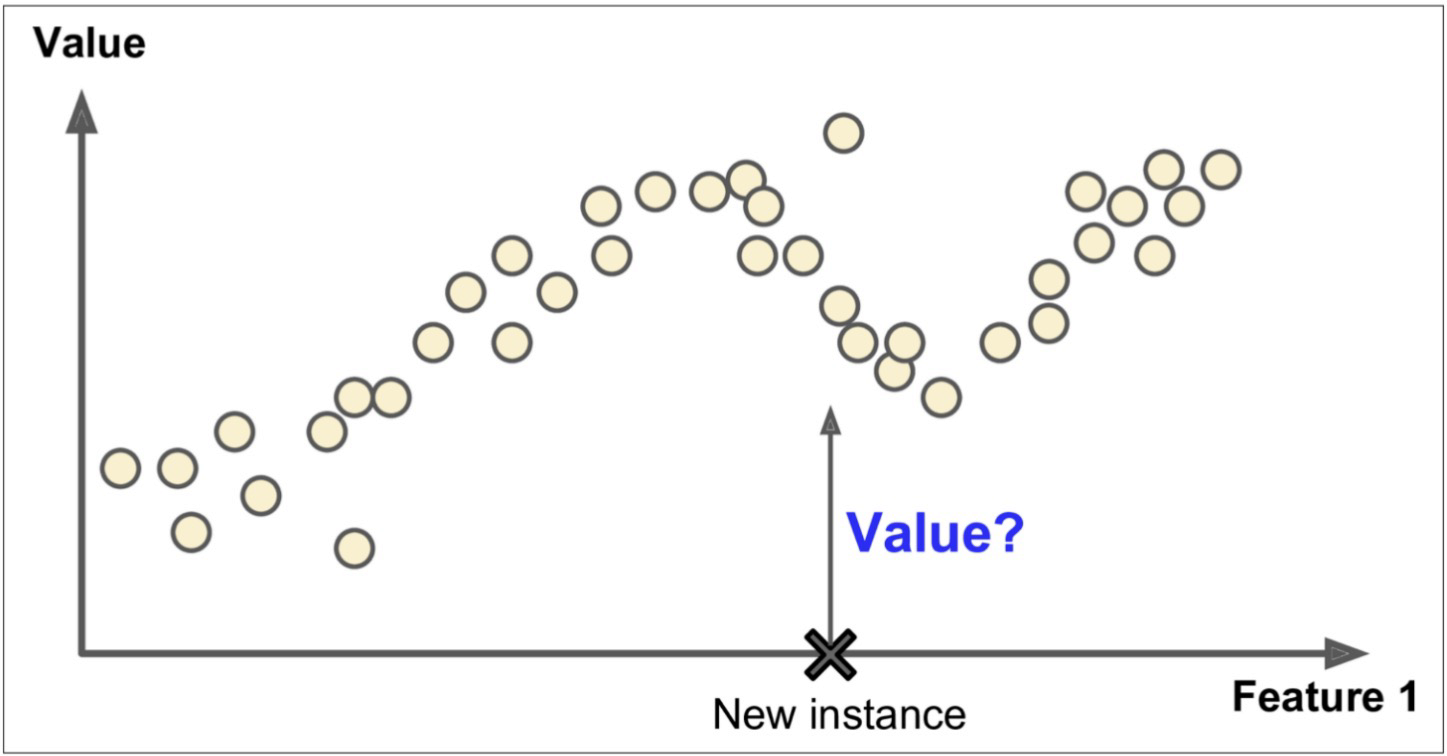
회귀는 주어진 입력 변수에 기반하여 출력 값을 예측하는 모델을 구축
지도학습-회귀의 특징
1. 연속적인 출력:
회귀 모델은 연속적인 출력 변수를 예측하는 데 사용됩니다. 예를 들어, 주택 가격, 온도, 판매량 등과 같은 연속적인 값을 예측할 때 사용됩니다.
random data를 통해 값을 예측하는 것이 아니라,
시간 순, 흐름에 따라 축적된 데이터의 그 다음데이터를 예측하는 것?2. 입력 변수와 출력 변수 간의 관계 모델링:
회귀는 입력 변수(또는 특성)와 출력 변수 간의 관계를 모델링하려고 합니다. 이 관계를 통해 입력 변수의 변화가 출력 변수에 어떤 영향을 미치는지 이해할 수 있습니다.
3. 학습 데이터를 통한 모델 훈련:
회귀 모델은 학습 데이터를 기반으로 학습되며, 데이터의 패턴과 관계를 학습하여 최적의 모델 파라미터를 찾습니다.
3. 손실 함수 최소화:
회귀 모델은 일반적으로 손실 함수를 정의하고 이 함수를 최소화하는 방향으로 학습합니다. 손실 함수는 예측값과 실제값의 차이를 측정하며, 이를 최소화하여 예측 성능을 향상시킵니다.
4. 다양한 알고리즘 사용 가능:
회귀 모델링에는 다양한 알고리즘이 사용될 수 있습니다. 선형 회귀, 다항 회귀, 서포트 벡터 머신(SVM), 결정 트리, 랜덤 포레스트, 신경망 등이 널리 사용되는 알고리즘입니다.
회귀 모델링의 단계
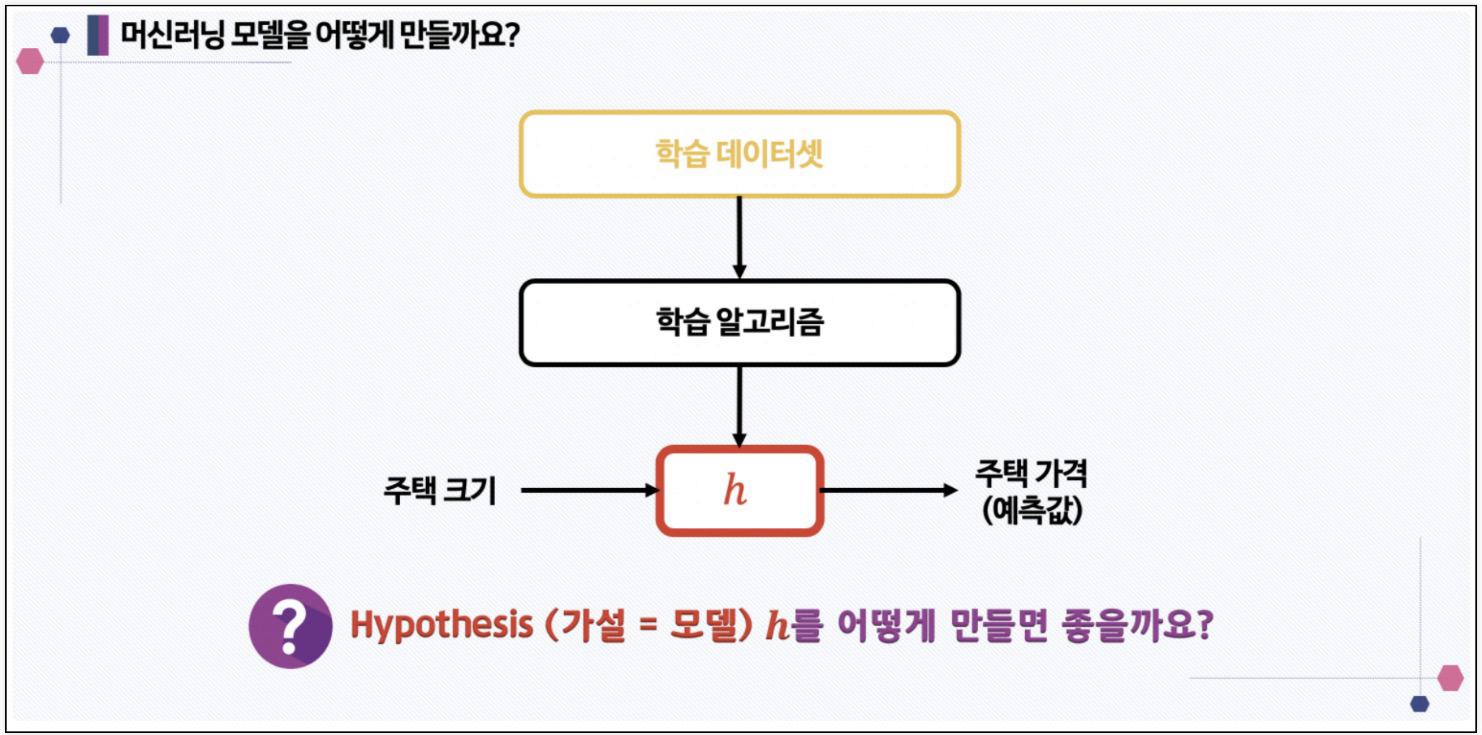
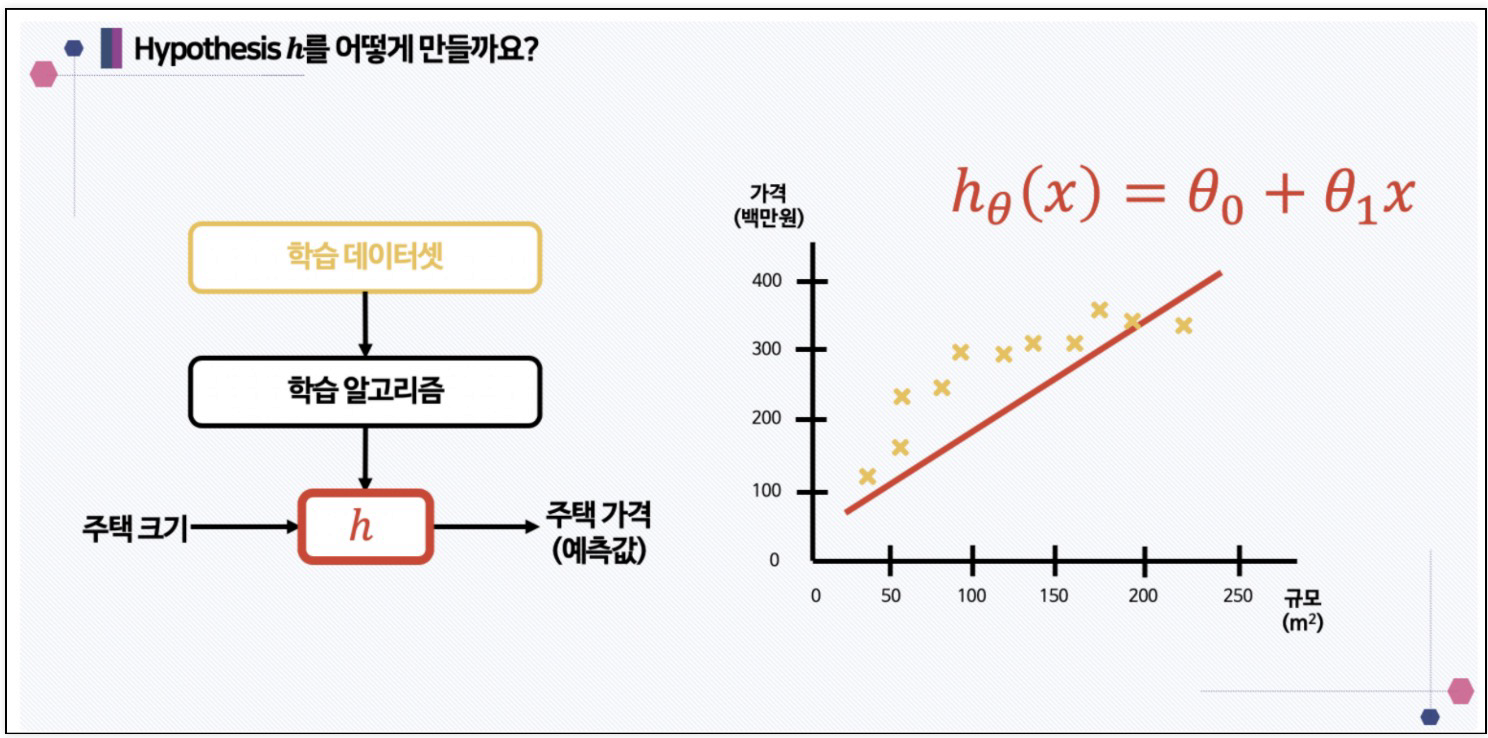
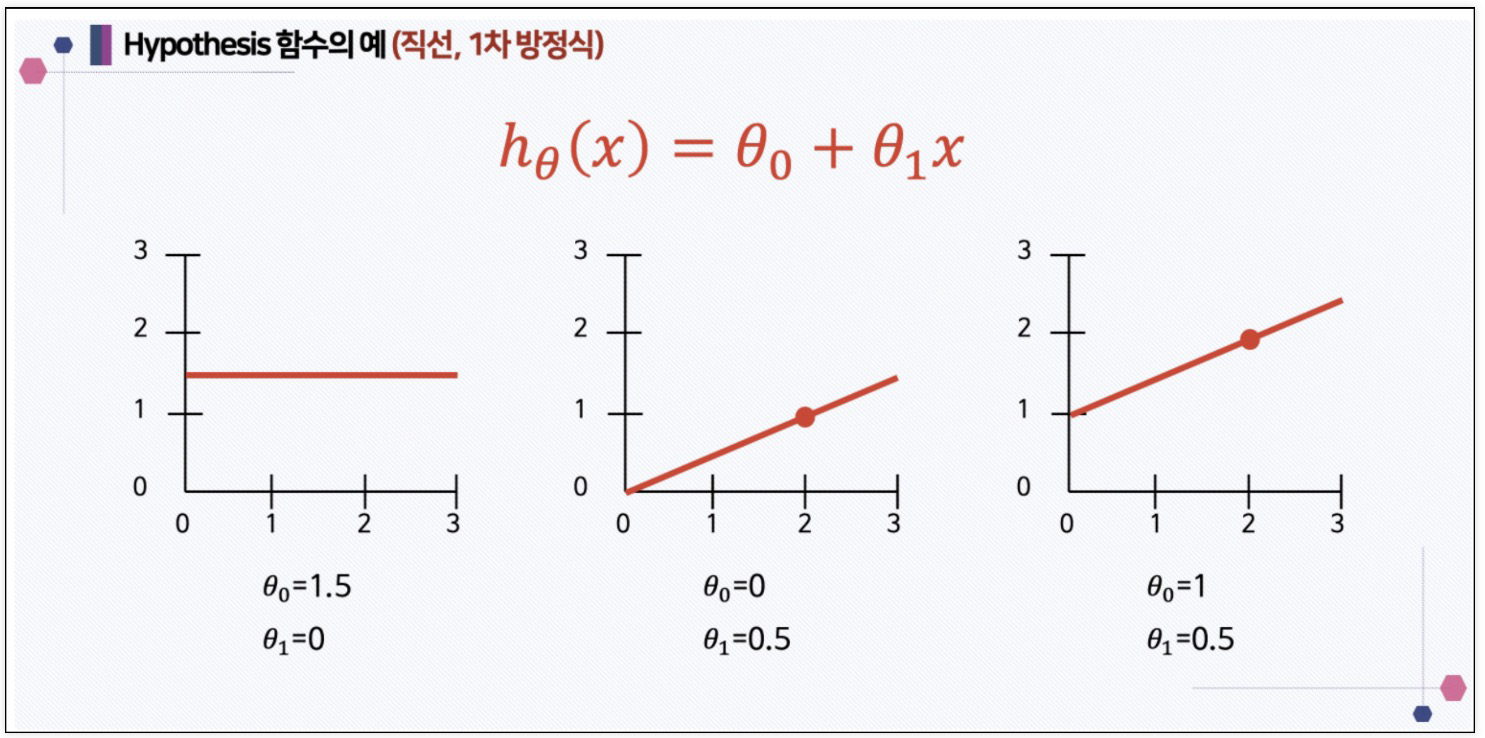
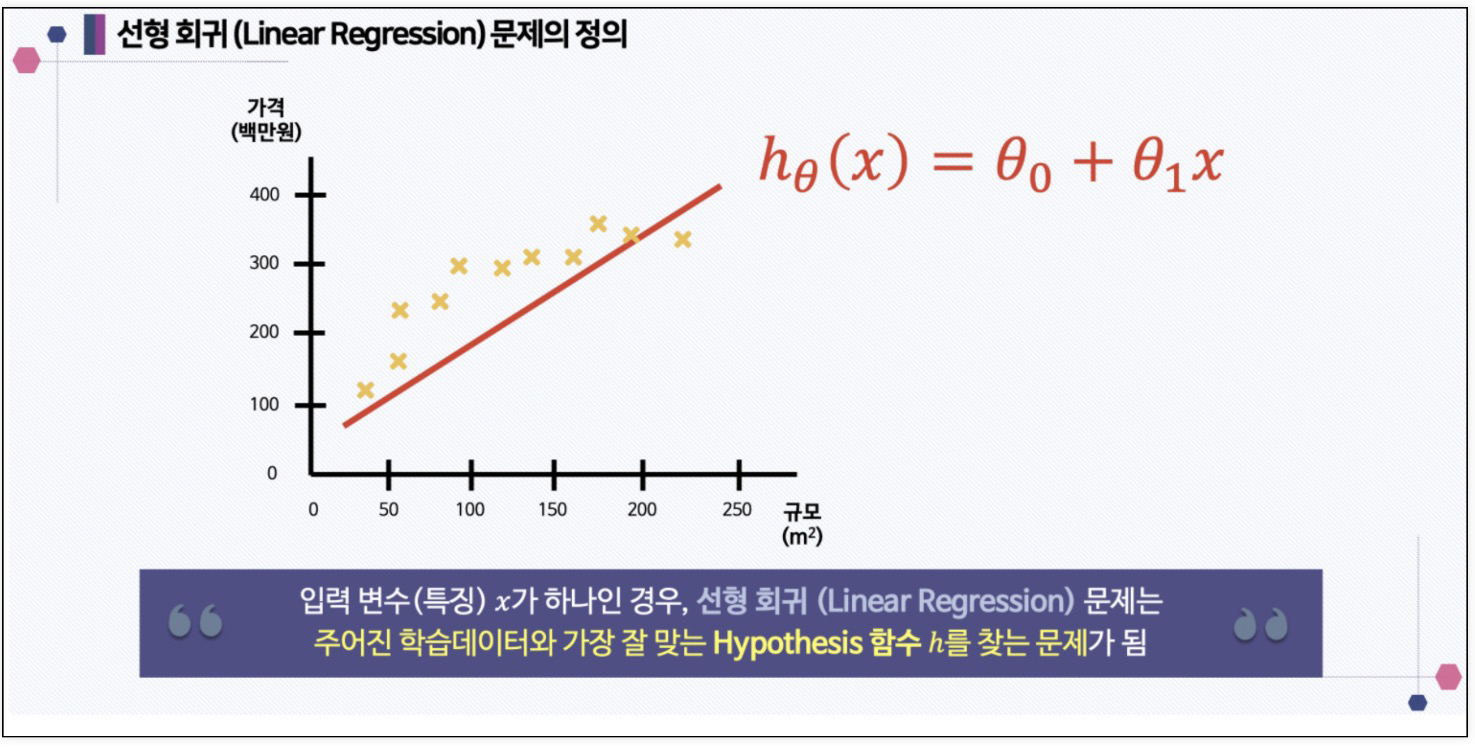
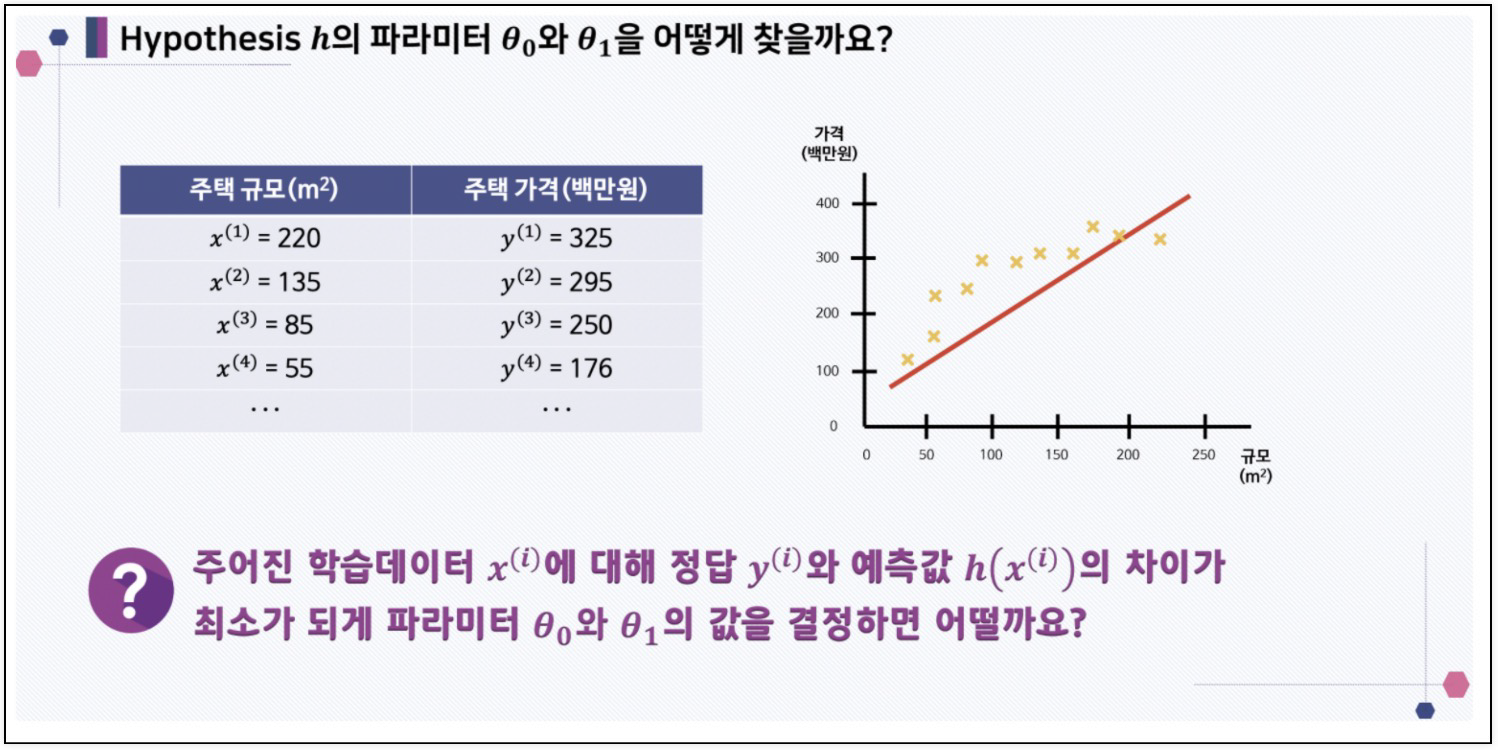
1. 데이터 수집:
입력 변수와 출력 변수를 포함한 학습 데이터를 수집합니다.
2.데이터 전처리:
데이터를 정제하고 필요한 형태로 가공합니다. 결측치 처리, 특성 스케일링, 범주형 변수 변환 등이 이에 해당합니다.
3. 모델 선택:
회귀 알고리즘 중에서 적절한 모델을 선택합니다. 데이터의 특성에 따라 다른 알고리즘이 적합할 수 있습니다.
4. 모델 훈련:
선택한 모델을 학습 데이터에 적용하여 모델 파라미터를 조정하고 학습합니다.
5. 모델 평가:
모델을 테스트 데이터에 적용하여 예측 성능을 평가합니다. 평가 지표로는 평균 제곱 오차(Mean Squared Error), R-squared 값 등이 사용됩니다.
6. 예측:
훈련된 모델을 사용하여 새로운 입력 데이터에 대한 출력 값을 예측합니다.
즉, 회귀는 예측 분석, 경제학, 생명 과학, 기상학 등 다양한 분야에서 활용되며, 입력 변수와 출력 변수 간의 관계를 이해하고 예측하는 데에 중요한 도구입니다.
데이터에 대한 가설 세우기

데이터 시각화
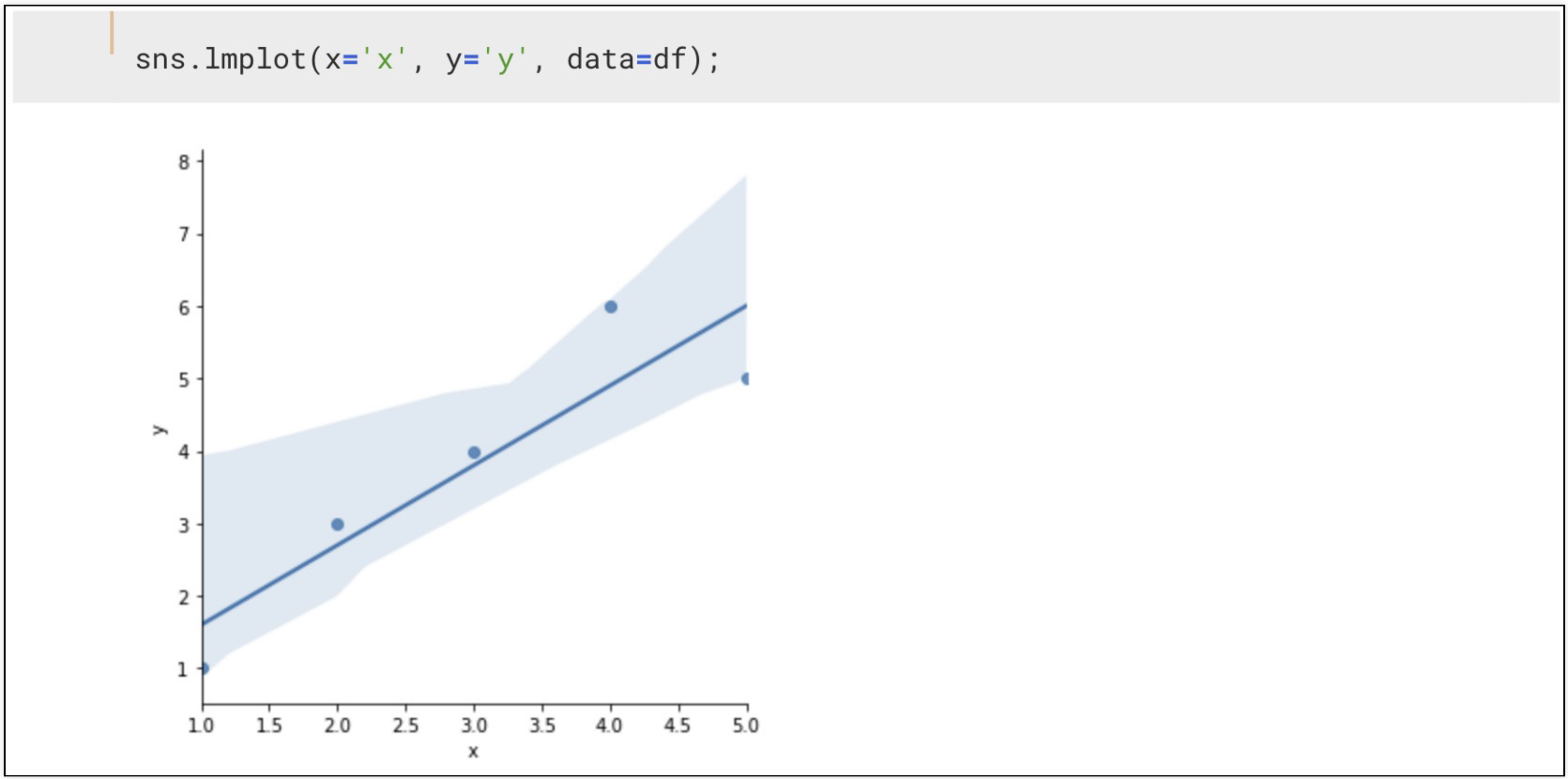
잔차평가 residue
잔차는 평균이 0인 정규분포를 따르는 것.
잔차평가는 잔차의 평균이 0 이고 정규 분포를 따르는지 확인
잔차확인
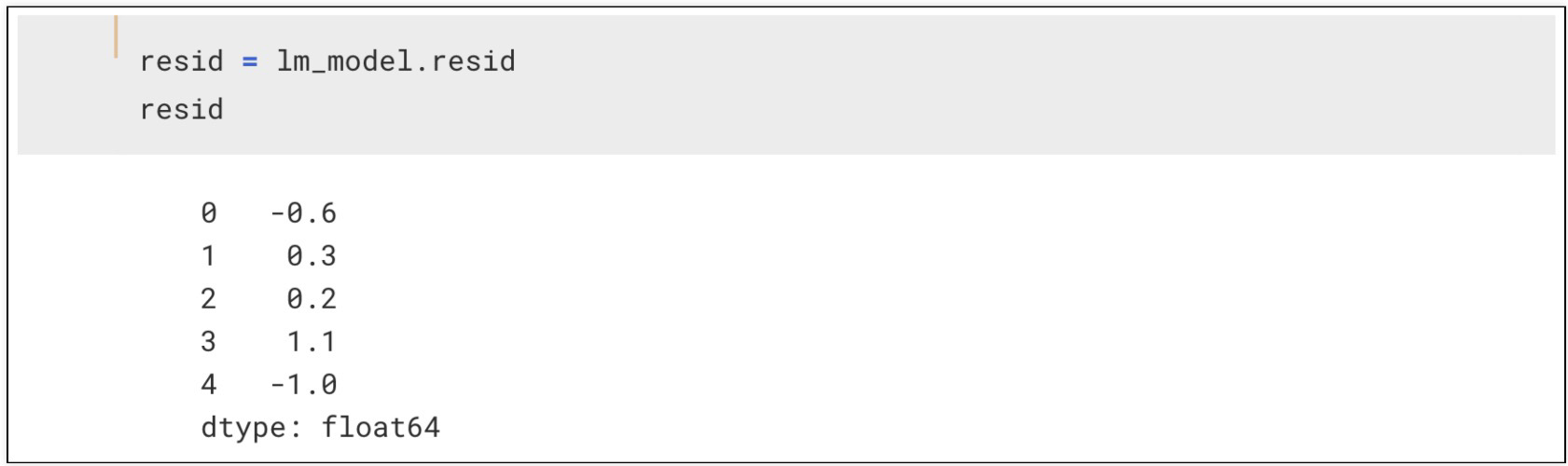
잔차의 분포도 확인
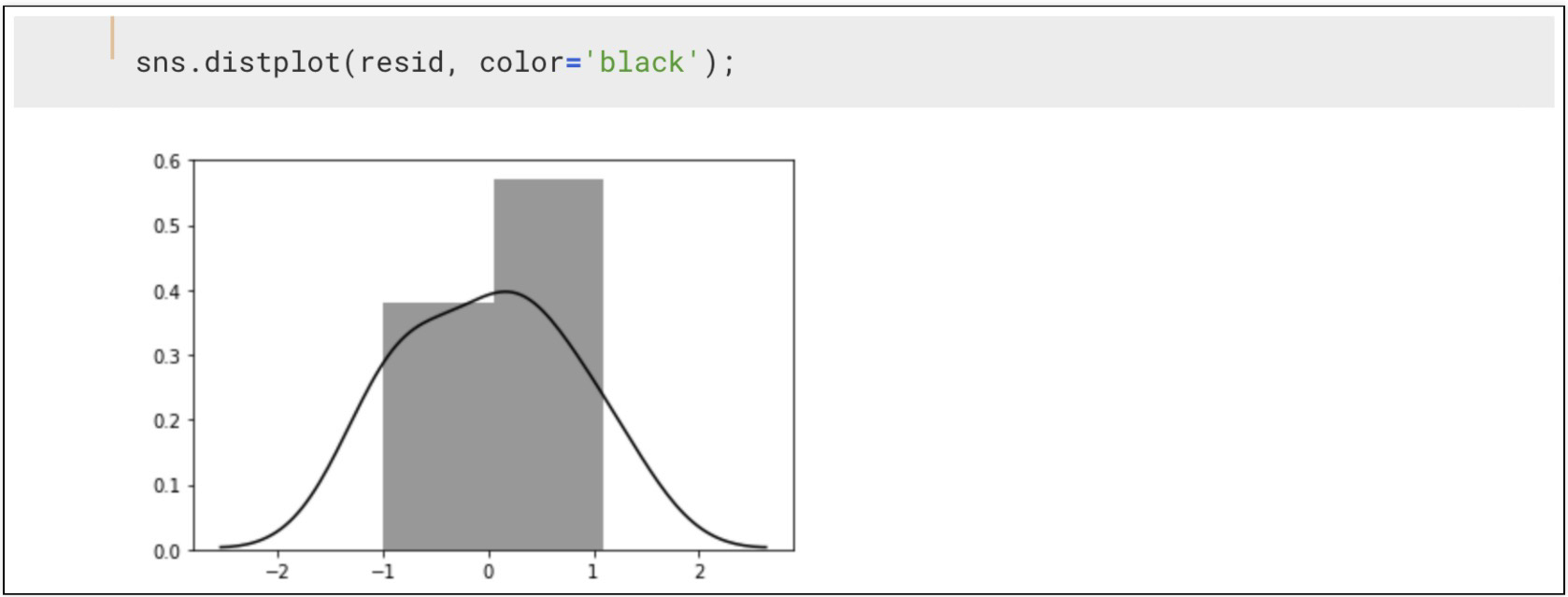
- 지도학습 - 분류 classification
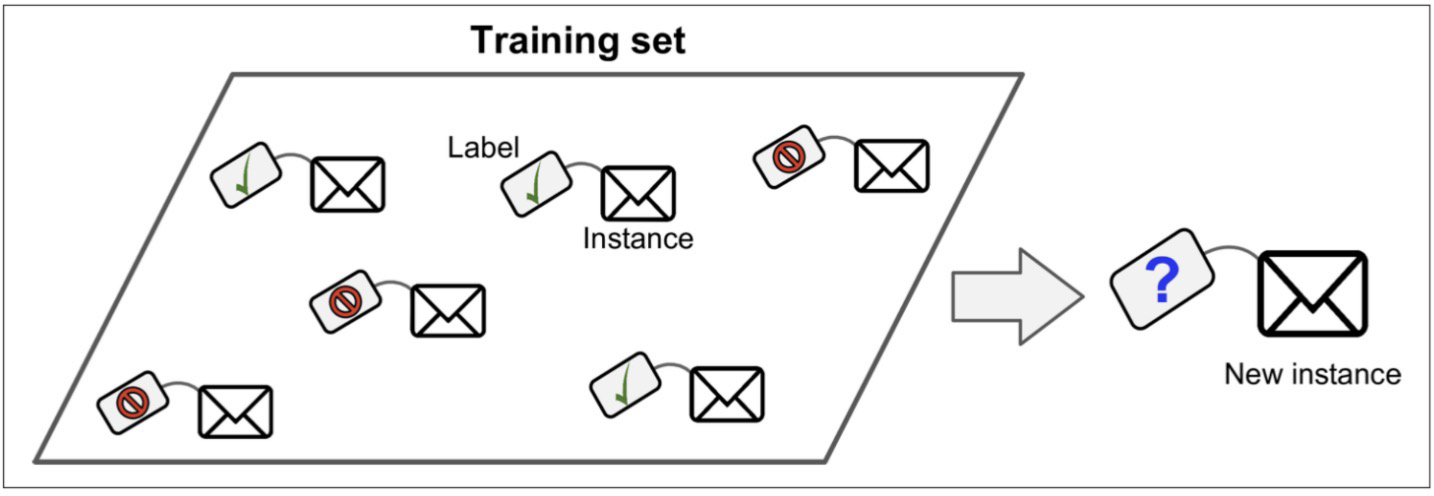
결정계수 R-Squared
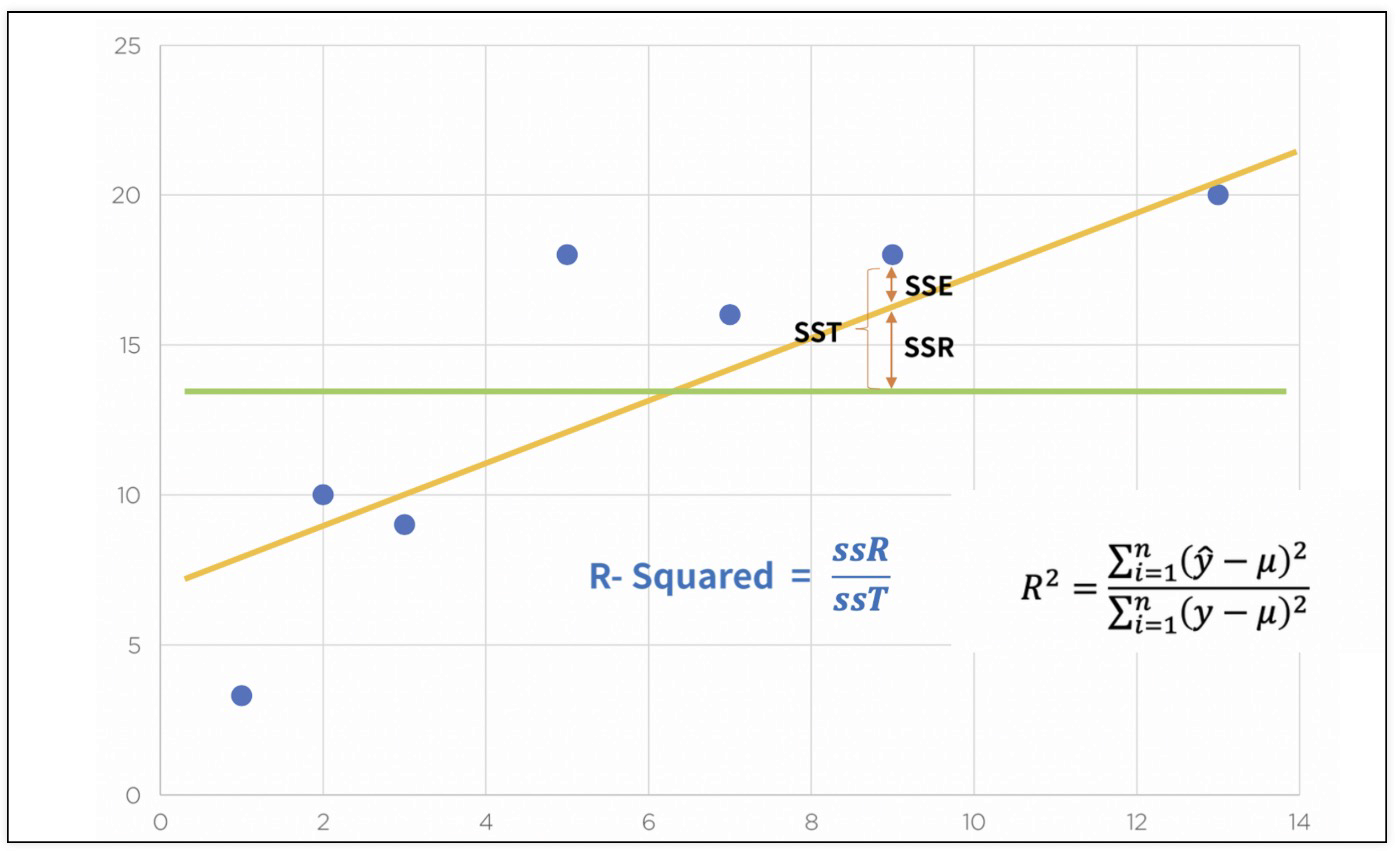

예측된 값(y-hat)을 바탕으로 결정계수 계산하며,
예측된 값이 실제 값과 일치하면 결정계수는 1이됨
결정 계수가 높을 수록 좋은 모델
비지도학습
비지도 학습은 레이블이 없다.
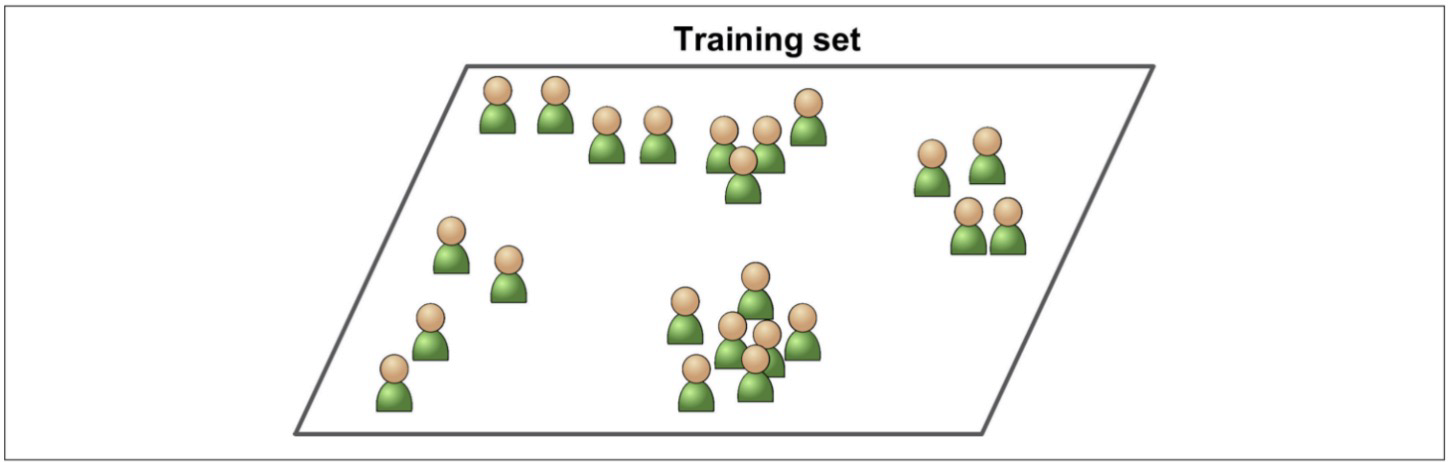
비지도학습 - 군집
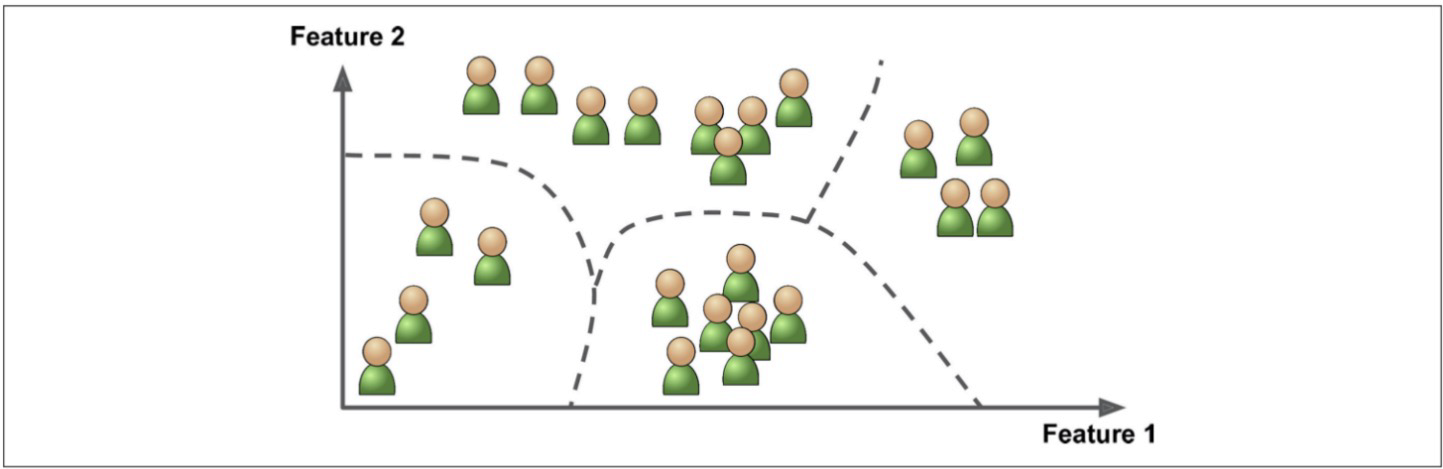
비지도학습(Unsupervised Learning)에서의 군집(Clustering)은 데이터를 유사한 특성을 가진 그룹으로 나누는 기법
군집 분석은 데이터 내에서 내재된 패턴이나 구조를 발견하고 이해하는 데 사용
주어진 데이터를 사전에 정의된 레이블이나 카테고리 없이 비슷한 특성을 가진 클러스터로 그룹화하는 작업
군집 특징
1. 비지도 학습:
모델은 데이터의 패턴을 찾아내기 위해 입력 데이터만을 사용합니다.
2. 유사성 기반 그룹화:
군집은 데이터 간의 유사성을 기반으로 그룹화
유사한 데이터들은 같은 클러스터에 속하게 됩니다.
3. 중심 기반 또는 계층적 군집:
군집 기법은 다양한 형태로 구현
예) 데이터의 중심을 기준으로 클러스터를 형성 / 계층적인 구조로 데이터를 그룹화
4. 응용 분야:
예) 고객 세분화, 이미지 분할, 유전체 분석, 소셜 미디어 분석 등에서 데이터의 유사성을 기반으로 유용한 정보를 추출
5. 평가:
군집 분석의 성능 평가는 상대적으로 주관적
따라서 내부 클러스터 유사성과 외부 클러스터 간의 분리도 등을 평가 기준으로 사용
군집 알고리즘 예시
1. K-평균 군집화:
데이터를 k개의 클러스터로 분할하며, 각 클러스터의 중심을 찾아가며 클러스터를 형성
2. 계층적 군집화:
데이터를 계층적인 트리 구조로 분할하며, 클러스터를 점차 묶어나가는 방식
3. DBSCAN(Density-Based Spatial Clustering of Applications with Noise):
밀도 기반의 군집화 방법으로, 데이터의 밀집 지역을 클러스터로 인식하고 잡음 데이터를 구분
4. GMM(Gaussian Mixture Model):
가우시안 분포를 사용하여 데이터를 여러 개의 클러스터로 나누는 방법
군집 분석은 데이터의 패턴을 발견하고 이해하는 데 중요한 도구로 활용되며, 데이터 마이닝, 패턴 인식, 고객 세분화 등 다양한 분야에서 응용됩니다.
비지도학습 - 차원 축소
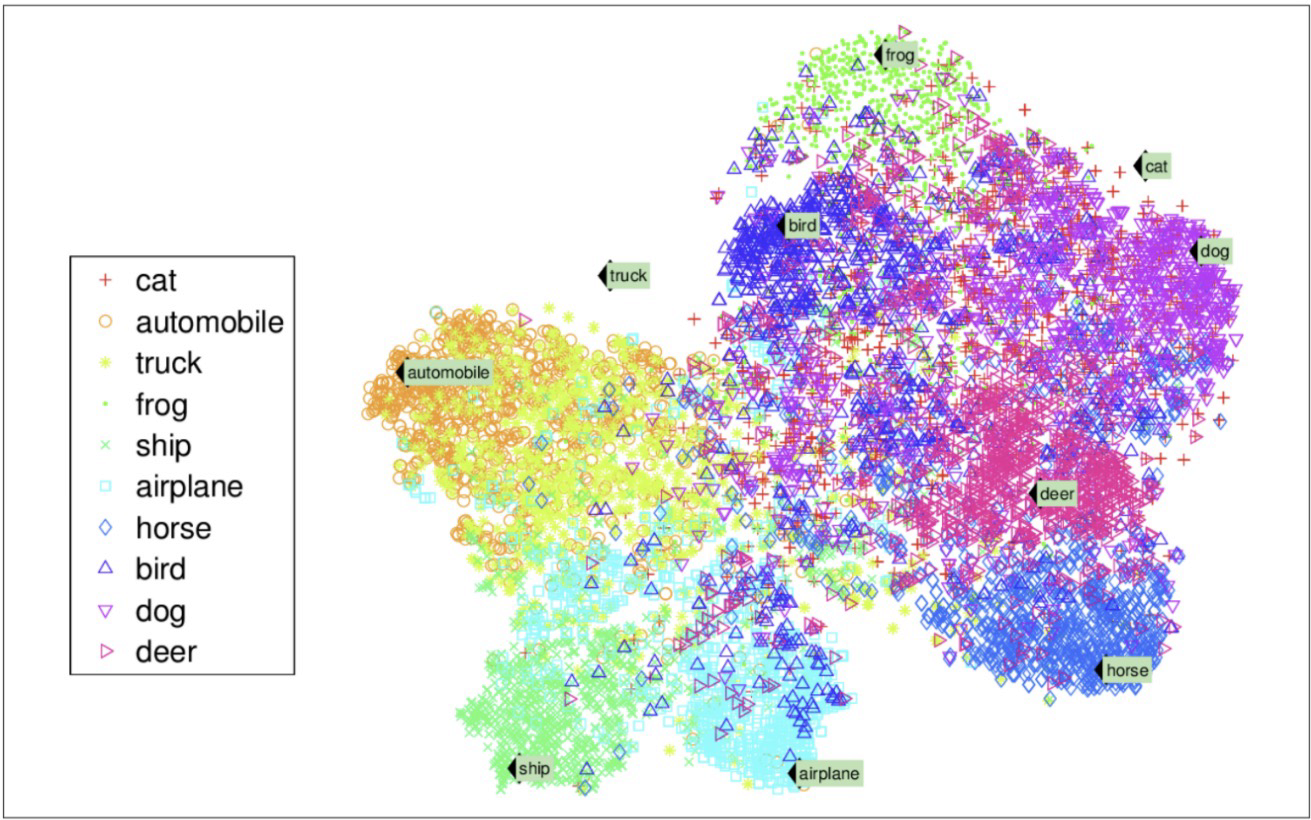
차원 축소(Dimensionality Reduction)는 데이터의 특성을 보존하면서 데이터의 차원을 줄임
고차원 데이터는 분석과 시각화에 어려움을 줄 수 있고, 모델링에 불필요한 노이즈나 과적합을 야기할 수 있습니다. 따라서 차원 축소는 데이터를 더 낮은 차원으로 투영하거나 변환하여 데이터의 복잡성을 줄이는데 사용됩니다.
차원 축소의 목표는 다음과 같습니다:
-
데이터의 시각화:
고차원 데이터는 시각화하기 어려울 수 있습니다. 차원 축소를 통해 데이터를 2D 또는 3D로 표현하여 데이터 간의 관계와 패턴을 이해하기 쉽게 만들 수 있습니다. -
데이터 압축:
차원 축소를 통해 데이터의 차원을 줄임으로써 데이터를 효율적으로 저장하고 처리할 수 있습니다. -
노이즈 제거:
고차원 데이터에는 노이즈나 불필요한 정보가 포함될 수 있습니다. 차원 축소를 통해 이러한 노이즈를 제거하거나 줄일 수 있습니다. -
모델 성능 개선:
차원 축소를 통해 모델의 학습 시간을 줄이거나 모델의 성능을 향상시킬 수 있습니다. 더 적은 차원에서 작업하는 것이 일반적으로 더 효율적입니다.
주요한 차원 축소 기법으로는 다음과 같은 것들이 있습니다:
-
주성분 분석(PCA, Principal Component Analysis): 데이터의 분산을 최대한 보존하면서 주요한 특성을 찾아 데이터를 새로운 축으로 변환하는 방법입니다.
-
t-SNE(t-Distributed Stochastic Neighbor Embedding): 고차원 데이터의 유사도를 보존하면서 저차원으로 투영하여 시각화하는 방법입니다.
-
LLE(Locally Linear Embedding): 이웃 데이터 포인트 간의 선형 관계를 유지하면서 저차원으로 투영하는 방법입니다.
-
Autoencoder: 신경망 기반의 모델로, 입력 데이터를 저차원 표현으로 압축하고 다시 복원하여 원본 데이터와 유사한 표현을 찾는 방법입니다.
차원 축소는 데이터의 특성과 목표에 따라 적절한 기법을 선택하여 사용합니다. 이를 통해 데이터의 차원을 줄이면서 중요한 정보를 보존하거나 시각화할 수 있습니다.
통계적 회귀
데이터 구조
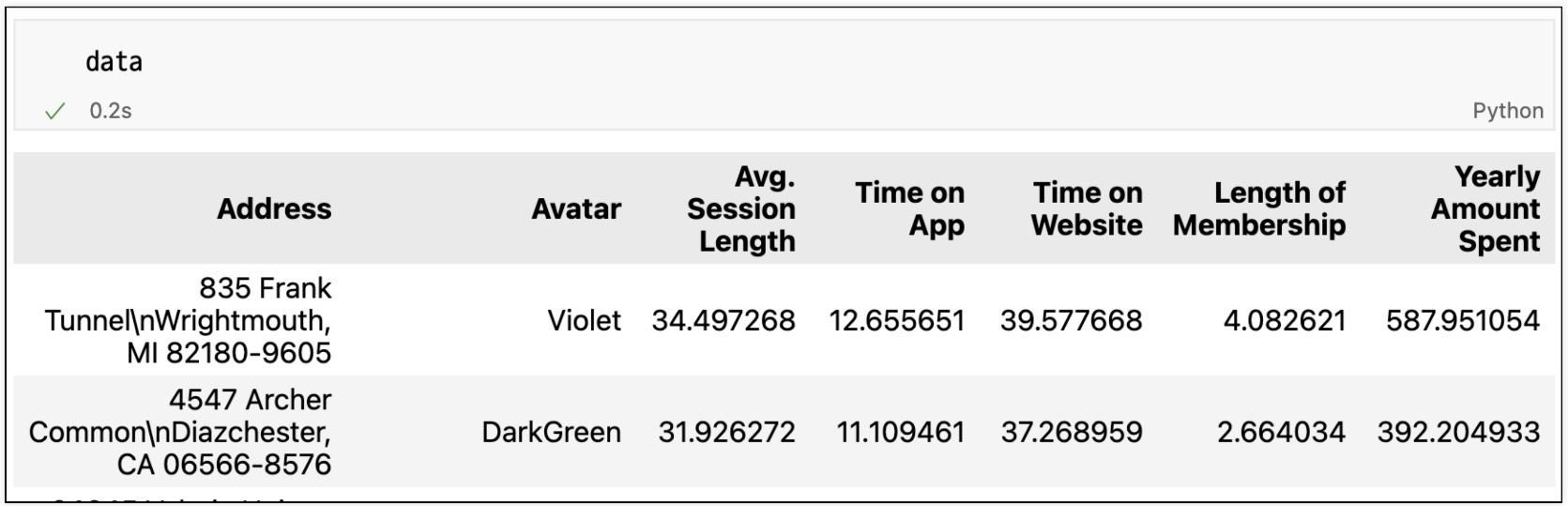
- 사용자 세션 길이는 '한번 접속 하였을 때 평균 어느정도의 기간을 사용하는지에 대한 데이터'
- time on app : 어플로 접속했을 때 유지 시간 (분)
- time on website : 웹사이트로 접속했을때 유지 시간(분)
- length of membership : 회원 자격 유지기간(연)
필요없는 컬럼 삭제
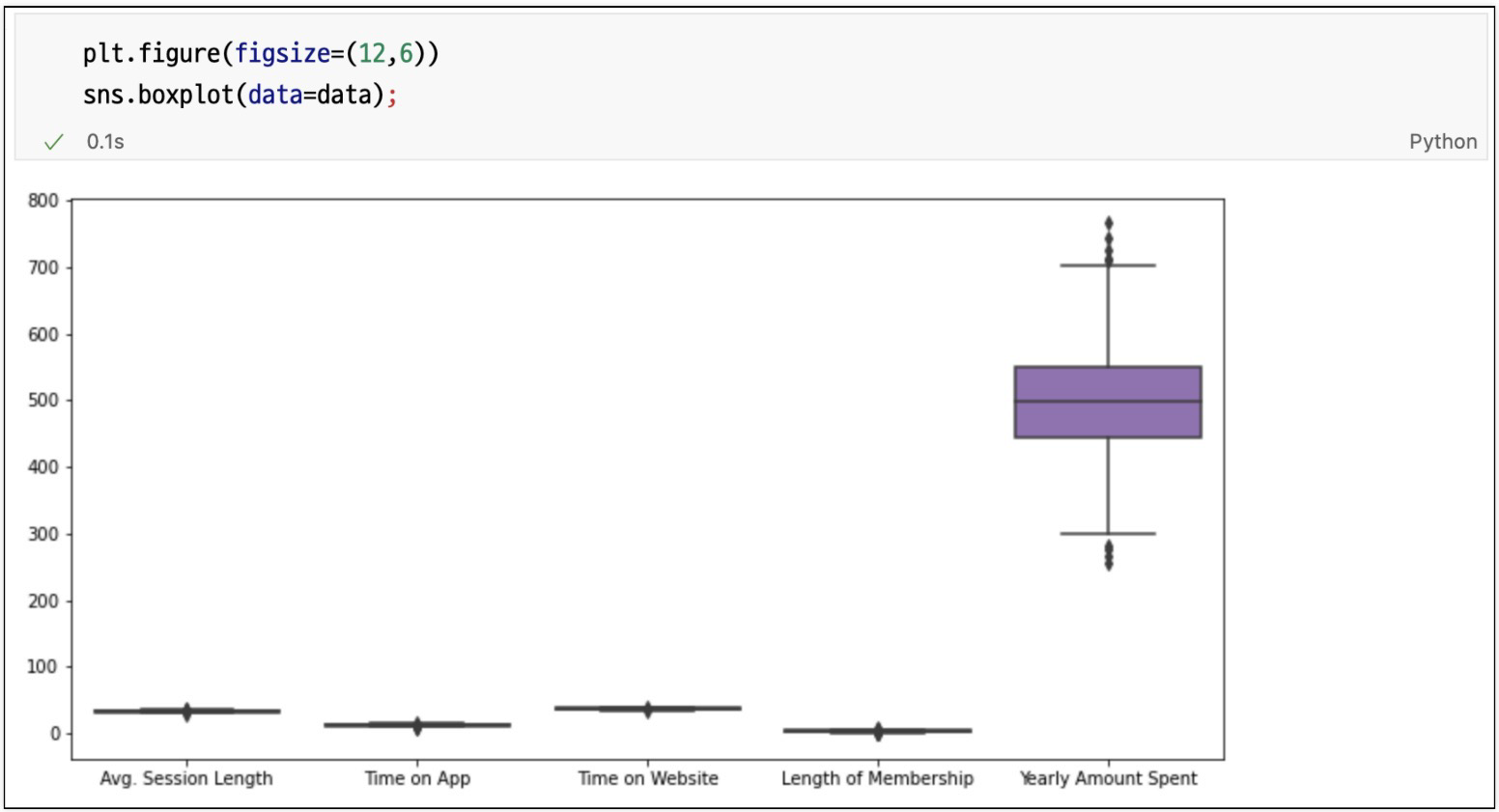
컬럼별 boxplot
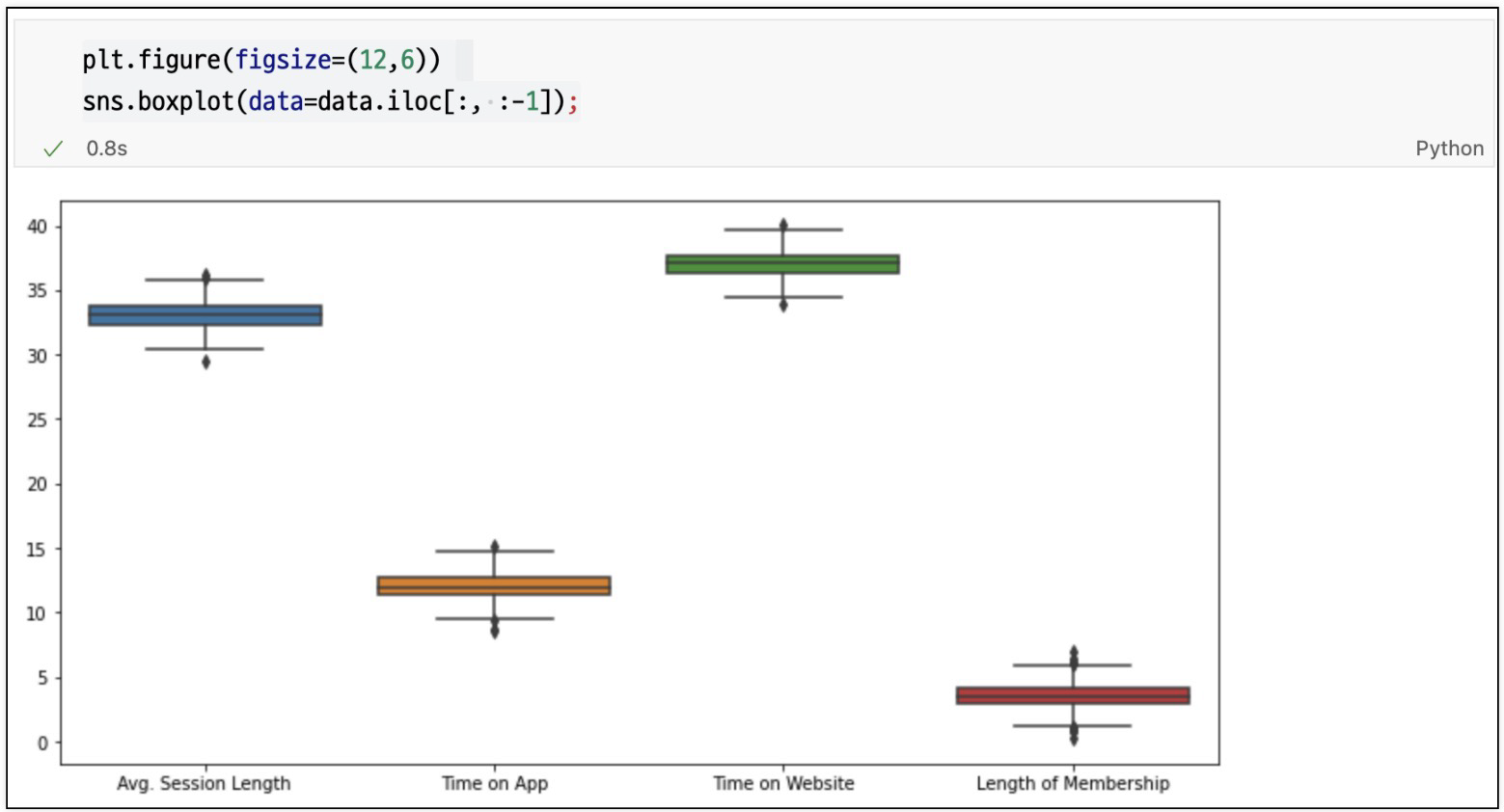
필요특성들만 다시 boxplot
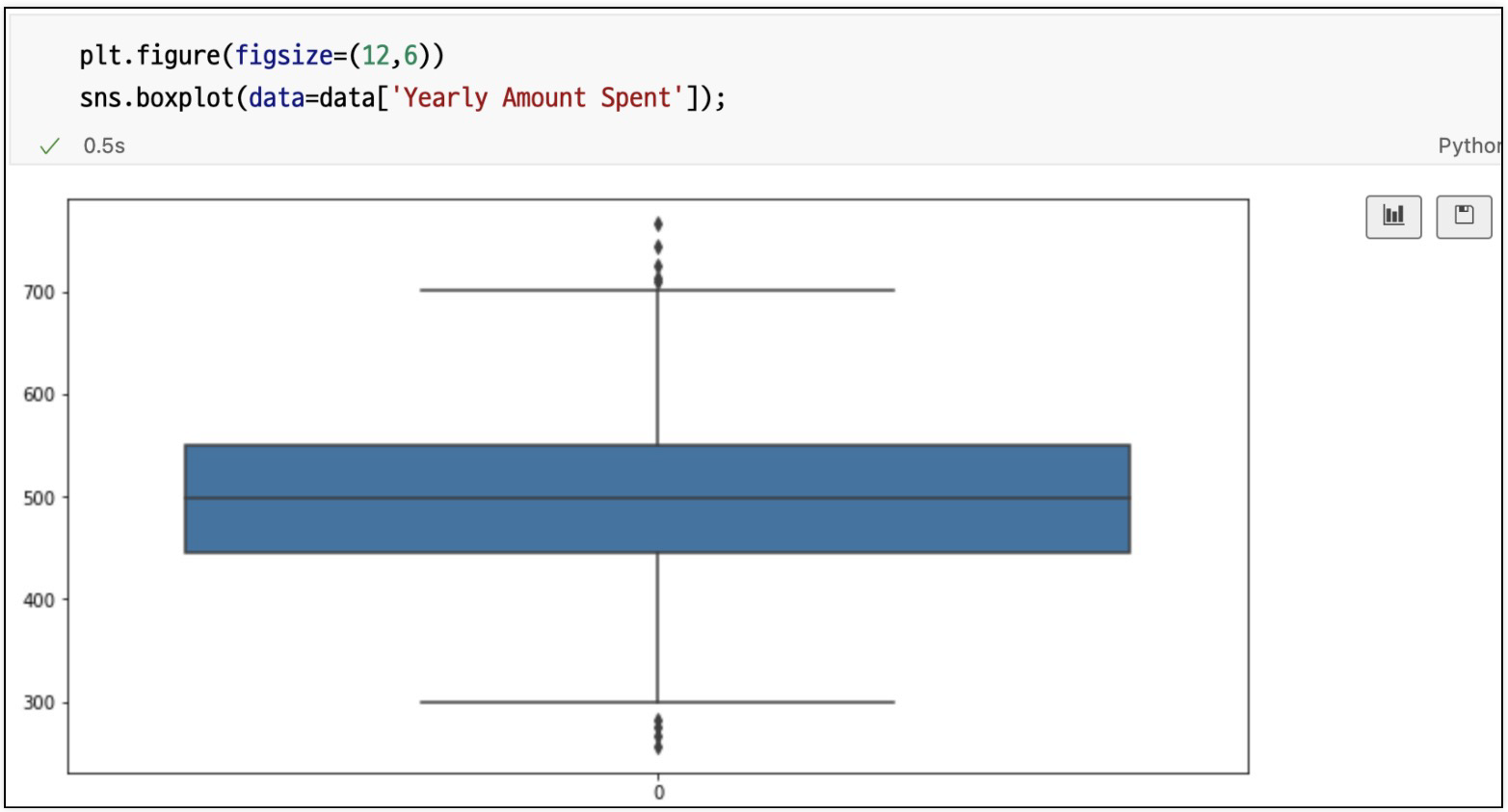
pairplot으로 경향 확인

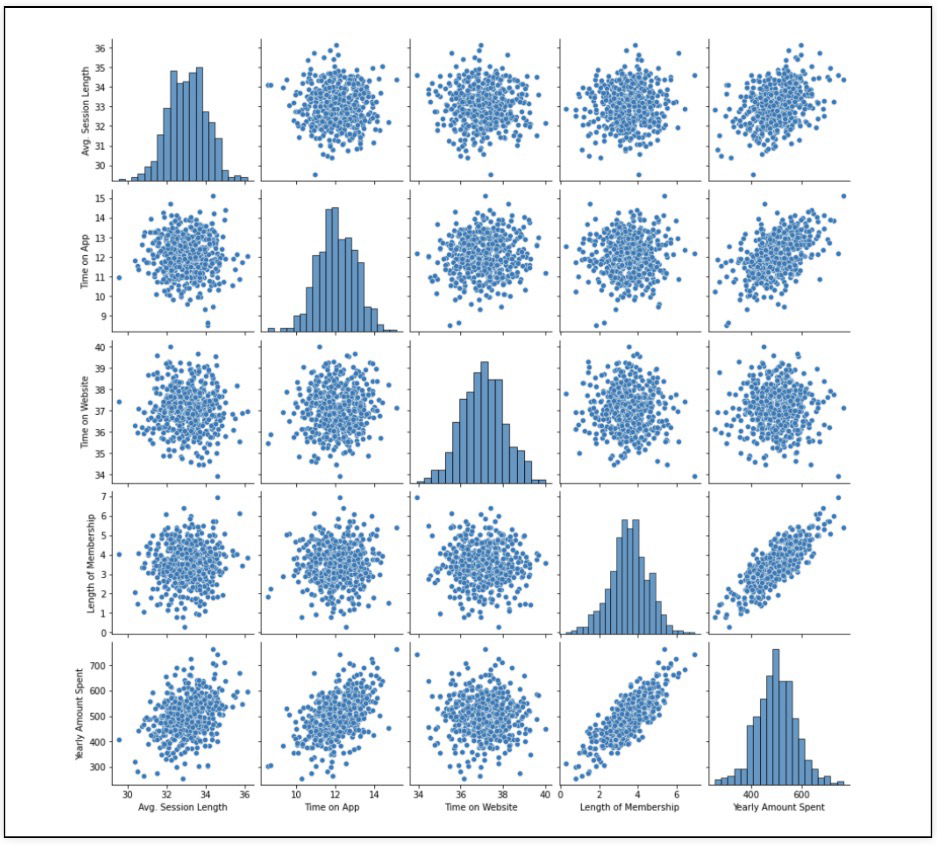
가장 큰 상관관계가 보이는 것은 멤버쉽 유지 기간
멤버쉽 유지기간에 대해 시각화(lmplot)
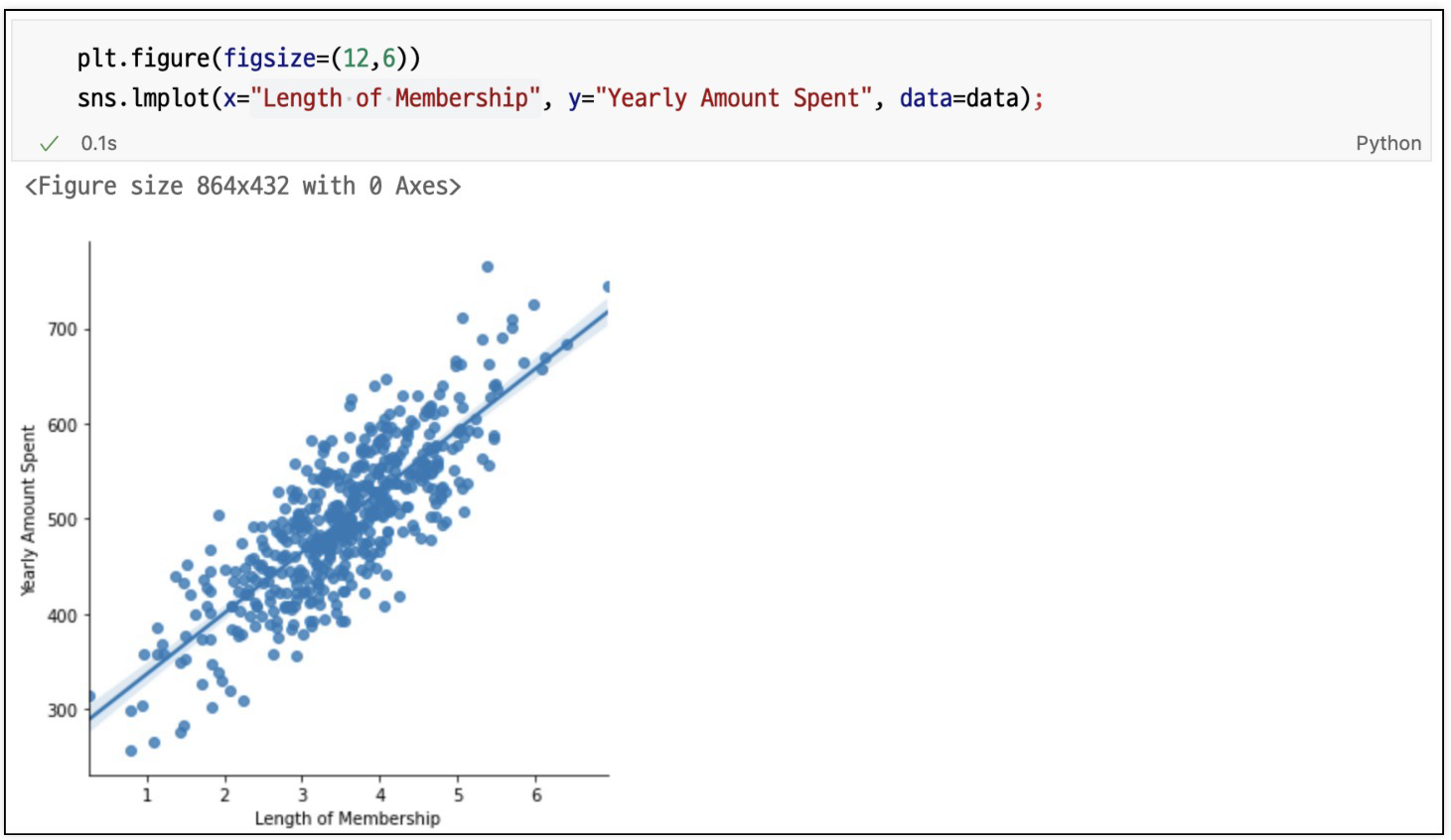
멤버쉽 유지기간만 가지고 통계적 회귀

회귀 리포트
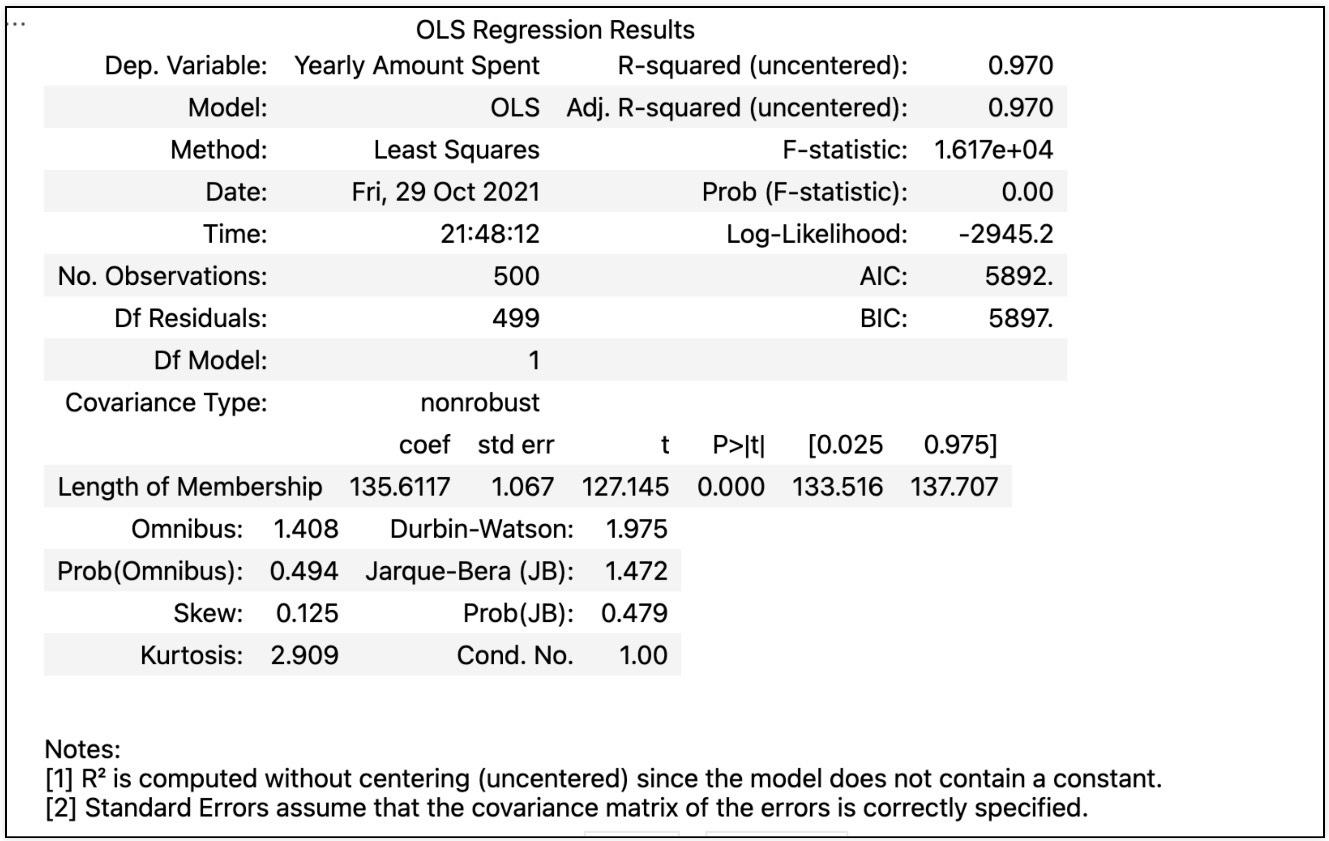
R-squared : 모형 적합도
Adj.R-squared : 독립변수가 여러개인 다중회귀분석에서 사용
Prob. F-Statistic : 회귀 모형에 대한 통계적 유의미성 검정. 이 값이 0.05이하라면 모집단에서도 의미가 있음
회귀 모델 시각화
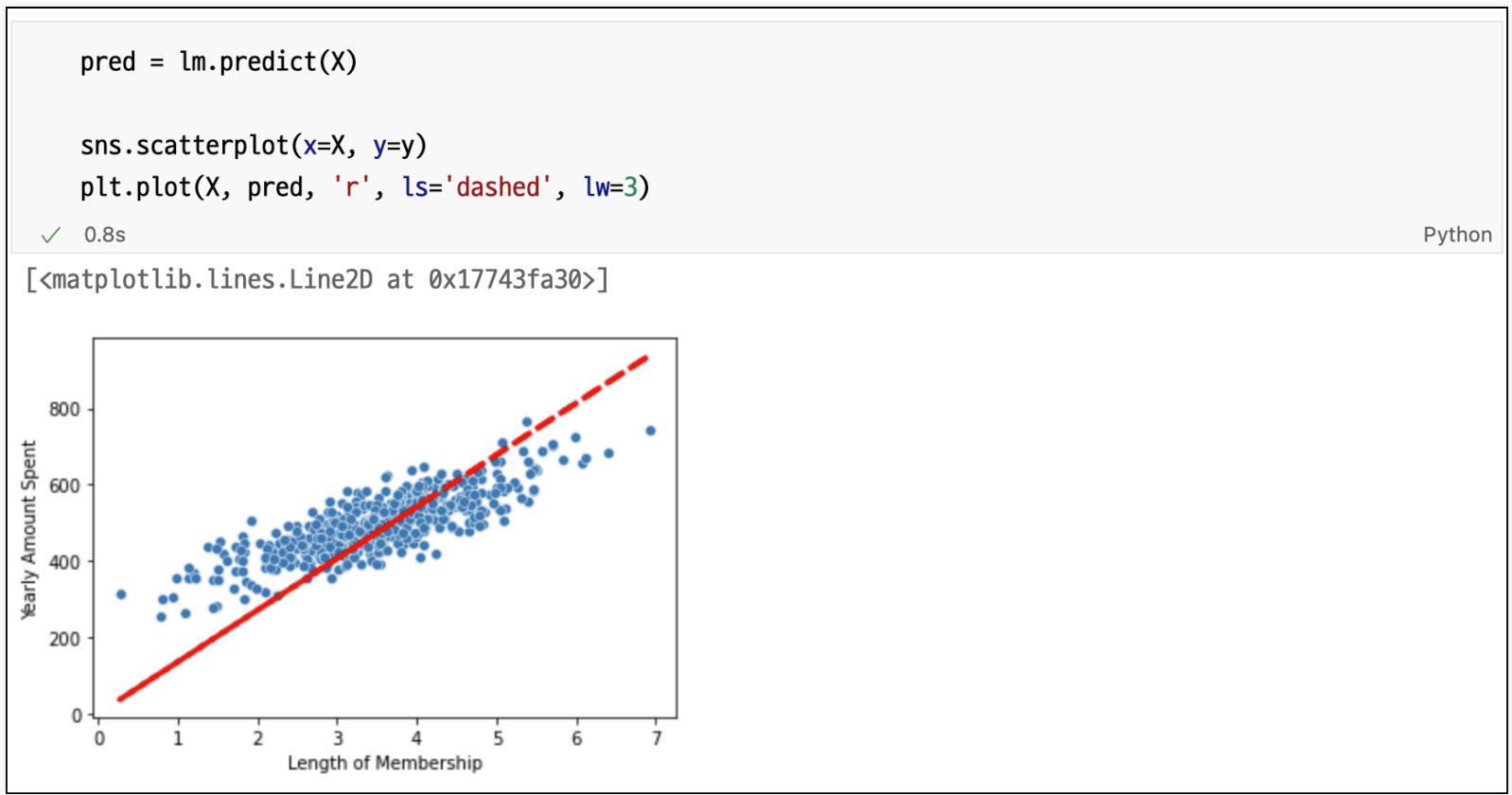
참 값 vs 예측 값
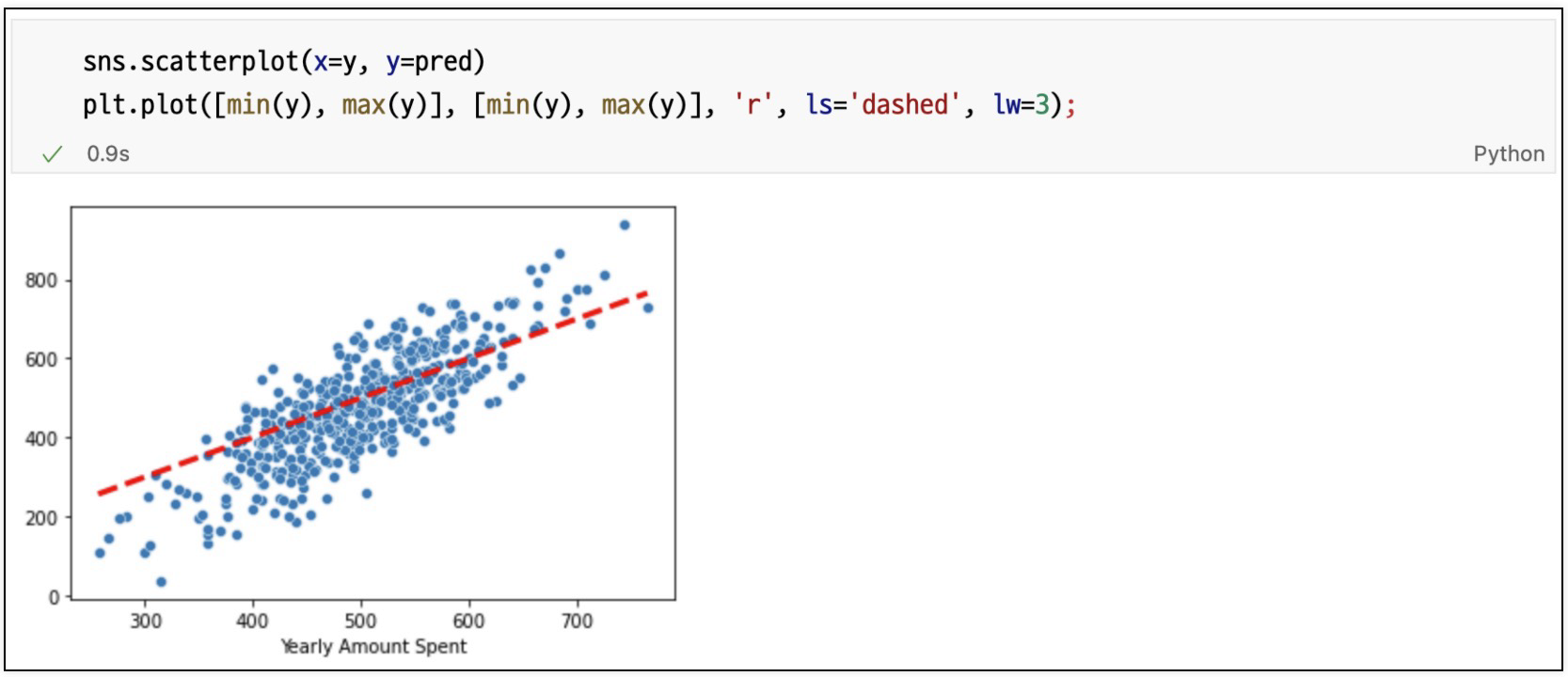
모델 fit하고 재 시각화

리포트
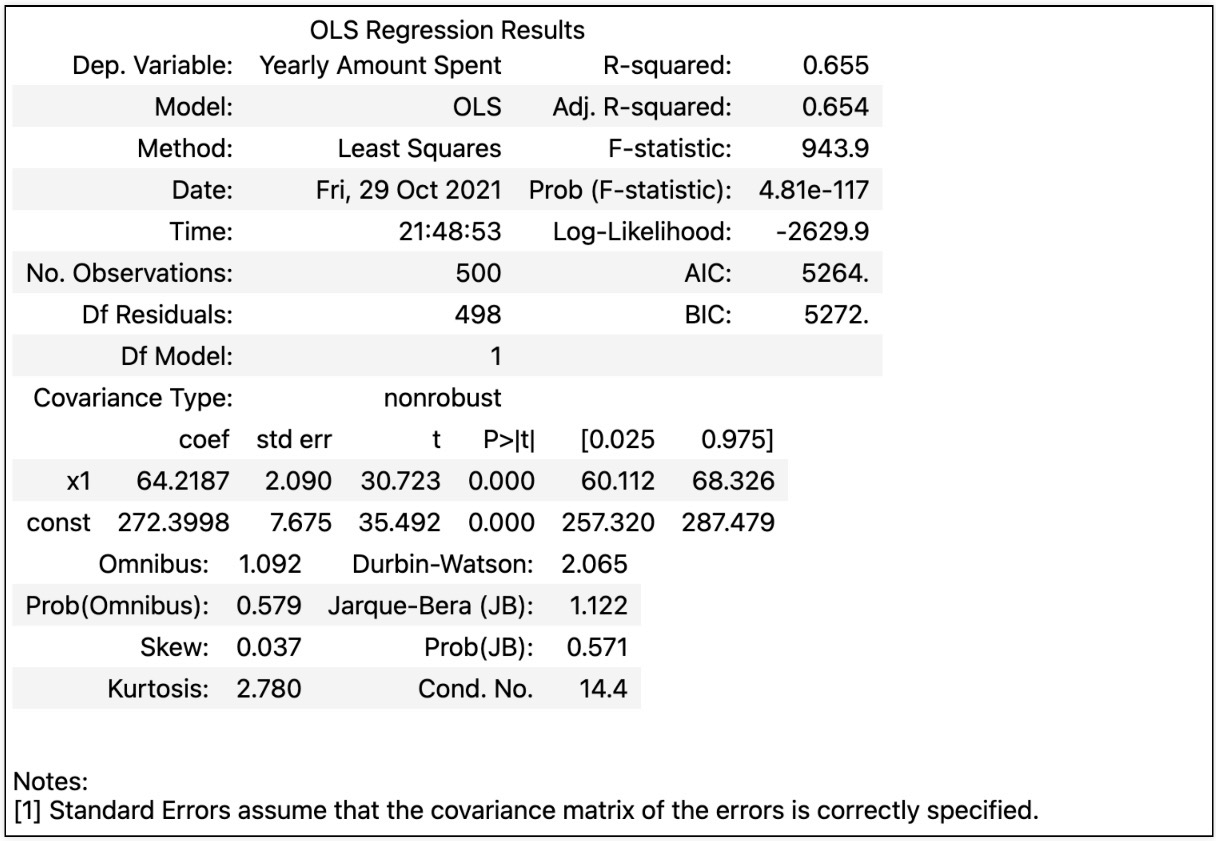
선형회귀 결과
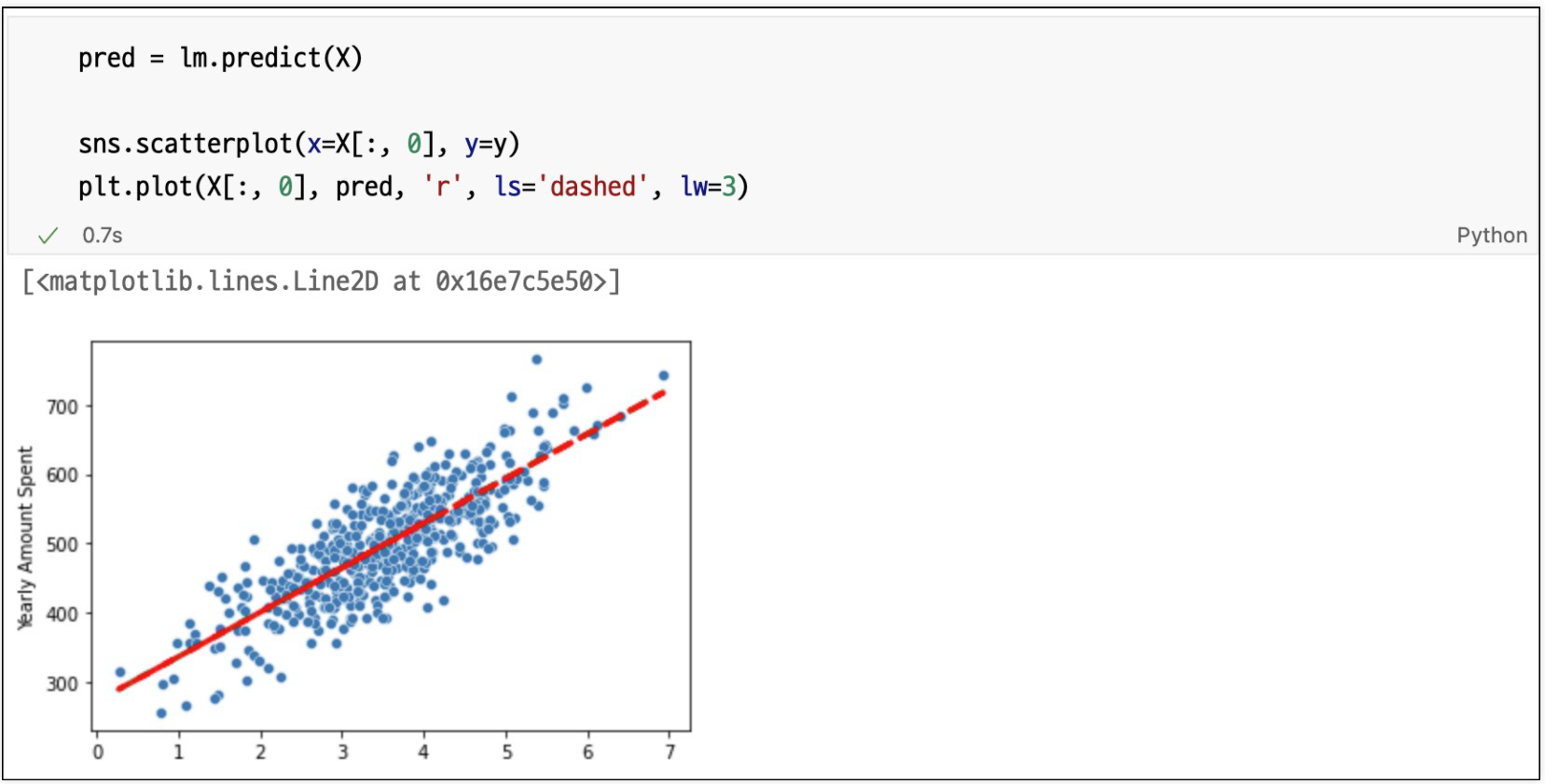
참 값 vs 예측 값
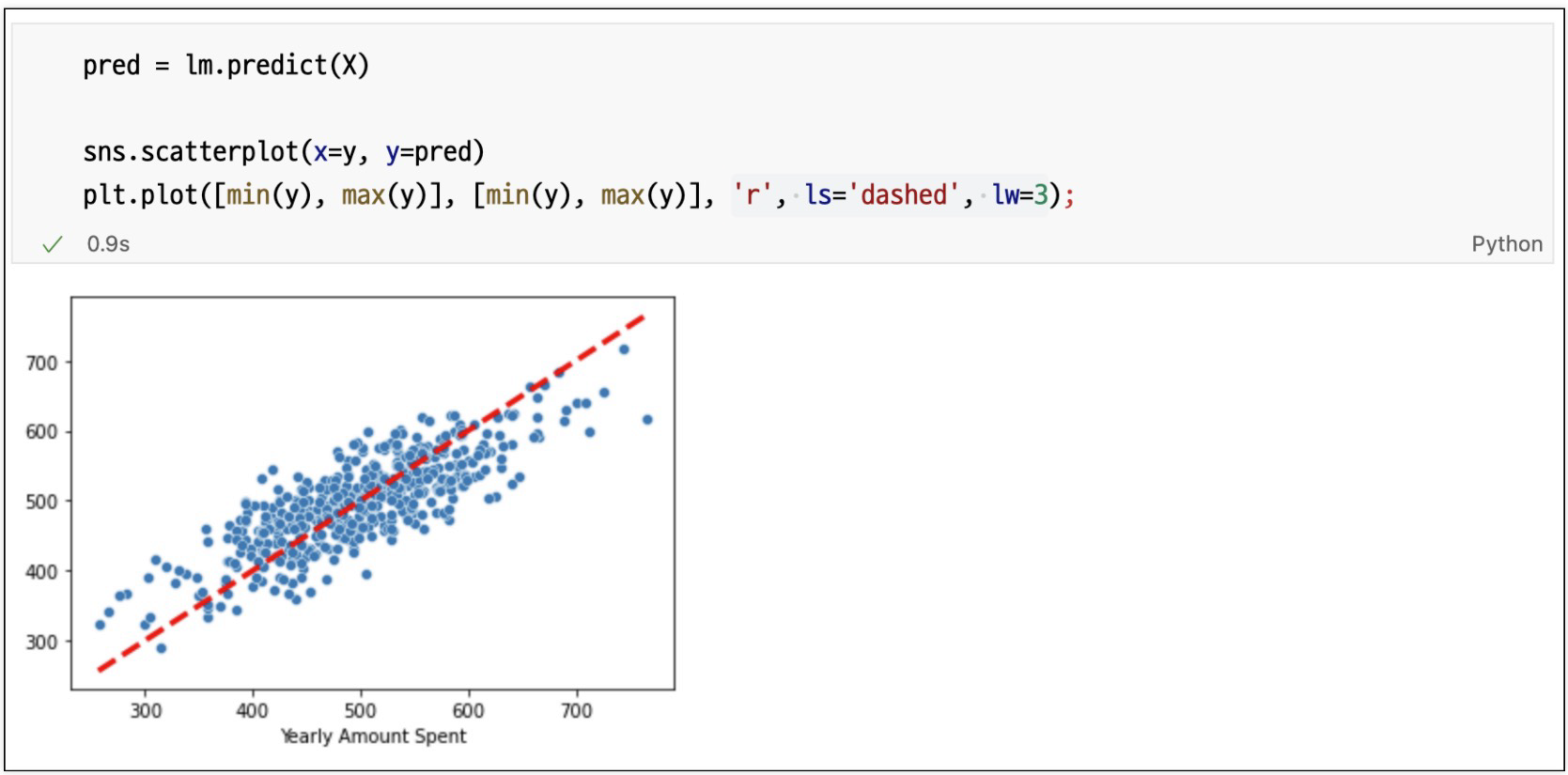
train, test로 분리후 재시각화

네개 컬럼 모두 변수로 보고 회귀

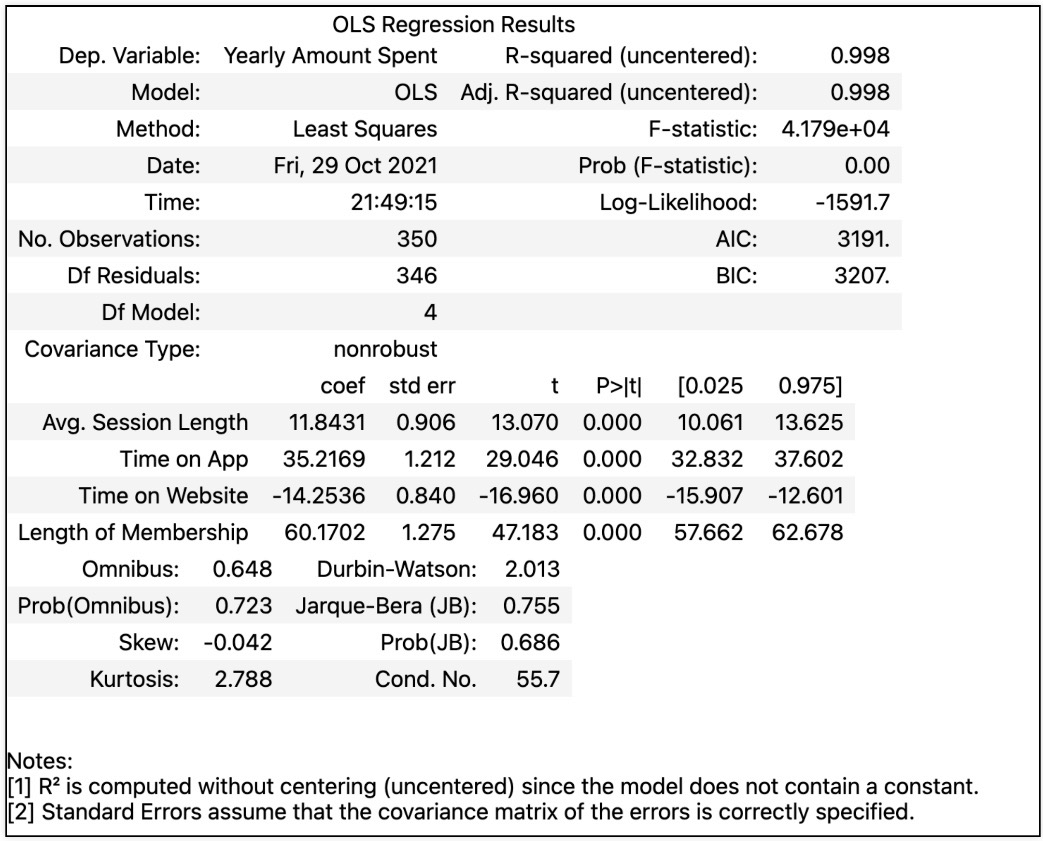
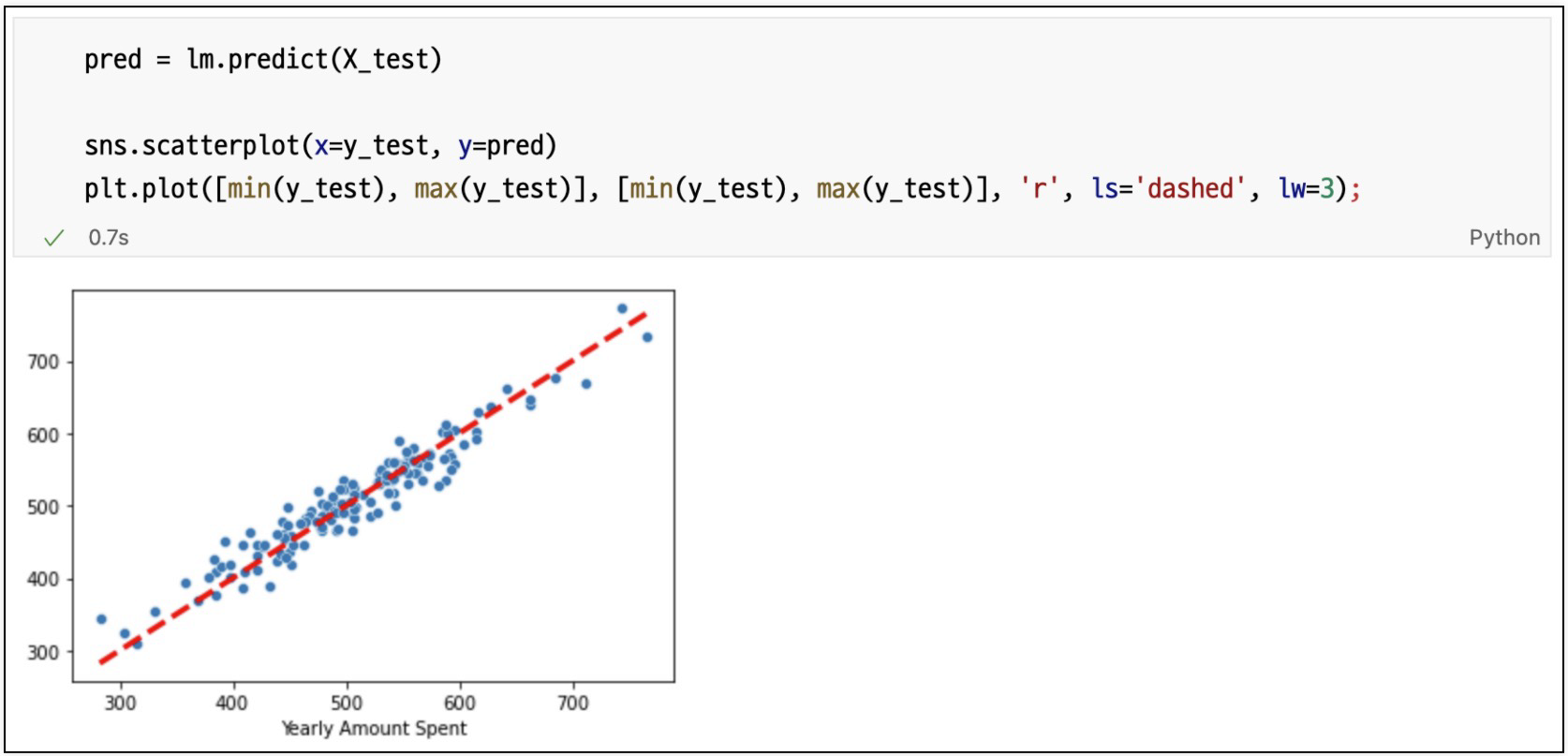
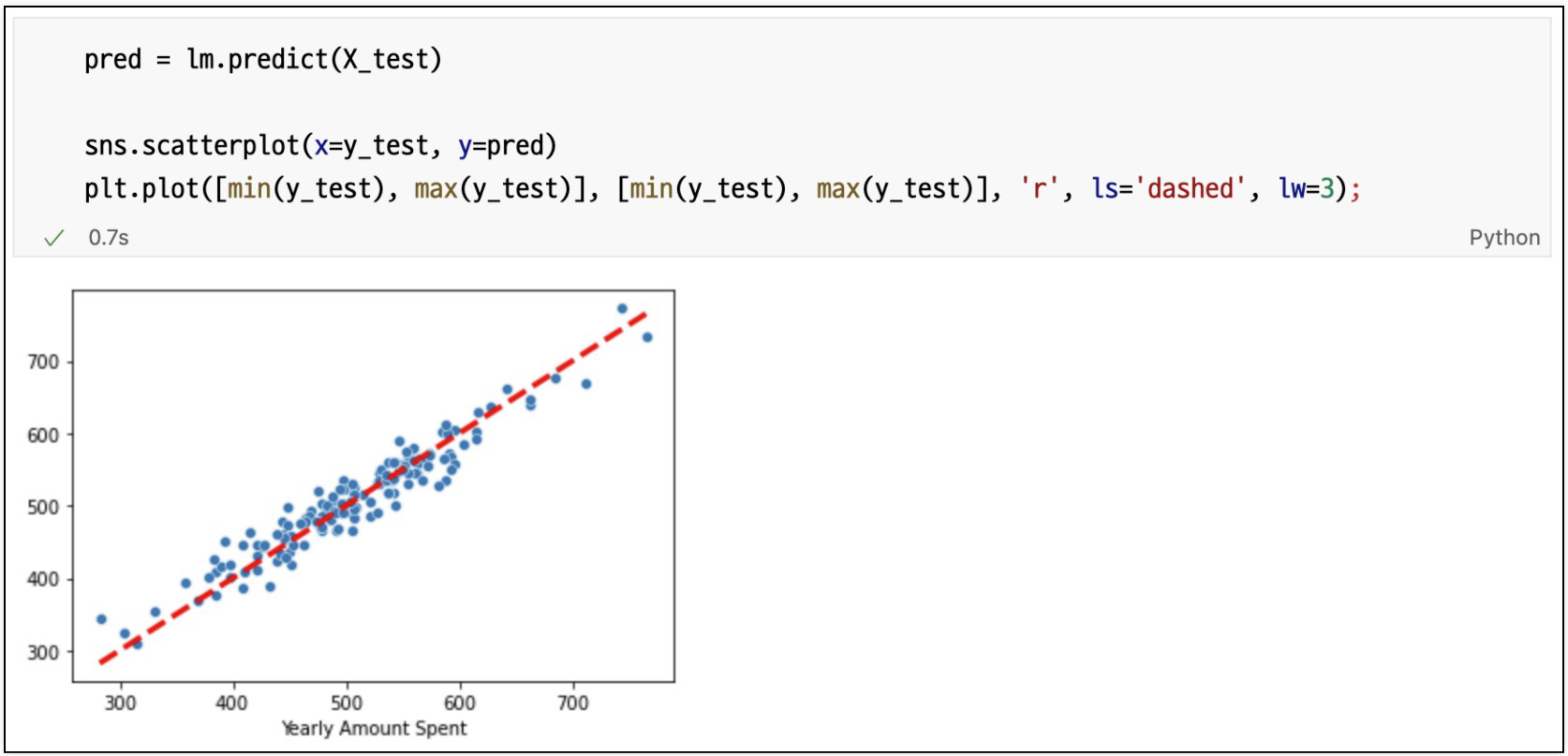
다변수 데이터에 대한 회귀
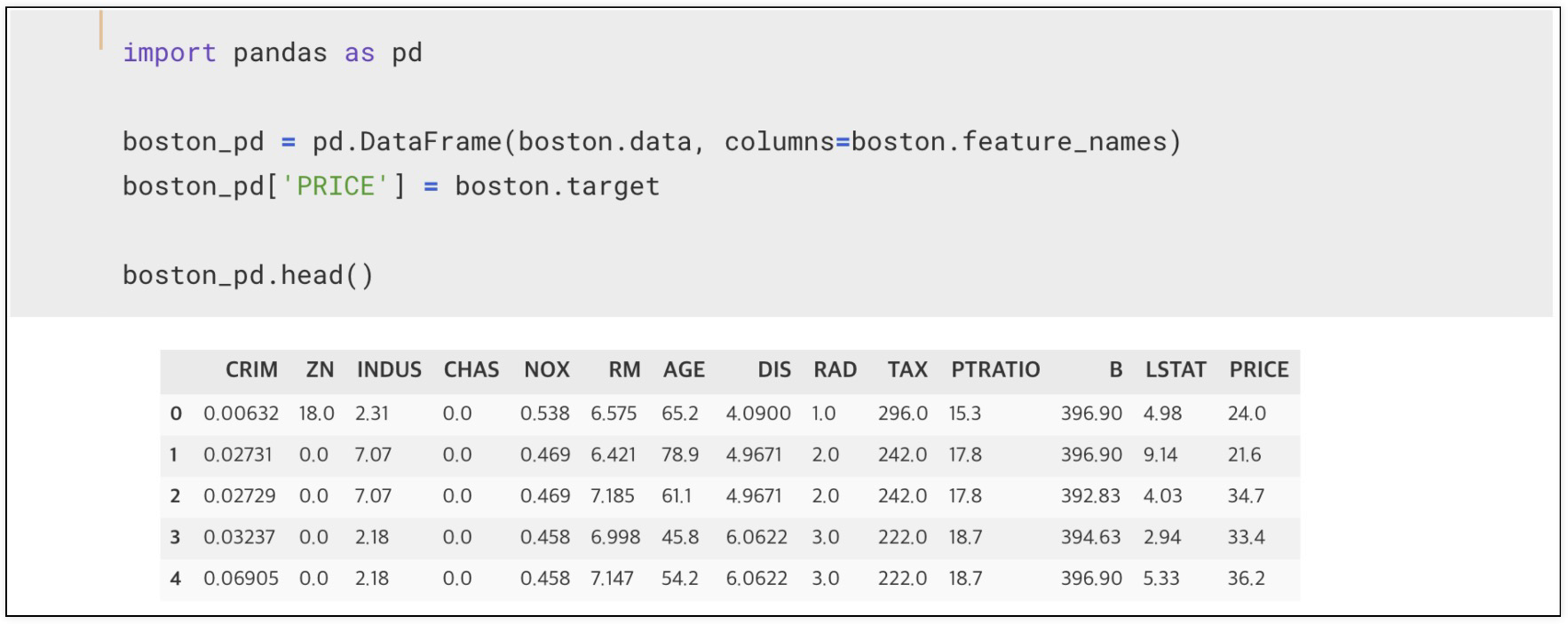
예시) 보스턴 집값
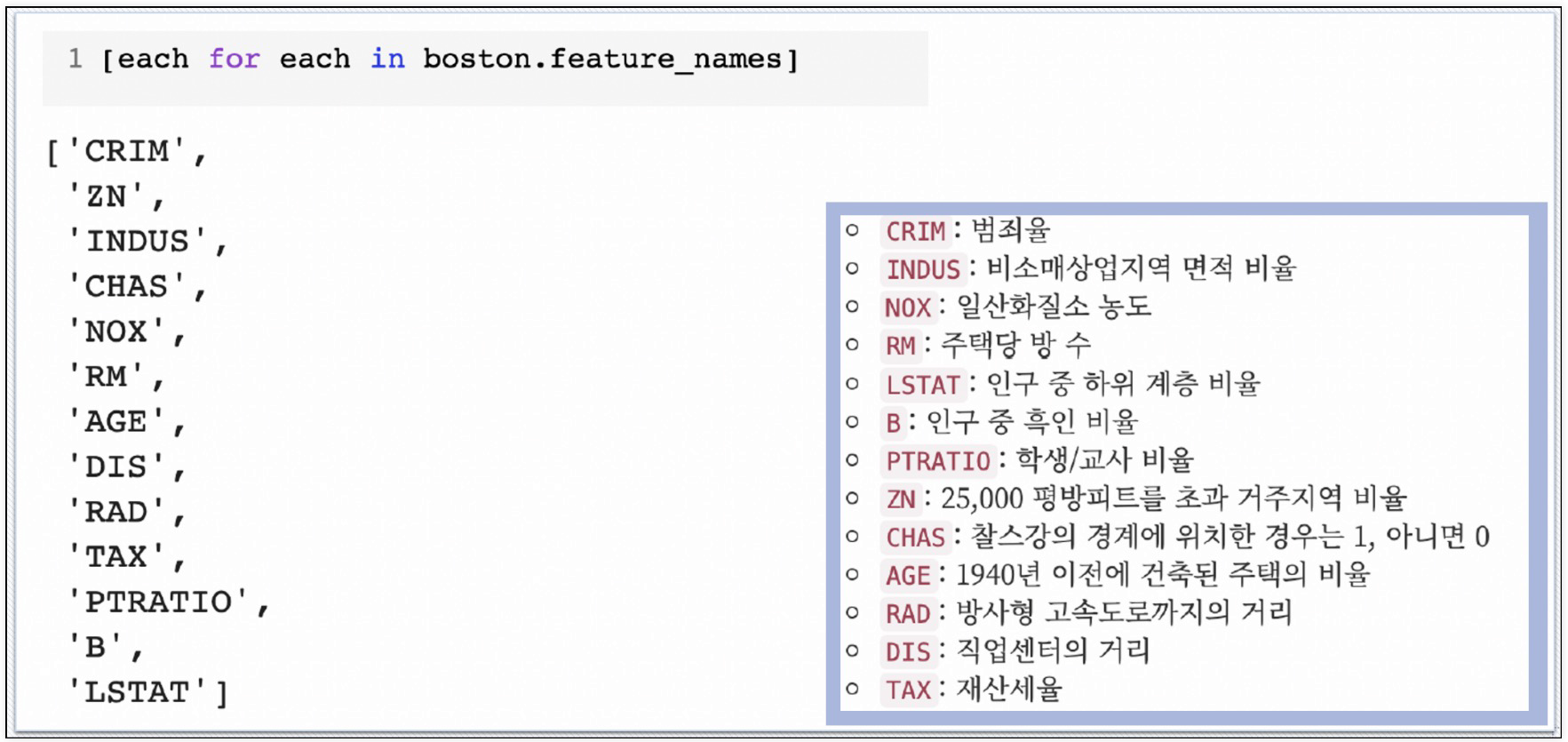
데이터 파악을 위해 정리
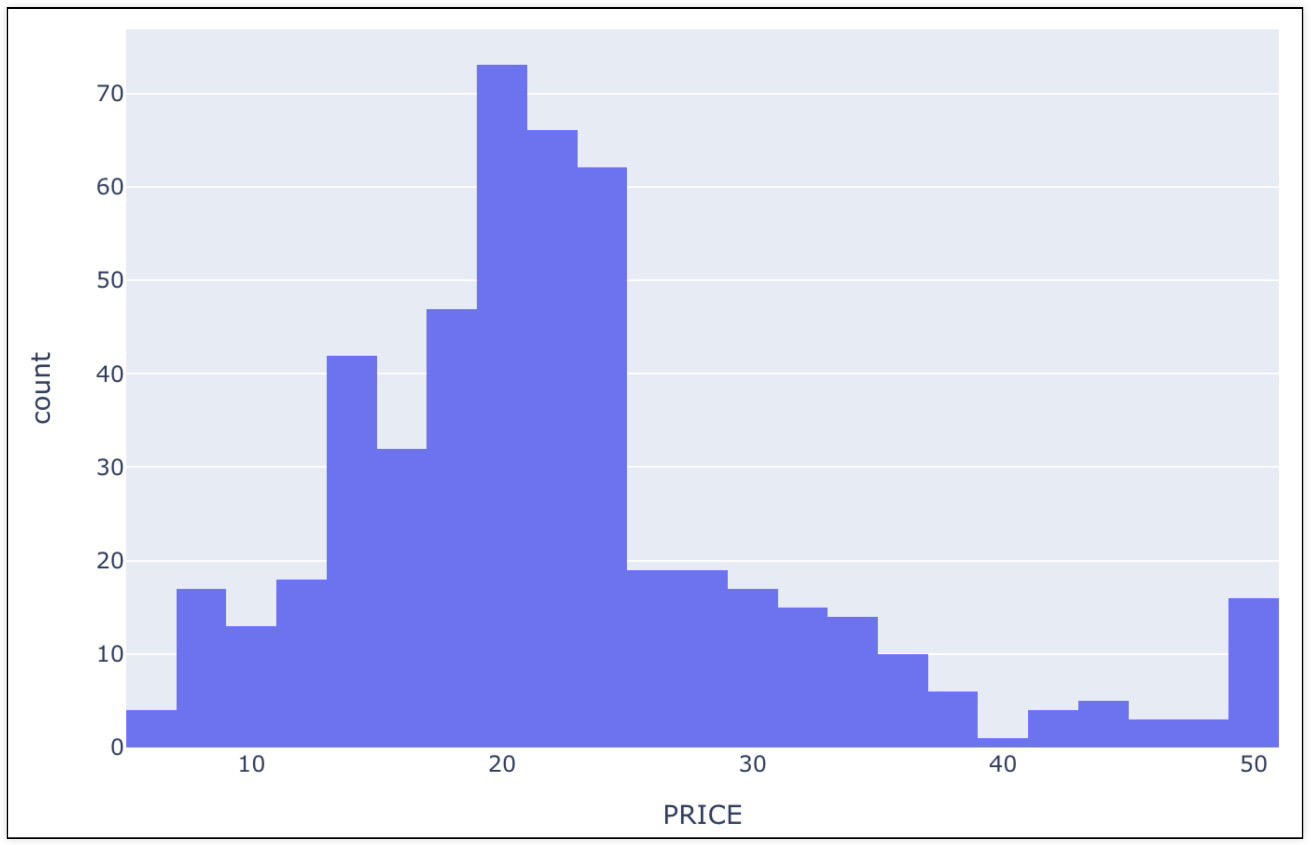
집값에 대한 히스토그램으로 분포 확인
각 특성별 상관계수 확인

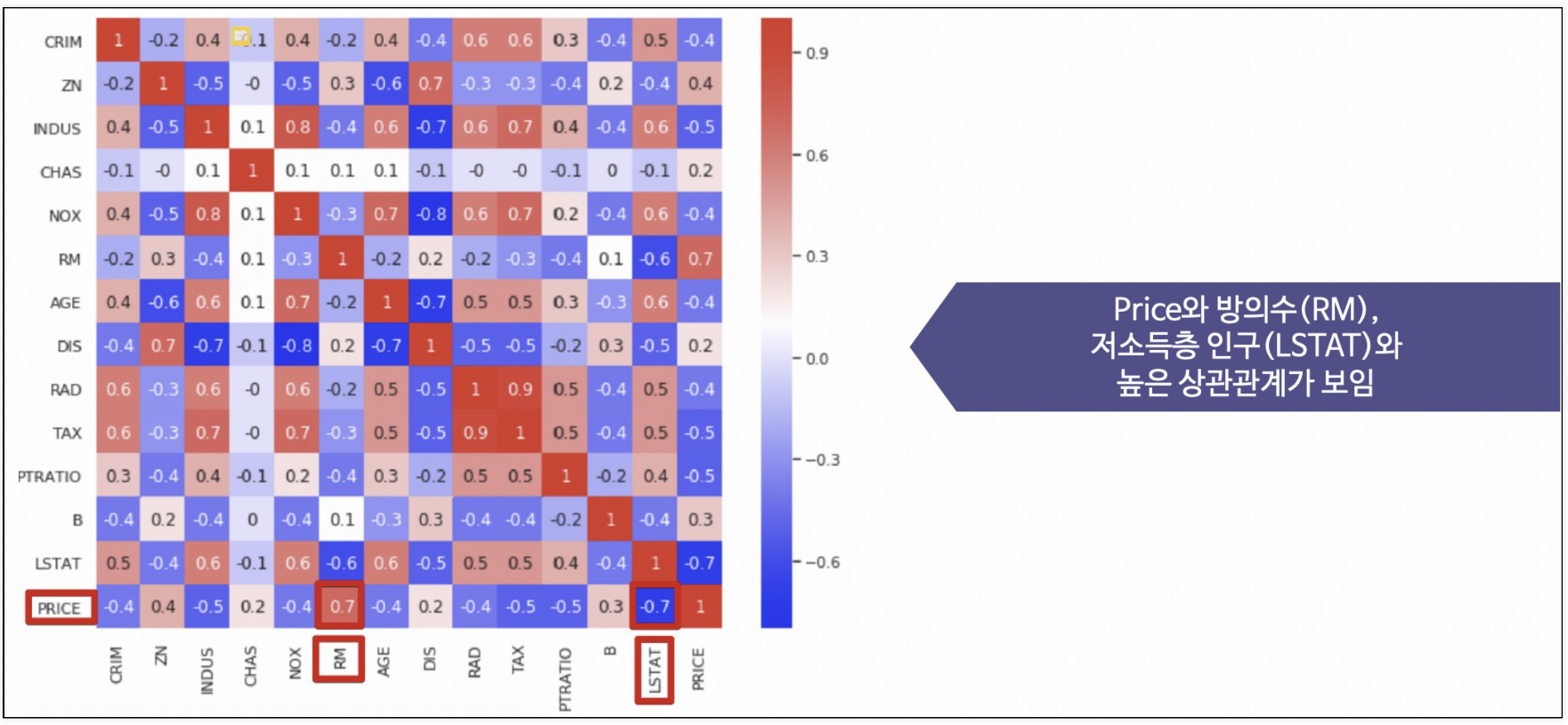
price는
room amount(방의 수), lstat(저소득층 인구)가 높은 상관관계를 보임
rm(방의 수), lstata(저소득층 인구)와 price(집값)의 관계에 대해 확인

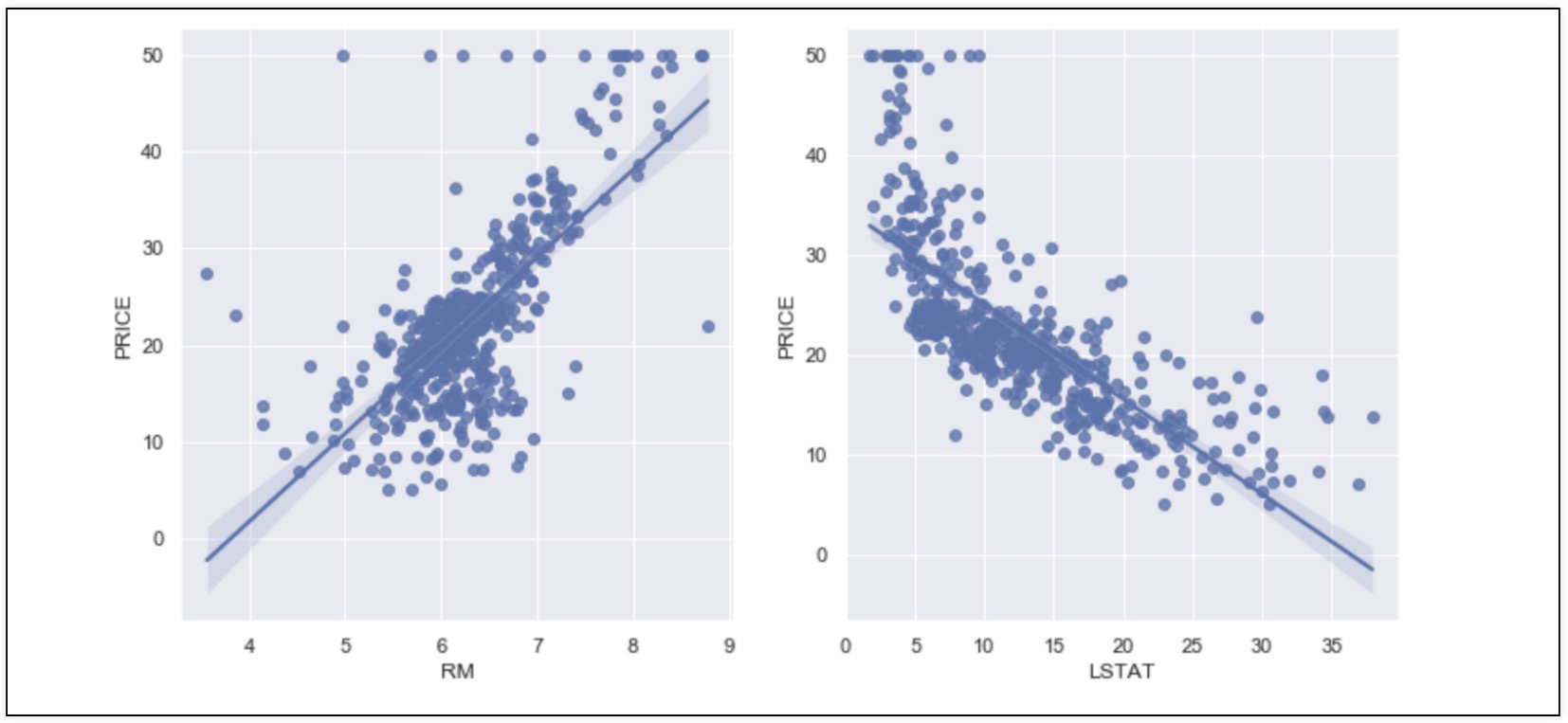
저소득층 인구가 낮을수록, 방의 개수가 높을수록 집 값이 높아진다.
이 가설은 문제가 없는게 맞을까?
훈련,테스트용으로 데이터 나누고

linerregression

RMSE로 모델평가하고
RMSE는 "Root Mean Squared Error"의 약어로, 회귀 분석에서 모델의 예측 성능을 평가하는 지표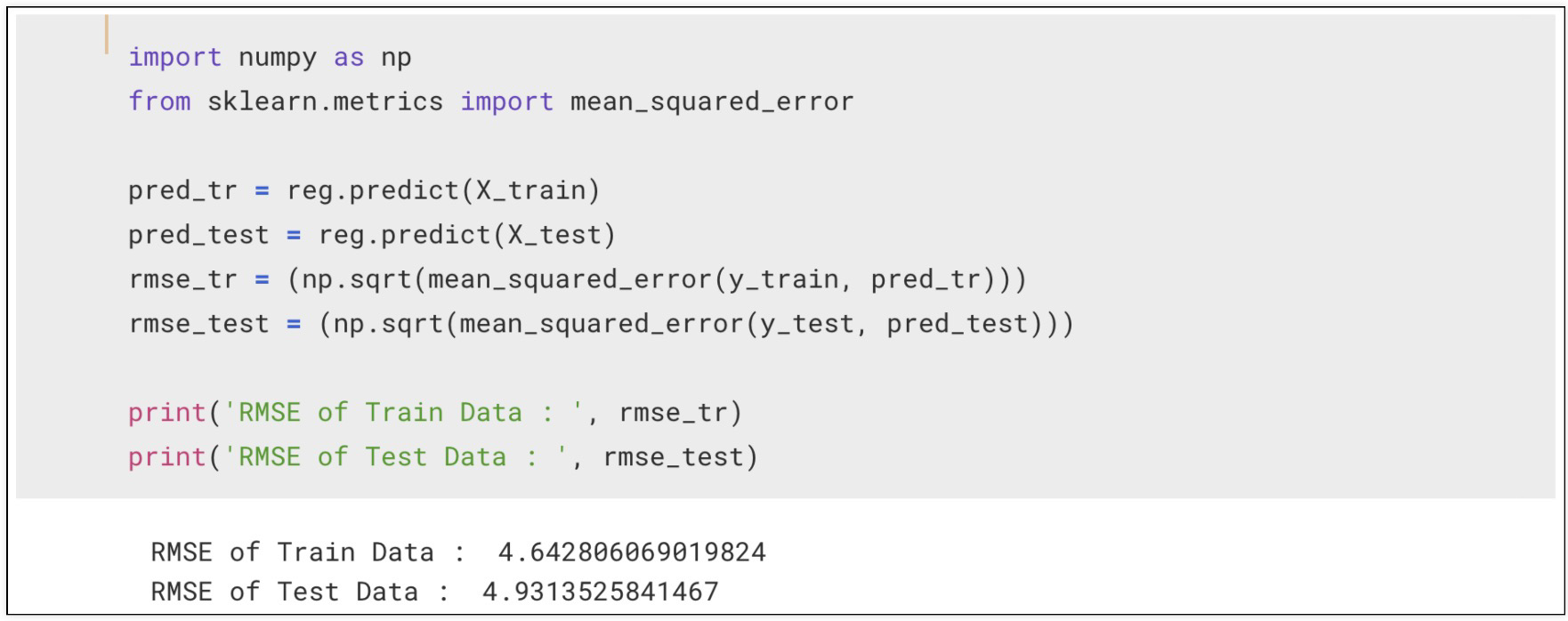
성능 확인

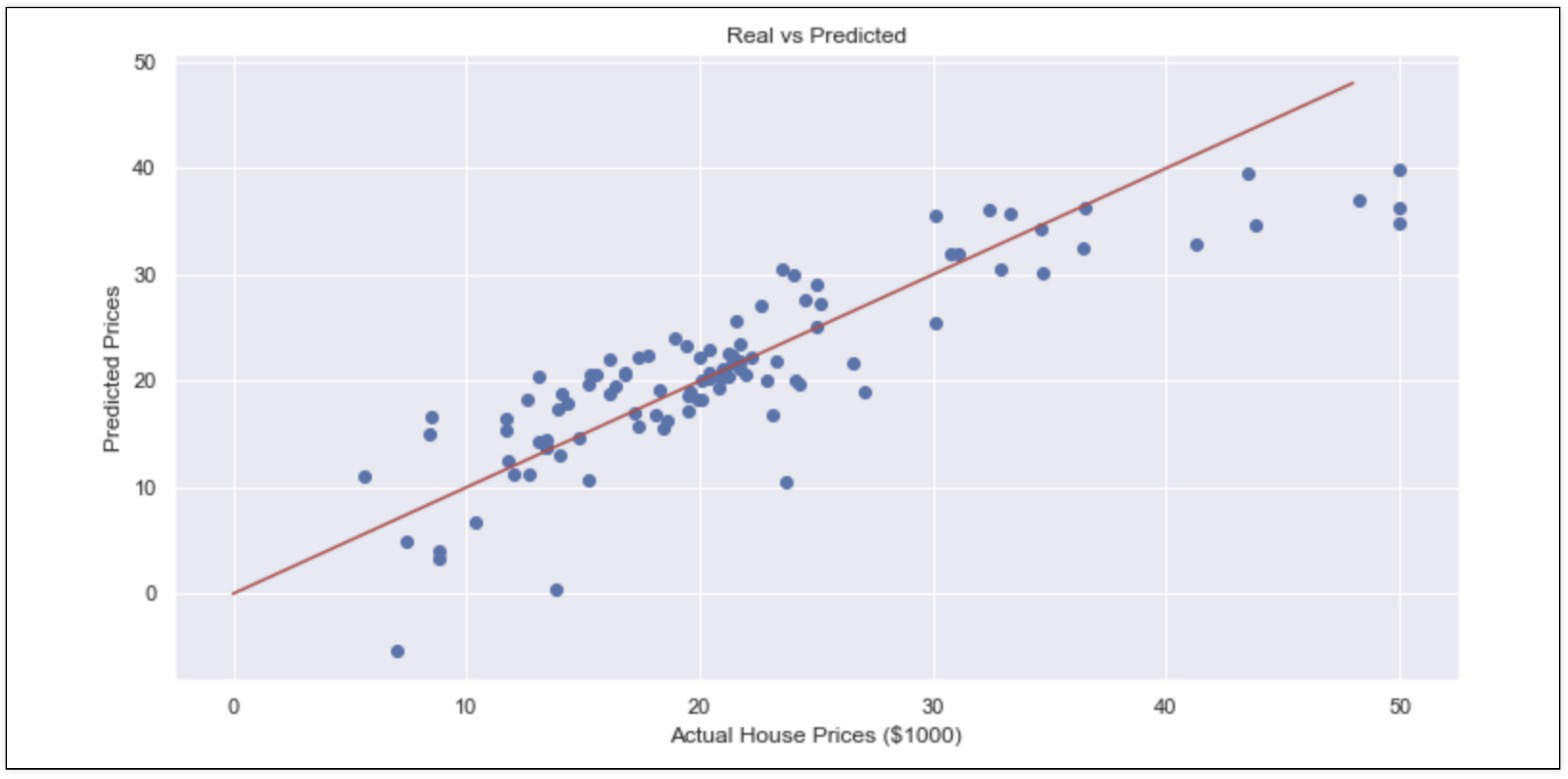
lstat(저소득층 인구)를 추가해서 모델 재확인

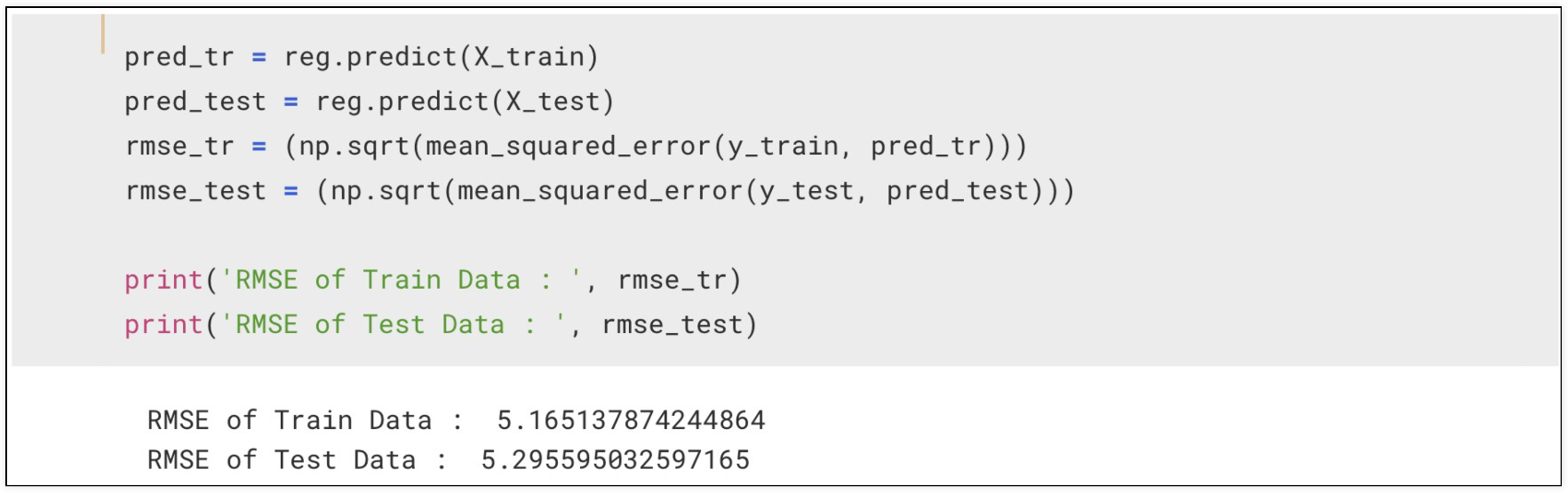
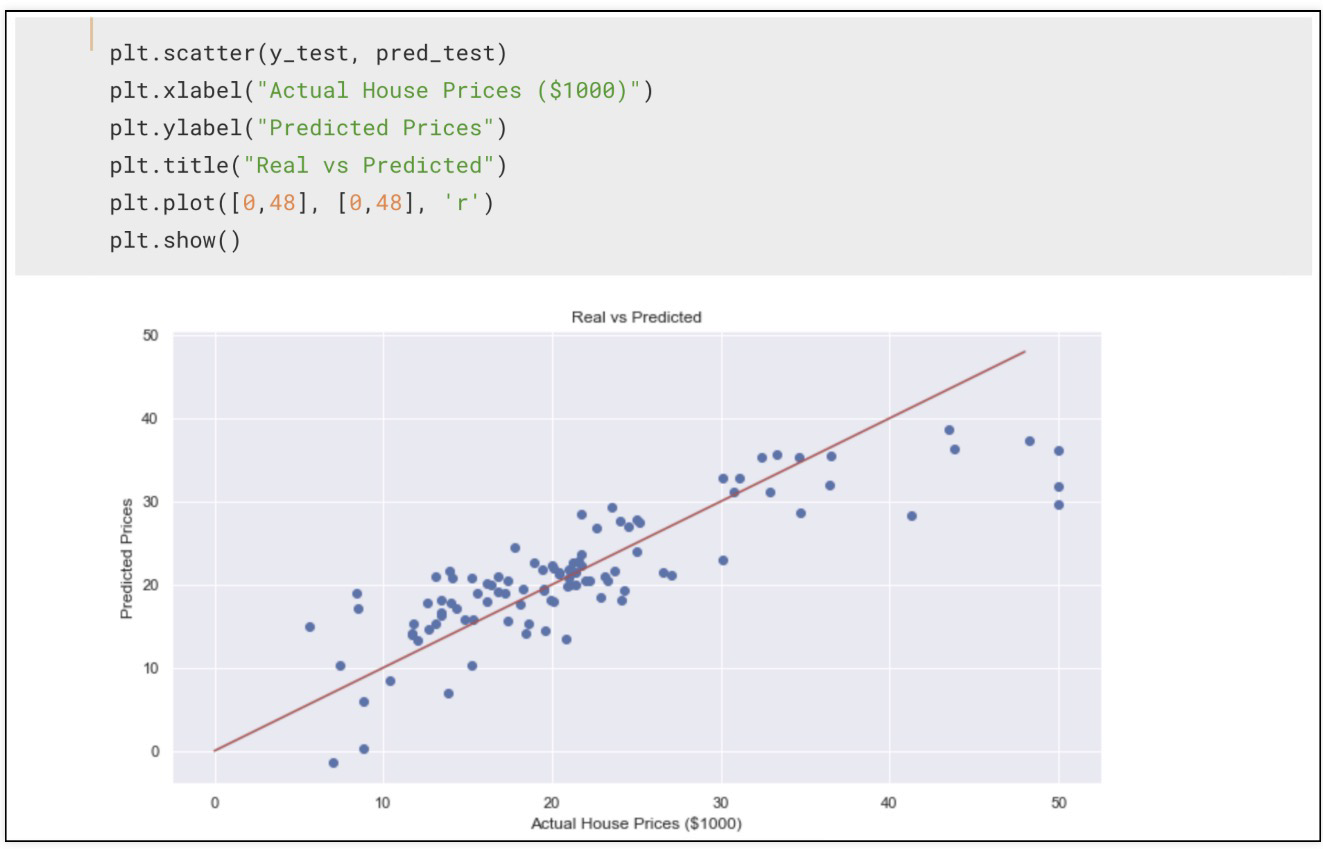
성능 나빠짐
따라서 매번 변수를 추가하여 확인하고, 어떤 변수가 포함/미포함 되어야하는지 고민 필요