BOJ 14853. 동전 던지기

문제 링크

동전 던지기의 결과를 알려주고, 동전이 앞면이 나올 확률에 대해 물어보는 문제라서 베이즈 정리를 활용할 수 있을 것 같았다!

결과적으로 베이즈 정리를 활용하여 확률분포를 구하고 적분을 통해 계산하는 것은 시간 초과가 나서 실패했지만, 그래도 계산 과정이 맞고 오랜만에 베이즈 정리 문제를 풀어봤으니까 이것도 써 봐야겠다!

베이즈 정리를 이용해서 확률 분포 구하기(시간 초과)

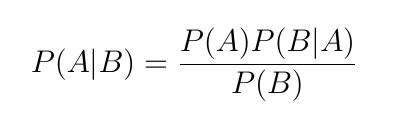
베이즈 정리의 모습인데, 여기서 동전의 확률 $p$와 $q$는 연속확률변수이므로 확률밀도함수에 대해서 쓰면 아래와 같다! 먼저 사건 $A$를 동전을 $n_1$번 던질 때 앞면이 $m_1$번 나온 사건으로 정의하고, 동전 1의 사전 확률 분포는 $f(x) = 1$이 된다. 우리가 구하고자 하는 것은, 사건 $A$가 발생했을 때의 사후확률분포로 다음과 같이 계산할 수 있다.

$f(x|A) = \frac{P(A|x)f(x)}{P(A)}$ = $\frac{_{n_1}C_{m_1}x^{m_1}(1-x)^{n_1-m_1}}{\int_{0}^1 {_{n_1}C_{m_1}x^{m_1}(1-x)^{n_1-m_1}}dx}$

동전 2의 경우도 식은 동일하고, $n_1$, $m_1$ 대신 $n_2$, $m_2$가 들어간다는 것과 $x$ 대신 $y$ 등과 같이 다른 문자를 사용한다는 점이 다를 것이다.

구하고자 하는 확률은 다음과 같이 계산될 것이다.

$P(p < q) = \int_{0}^{1} {\int_{0}^{q} {f(p|A) dp}} f(q|B) dq$

예제 입력 $n_1 = 2$, $m_1 = 1$, $n_2 = 4$, $m_2 = 3$에 대해 직접 계산한 결과는 다음과 같다.

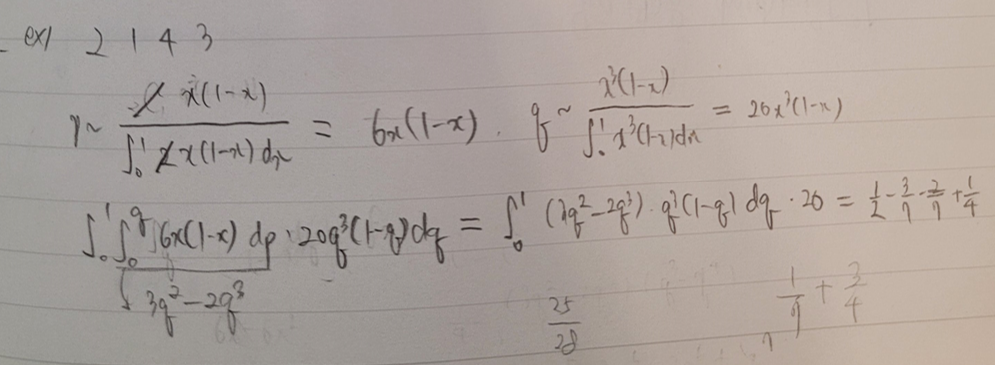
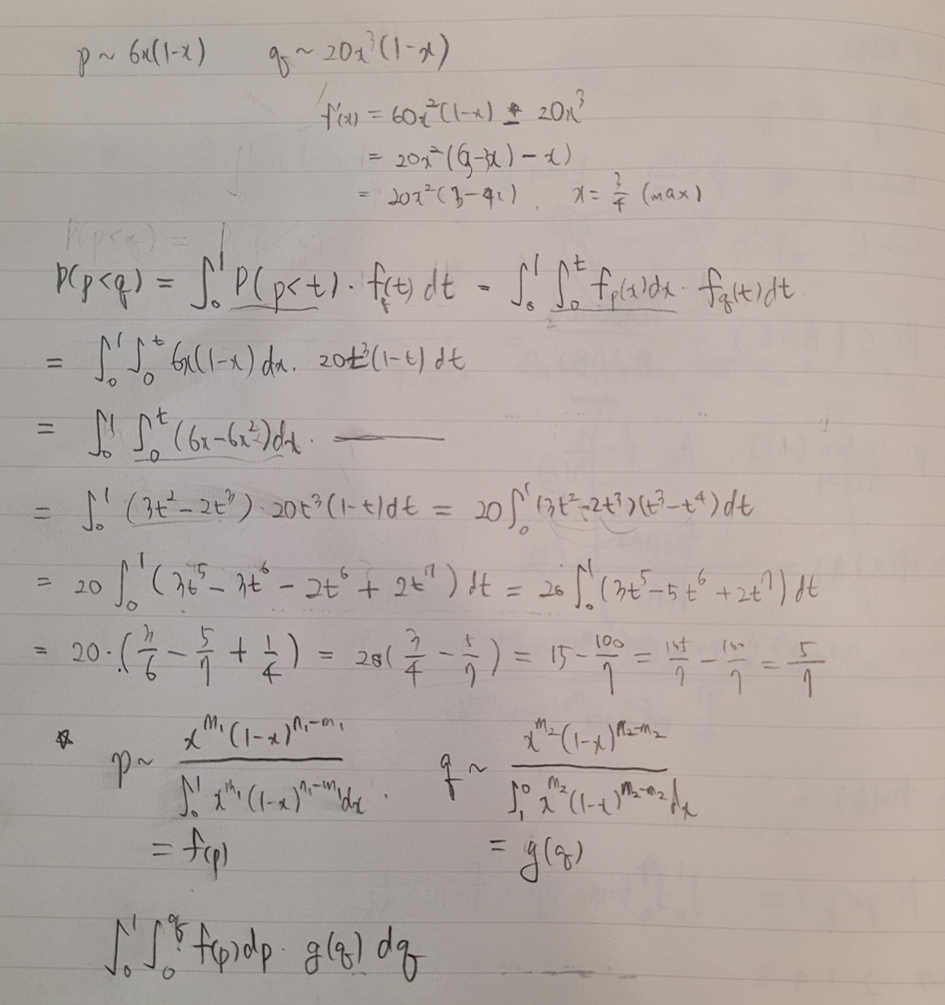
일반화하면 대충 이렇게 생겼는데, 안 하는 게 좋을 것 같다...

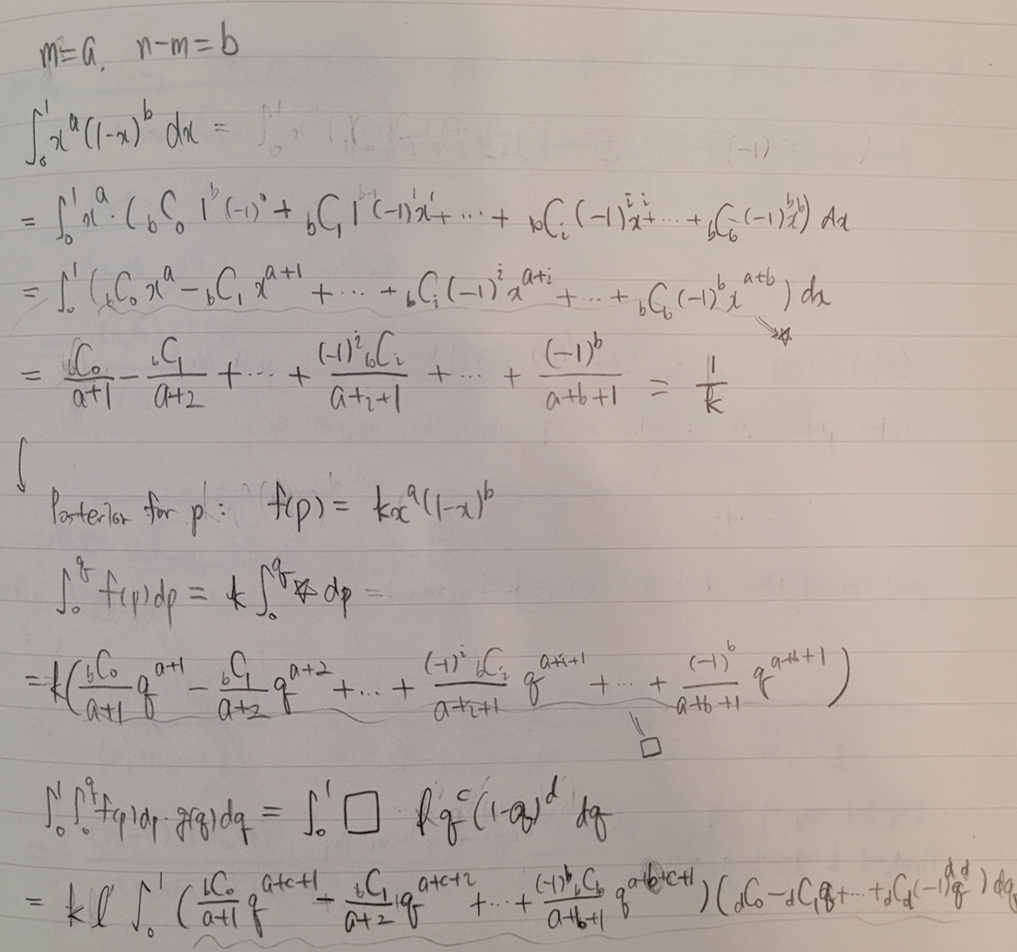
파이썬으로 이 내용을 구현하여 제출했더니 시간 초과가 발생했다.

# BOJ 14853. 동전 던지기

from math import comb
from decimal import *

def solve():
    # Input
    v = list(map(int, input().split()))
    n1, m1, n2, m2 = v[0], v[1], v[2], v[3]
    a, b, c, d = m1, n1 - m1, m2, n2 - m2
    # Get normalizing constants of posterior distribution of p and q
    k, l = Decimal(0), Decimal(0)

    for i in range(b + 1):
        k += Decimal(comb(b, i) * (-1) ** i) / Decimal(str(a + i + 1))

    for i in range(d + 1):
        l += Decimal(comb(d, i) * (-1) ** i) / Decimal(str(c + i + 1))

    # Let posterior distributions of p and q be f(p), g(q) each.
    # Then f(p) = (1 / k) * x^a * (1 - x)^b and g(q) = (1 / l) * x^c * (1 - x)^d.
    # First integrate f(p) from p = 0 to p = q. Let the result be F(q).
    # Then integrate F(q)g(q) from q = 0 to q = 1. This is the answer.
    answer = Decimal(0)
    for i in range(b + 1):
        for j in range(d + 1):
            term = Decimal(comb(b, i))
            term /= (Decimal(a + i + 1) * Decimal(a + i + j + c + 2))
            term *= Decimal(comb(d, j))
            term *= Decimal((-1) ** (i + j))
            answer += term
    answer *= Decimal(1 / k) * Decimal(1 / l)
    # Output
    print(answer)


getcontext().prec = 15
n = int(input())
for i in range(n):
    solve()

수직선 위에 점을 찍는 문제로 바꾸어 생각하기

한편, 이 블로그에 나온 방식으로 이 문제를 수직선 위에 점을 찍는 문제로 바꾸어 생각한다면 훨씬 간단한 방식으로 풀 수 있다! 뭔가 중복조합을 공부할 때 $_nH_r = _{n+r-1}C_r$라는 내용을 증명할 때 썼던 방식과 비슷해 보이는 것 같다.

$p$(또는 $q$)를 임의로 찾는 과정은, 수직선 $[0,1]$ 위에 임의로 점을 하나 찍는 것과 같고, 동전을 던지는 과정 역시 수직선 위에 점을 하나 찍어 $p$(또는 $q$) 왼쪽이면 앞면, 오른쪽이면 뒷면이라고 생각한다면 전체 과정은 수직선 위에 $(n_1 + n_2 + 2)$개의 점을 찍는 과정이라고 생각할 수 있다!

이때, 이 중 $(n_1 + 1)$개의 점을 선택하면, $m_1$이 정해져 있으므로 크기 순으로 $(m_1 + 1)$번째 점이 $p$가 될 것이고, 나머지 점 중 $(m_2 + 1)$번째 점이 $q$가 될 것이다.

즉, 전체 경우의 수는 $_{n_1+n_2+2}C_{n_1+1}$이 된다!

이제 $p<q$가 되는 경우를 구해야 한다. $p$ 왼쪽에는 최소 $m_1$개의 점이 있을 수 있고, 최대 $(m_1 + m_2)$개의 점이 있을 수 있다. 만약 $p$ 왼쪽에 $(m_1 + m_2)$개 이상의 점이 오게 된다면 $p>q$가 되기 때문이다. 즉, 각각을 경우로 나누어서 $m_1 \le k \le m_1 + m_2$에 대해 $p$ 왼쪽에 $k$개의 점이 있을 때, 그 중 $m_1$개를 선택하고 $p$ 오른쪽의 $(n_1 + n_2 + 1 - k)$개의 점 중 $(n_1 - m_1)$개의 점을 선택하는 경우의 수가 된다.

따라서 구하는 경우의 수는 $\displaystyle\sum_{k=m_1}^{n_1 + n_2 + 1 - k}{_{k}C_{m_1} × _{n_1 + n_2 + 1 - k}C_{n_1 - m_1}}$이다.

이를 제한 시간 내에 계산하기 위해서는 $k=m_1$일 때의 값을 변수에 저장한 뒤, 달라지는 값들만 추가적으로 계산해 주면 된다. 또한, 입출력이 많아 input() 과 print() 함수를 사용하지 않고 sys.stdin.readline() 과 sys.stdout.write() 함수를 사용했다.

# BOJ 14853. 동전 던지기

import sys


def solve():
    # Input
    v = sys.stdin.readline()
    v = list(map(int, v.split()))
    n1, m1, n2, m2 = v[0], v[1], v[2], v[3]
    # p and q follow uniform distribution, so it can be thought as picking one real number from [0, 1].
    # A toss of coin P (or Q) can be thought as picking one real number x from [0, 1],
    # considering the result 'head' if x > p (or q) and 'tail' otherwise.
    # Therefore, the problem can be reduced into picking (n1 + 1) points about coin P
    # among (n1 + n2 + 2) points, which are on number line [0, 1].
    # When (n1 + 1) points are chosen, left m1 points indicate head of coin P toss,
    # next one point indicates value of p, and last (n1 - m1) points indicate tail of coin P toss.
    # Remaining (n2 + 1) points can be labeled with the same rule about coin Q.
    # Consider point x = p on the line.
    # There can be m1 points at minimum and (m1 + m2) points at maximum, on the left.
    # If there are k(m1 <= k <= m1 + m2) points on the left,
    # we can choose m1 points among them and (n1 - m1) points among (n1 + n2 + 1 - k) points on the right about coin P.
    # Then, we can determine q uniquely, by finding (m2 + 1)-th point among remaining points from the left.
    # Here, p < q always holds.
    # To compute these values takes a lot of time, so first try to compute when k = m1 and reuse the value for other k.
    base = 1
    for i in range(0, n2 + 1):
        base = base * (n1 - m1 + 1 + i) / (n1 + 2 + i)
    answer = base
    # Here, when k = m1 + i, the desired value is base * (m1 + i) * (n2 + 2 - i) / i / (n1 + n2 - m1 + 2 - i).
    for i in range(1, m2 + 1):
        base *= (m1 + i) * (n2 + 2 - i) / i / (n1 + n2 - m1 + 2 - i)
        answer += base
    # Output
    sys.stdout.write(str(answer) + '\n')


n = int(input())
for i in range(n):
    solve()