
실제 그래프 vs 랜덤 그래프
랜덤 그래프
- 확률적 과정을 통해 생성한 그래프
- ex) Eros-Renyi Random Graph
Eros-Renyi Random Graph
- 임의의 두 정점 사이 간선이 존재하는지 여부는 동일한 확률 분포에 의해 결정됨
- G(n,p)로 표현되며, 1. n개의 정점을 가지고, 2. 임의의 두개의 정점사이에 간선이 존재할 확률은 p, 3. 정점간의 연결은 독립적이다.
작은 세상 효과
경로, 거리, 지름
경로(Path) : 정점 u,v사이의 경로는 아래 조건을 만족하는 순열(Sequence)
1. u에서 시작해서 v에서 종료
2. 순열에서 연속된 정점은 간선으로 연결되어야한다.
경로의 길이 : 해당 경로에 놓인 간선의 수
거리(Distance) : u와 v의 거리는 최단경로의 길이
지름(Diameter) : 그래프내의 정점간의 거리의 최대값
작은 세상 효과(Small-world Effect)
임의의 두 사람을 골랐을 때, 몇 단계의 지인을 거쳐 연결되어 있을까?
** 여섯 단계 분리(Six Degrees of Separation) 실험
- 사회학자 스탠리 밀그램에 의해 1960년대에 수행된 실험입니다.
- 오마하(네브라스카 주)와 위치타(켄사스 주)에서 500명의 사람을 뽑았습니다.
- 그들에게 보스턴에 있는 한 사람에게 편지를 전달하게끔 하였습니다.
- 단, 지인을 통해서만 전달하게끔 하였습니다.
결과적으로 25%의 편지만 도착했지만, 평균적으로 6단계만을 거쳤습니다.
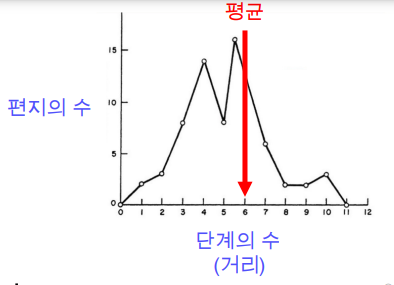
이러한 현상을 작은 세상 효과(Small-world Effect)라고 부릅니다.
작은 세상 효과는 높은 확률로 랜덤 그래프에서도 존재합니다.
하지만 모든 그래프에서 작은 세상 효과가 존재하는 것은 아닙니다.
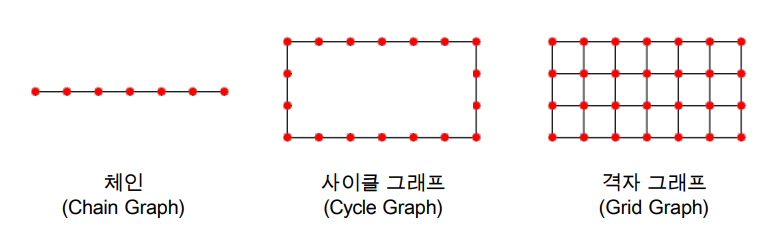
Chain, Cycle, Grid 그래프에서는 작은 세상 효과가 존재하지 않습니다.
연결성의 두터운 꼬리 분포
연결성
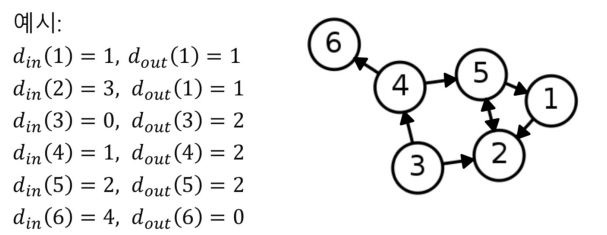
- 정점의 연결성(Degree)은 정점과 연결된 간선의 수를 나타냄
- 정점 v의 연결성은 d(v),dv,|N(v)|로 표현
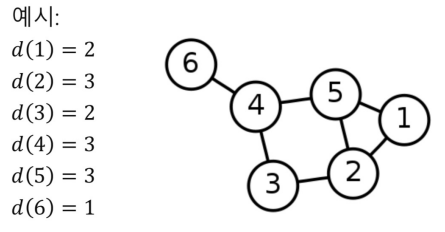
- Directed Graph의 경우 In/Out을 고려해서 표현
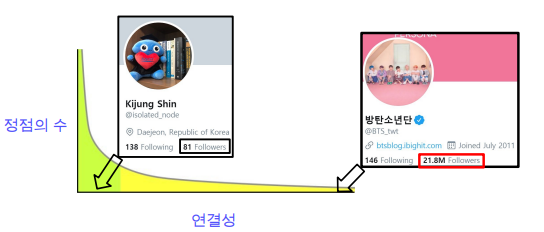
두터운 꼬리 분포
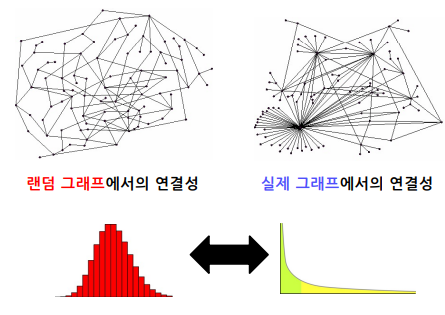
실제 그래프의 연결성 분포는 두터운 꼬리(Heavy Tail)를 갖습니다.
즉, 연결성이 매우 높은 허브(Hub) 정점이 존재함을 의미합니다.
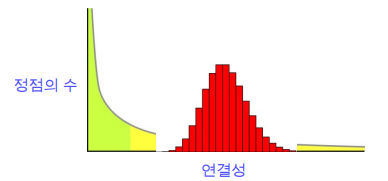
하지만, 랜덤 그래프의 연결성 분포는 높은 확률로 정규 분포와 유사합니다.
즉, 허브(Hub) 정점이 존재할 확률이 매우 낮습니다.
거대 연결 요소(Giant Connected Component)
연결 요소(Connected Component)
아래 조건들을 만족하는 정점들의 집합을 의미합니다.
1. 연결 요소에 속하는 정점들은 경로로 연결될 수 있습니다.
2. (1)의 조건을 만족하면서 더이상 정점을 추가할 수 없습니다.
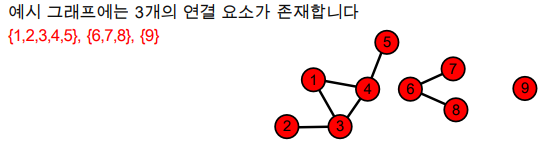
실제 그래프에서는 거대 연결 요소(Giant Connected Component)가 존재합니다
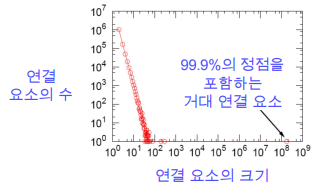
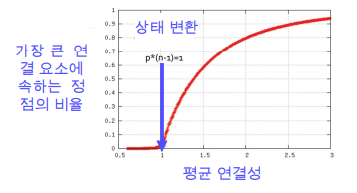
랜덤 그래프에서도 높은 확률로 거대 연결 요소가 존재합니다.
단, 정점들의 평균 연결성이 1보다 충분히 커야합니다.
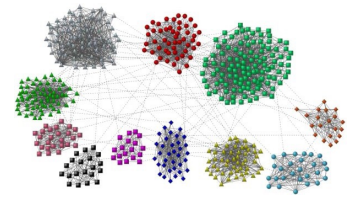
군집 구조
군집(Community) 이란 다음 조건들을 만족하는 정점들의 집합입니다.
1. 집합에 속하는 정점 사이에는 많은 간선이 존재합니다.
2. 집합에 속하는 정점과 그렇지 않은 정점 사이에는 적은 수의 간선이 존재합니다.
**지역적 군집 계수(Local Clustering Coefficient)는 한 정점에서 군집의 형성 정도를 나타냅니다.
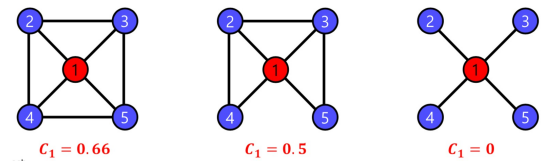
- 정점 i의 지역적 군집 계수는 정점 i의 이웃 쌍 중 간선으로 직접 연결된 것의 비율을 의미합니다.
- 정점 i의 지역적 군집계수는 Ci로 표현합니다.
- 단, 연결성이 0인 정점에서는 정의되지 않음
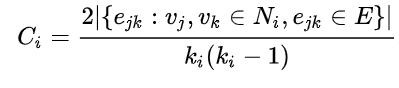
Ni: i의 이웃, E : 간선의 집합, ki : i의 이웃의 수
**전역 군집 계수(Global Clustering Coefficient)는 전체 그래프에서 군집의 형성 정도를 측정합니다.
그래프 G의 전역 군집 계수는 각 정점에서의 지역적 군집 계수의 평균입니다
실제 그래프에서는 군집계수가 높습니다. 즉, 많은 군집이 존재합니다
그 이유로 동질성, 전이성을 들수 있습니다.
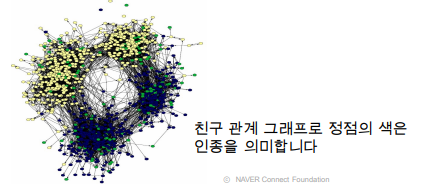
동질성(Homophily) : 서로 유사한 정점끼리 간선으로 연결될 가능성이 높습니다.
같은 동네에 사는 같은 나이의 아이들이 친구가 되는 경우가 그 예시입니다.
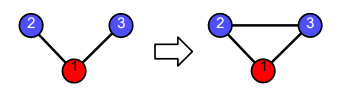
전이성(Transitivity) : 공통 이웃이 있는 경우, 공통 이웃이 매개 역할을 해줄 수 있습니다. 친구를 서로에게 소개해주는 경우가 그 예시입니다.
반면 랜덤 그래프에서는 지역적 혹은 전역 군집 계수가 높지 않습니다.
그 이유는 간선 연결이 독립적이기 때문입니다.
