File organization
Heap file
- 가장 단순한 file organization 으로 저장되는 순서대로 레코드를 저장
- Insert : Append
- Search : 원하는 레코드가 나올때까지 순차접근
- 삭제된 레코드가 차지하던 공간을 재사용하지 않아 주기적으로 재조직할 필요가 있음
- Insert 만 빠름
Sequential file
- 하나 이상의 필드값에 따라 순서대로 저장된 파일
- Insert : 레코드의 순서를 고려하여 수행
- Heap file 과 마찬가지로 삭제된 레코드 공간을 재사용하지 않아 주기적으로 재조직할 필요가 있음
- Search key에 대한 search는 효율적이나 이외의 필드를 탐색하는 것은 Heap file과 마찬가지로 순차접근
Index
Single level index
- 각 엔트리는 <탐색 키, 포인터> 로 구성
- 엔트리들은 탐색 키 값의 오름차순으로 정렬됨
- 하나의 파일에 여러개의 인덱스를 만들 수 있음(create index)
- 모든 속성에 대해 index를 만들 수 있다. 하지만 domain cardinality 가 낮은, 즉 가지는 값의 범위가 작은 속성에 대해 index를 만드는 것은 어리석은 방법
- 인덱스를 가지는 속성에 대해선 이진탐색으로 빠르게 search 할 수 있음
index의 종류
Clustering indexvsSecondary index
Clustering index: Search key에 따라 정렬된 데이터 파일에 대해 정의됨Secondary index: Search key에 의해 정렬되지 않은 데이터 파일에 대해 정의됨
Sparse indexvsDense index
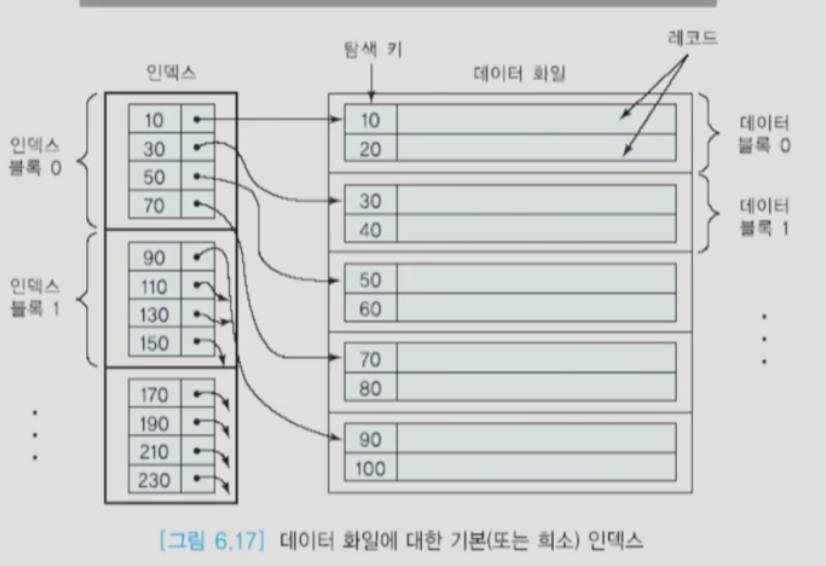
Sparse index: Clustering index인 경우 Search key 값에 대한 모든 정보를 인덱스 엔트리로 저장하지 않고 일부만 저장하는 것(보통 디스크 블럭의 첫번째 레코드에 대한 인덱스)Dense index: Search key 값에 대한 모든 정보를 인덱스 엔트리로 저장- Clustering index는 Sparse index가 될 수 있고 Secondary index는 무조건 dense index
- Sparse index가 더 공간 효율적이며 이로인해 index 탐색시 디스크 io가 dense index에 비해 적을 수 있음(sparse index가 대체로 효율적임)
- count 함수를 쓰는 경우 dense index를 쓰면 Index 접근만으로 질의가 가능.(dense index가 더 유리한 경우도 있음)
- 하나의 파일에 Sparse index는 최대 한개, dense index는 여러개 가질 수 있음
Primary inde
-
Primary key로 만든 인덱스로 데이터 file이 그 키 값에의해 정렬된 경우 정의됨
-
그래서 Primary index는 Clustering index이며 Clustering index이므로 Sparse index로 활용할 수 있음
Multi level index
-
인덱스 자체가 클 경우 인덱스를 탐색하는 시간도 오래 걸림
-
인덱스의 인덱스를 만듦. 이 과정을 가장 상위 단계의 인덱스가 하나의 블록에 들어갈 수 있을때 까지 반복하며 가장 상위 단계 인덱스를 마스터 인덱스라고 부름
-
마스트 인덱스는 한 블록으로 이루어지기 때문에(적은 공간을 차지하기 때문에) 주기억 장치에 상주할 수 있음
-
대부분 B+ 트리를 사용
-
B+ 트리(balanced tree) : root 에서 leaf 까지 거리가 균일, 모든 노드들이 가지는 자식의 개수가 일정한 범위 내에 있음 , 반대 skewed tree
-
검색에 대해선 효율적임. 하지만 데이터의 구성이 바뀌게 되면 index를 변경해줘야하는 index maintenanace overhaed가 발생
SQL의 인덱스 정의문
- SQL의 CREATE TABLE 문에서 PRIMARY KEY로 명시한 속성에 대해서는 자동적으로 Primary index가 생성
- UNIQUE로 명시한 속성에 대해서는 Secondary index를 생성
- 다른 속성에 대해서 index를 정의하는 SQL의 표준이 존재하지 않아 DBMS마다 다르다
- 인덱스를 꼭 하나의 속성으로 만들 필요가 없음
- Ex) CREATE INDEX EmpIndex ON EMPLOYEE (DNO,SALARY);
- 하지만 다중 컬럼 인덱스를 만들 경우 첫번째 인덱스(여기서는 DNO)를 포함하지 않고 Where절에 단독으로 사용될 경우 인덱스를 활용하지 못함(order by 1,2,3,4..로 되어있어서 그런듯)
인덱스의 장단점
- 장점
- 검색속도 향상
- 릴레이션이 매우 크고, 질의에서 릴레이션의 튜플들 중에 일부(2~4%)를 검색하고 WHERE절이 잘표현되었을때 특히 성능에 도움이 됨
- 단점
- 저장공간 차지
- 삽입, 삭제, 수정 연산의 속도를 저하시킴
인덱스 선정 지침
- 기본 키는 클러스터링 인덱스를 정의할 훌륭한 후보
- 외래 키도 인덱스를 정의할 중요한 후보
- 속성의 유니크한 값이 전체 레코드 수와 비슷하고 동등 조건으로 사용되면 비 클러스터링 인덱스를 생성하는 것이 좋음
- 튜플이 많이 들어 있는 릴레이션에서 대부분의 질의가 검색하는 튜플이 2~4% 미만일 경우 인덱스 생성
- 자주 갱신되는 속성은 인덱스를 정의하지 않는 것이 좋음
- 갱신이 자주 일어나는 릴레이션에는 인덱스를 많이 만드는 것을 피함
- 후보 키는 기본 키가 갖는 모든 특성을 마찬가지로 갖기 때문에 인덱스를 생성할 후보
- 정수형 속성에 인덱스를 생성
- Varchar 는 인덱스를 만들지 않음
- 작은 파일에는 인덱스를 만들 필요가 없음
- 대량의 삽입을 할때는 인덱스를 모두 제거하고 데이터 삽입이 끝난 후에 인덱스들을 다시 생성하는 것이 좋음
- Order by, group by에 자주 사용되는 속성은 인덱스를 정의할 후보
인덱스가 사용되지 않는 경우
- 시스템 카탈로그가 오래 전의 데이터베이스 상태를 나타냄(시스템 카탈로그는 보통 주기적으로 업데이트)
- DBMS의 질의 최적화 모듈이 릴레이션의 크기가 작아서 인덱스가 도움이 되지 않는다고 판단함
- 인덱스가 정의된 속성에 산술 연산자, 내장 함수가 사용되는 경우
- NULL값에 대해서 search 할때 사용되지 않음
질의 튜닝을 위한 지침
- DISTINCT절의 사용을 최소화하라
- GROUP BY , HAVING을 최소화 하라
- 임시 릴레이션의 사용을 피하라
- SELECT * 대신에 SELECT 절에 애트리뷰트 이름들을 구체적으로 명시하라
B-tree
B-treee는 Balanced tree의 약자로 root node에서 leaf node 까지의 거리가 모두 같으며, 각 node는 최소한 가져야하는 key의 개수가 존재하여 어느정도 균일한 개수의 key를 가지는 tree이다.
B-tree는 Order를 가지며 이 Order는 정의하는 방식이 다양하다. 여기서 소개할 방식은 Order를 하나의 Node가 구분할 수 있는 영역의 최대 개수로 정의한다. 예를 들어 2진트리의 경우 이 값이 2가 된다.
root node : 최상단의 node로 unique하다
leaf node : 최하단의 node
internal node : leaf node와 root node 사이에 존재하는 node
B-tree의 성질
- leaf node를 제외한 모든 Node는
자식의 수=key의 수-1를 만족함 - 모든 node는 최대 M개의 자식, M-1개의 key를 가짐 (M : B-tree의 order)
- Internal node는 최소 ceil(M/2)개의 자식, ceil(M/2)-1개의 key를 가짐 (ceil : 올림)
- leaf node는 최소 ceil(M/2)개의 자식을 가짐
B-tree 의 insert
- tree에서 삽입하려는 값이 어떤 leaf node에 삽입되어야하는지 찾고, 해당 값을 leaf node에 삽입한다.
- 만약 해당 node가 M개이상의 key를 가지게 되면 중간값을 부모노드로 승급시키고 중간값을 기준으로 2개의 node로 split한다. 해당 node가 root노드일 경우 중간값을 가지는 새로운 node를 만들고 그 node를 root node로 변경
- 만약 2번 과정을 통해 특정 node가 M개 이상의 key를 가지게 되면 해당 node에 대해 2번과정을 수행한다.
B-tree 의 delete
- 삭제한 key가 leaf node의 값이 아닌 경우 해당 값의 왼쪽 가지의 가장 우측 값을 뺏아옴
- 삭제한 key가 leaf node의 값인 경우, 혹은 1번 과정을 거쳐 leaf node의 값이 삭제된 경우, 만약 leaf node의 key값의 개수가 ceil(M/2)-1 보다 작아지면 해당 node의 parent node의 key 값중 child node의 key의 개수가 많은 key(같으면 왼쪽 key)를 강등시키고 강등된 key에 인접한 child node를 병합시킨다.
- 만약 key를 빼앗긴 node가 key값의 개수가 ceil(M/2)-1 보다 작다면 2번과정을 이 node의 Key에대해 수행, 하지만 만약 이 node가 root node인 경우 완료. 만약 Root node에 key가 모두 제거되면 root node의 child node를 root node로 변경
B+tree
- B+tree는 B-tree 와 다르게 leaf node에 모든 값을 유지하며 leaf node를 linked list로 연결
- B-tree의 노드는 데이터(key에 해당하는 disk로의 포인터)를 가진다. 반면 B+tree는 leaf node 에만 데이터를 가진다.
- B+tree는 insert 와 delete가 leaf node에서 일어난다.
B+tree의 장점: Full scan 시에 tree를 순회할 필요 없이 leaf node만 순차접근하면된다. leaf node에만 데이터를 가지므로 정보를 더 컴팩트하게 저장할 수 있다.B+tree의 단점: B-tree의 최적의 경우는 root node에서 key를 발견하는 경우지만 B+tree는 항상 leaf node까지 가야한다.(leaf node에 데이터가 있기때문)
