크루스칼(Kruskal) 알고리즘!!!!!!!
이다..(인접 리스트에 대한 크루스칼 알고리즘)
일단 크루스칼 알고리즘은 최소신장트리를 만드는 알고리즘 중 하나인데,
간선에 대한 가중치를 기준으로 가장 작은 값부터 차례대로 진행하는 알고리즘이다.
간략하게 크루스칼 알고리즘을 구현하는 순서에 대해서 먼저 메모!
- 메인함수(시작 함수)
여기서 부모 노드를 설정해준다.(초기 값은 자기 자신과 동일하게 잡는다.)
이후 edges(그래프)을 정렬하고 값들을 담아준다.
최소 신장 트리를 작성할 때, 싸이클이 형성되면 안되기 때문에 만들어둔 부모 노드 배열을 기반으로 싸이클이 형성되는지를 판별해준 후 싸이클이 형성되지 않는 경우에 union을 해준다.
이렇게 작성하기 위해서 필요한 함수는 두 가지이다.
첫 번째는 부모 노드의 값을 찾아주는 함수,
두 번째는 그래프의 각 노드를 연결해주는 과정(여기서는 부모 노드로 확인한다.)
일단 메인 함수는 다음과 같다.
//edges는 노드1번, 노드2번, 가중치 순서로 담긴 배열이다.
//node는 그래프에 속한 노드의 개수이다.
function kruskal(edges, node) {
const n = node;
//부모 노드 배열을 만들고 자기 자신을 담아준다.
const pNode = [];
for (let i = 0; i <= n; i++) {
pNode.push(i);
}
//가중치가 작은 것 부터 차례대로 정렬
edges = edges.sort((a, b) => a[2] - b[2]);
//cost 안에 최소 신장트리가 만들어지고 지나온 경로에 해당하는 가중치를 담아 줄 예정이다.
let cost = 0;
for (let i = 0; i < edges.length; i++) {
//edges를 돌면서 구조분해할당으로 a(노드1번), b(노드2번), c(가중치) 값을 담아준다.
const [a, b, c] = edges[i];
//findPnode함수를 거쳐서 비교할 대상의 최상위 부모 노드의 값이 같은지 다른지 확인해준다.
if (findPNode(pNode, a) !== findPNode(pNode, b)) {
//uniNode 함수 실행
uniNode(pNode, a, b);
cost += c;
}
}
return cost;
}다음은 findPNode 함수를 작성!
pNode[인자] 값과 그냥 인자값이 같은지 확인하고 같지 않다면,
재귀함수를 반복적으로 실행하여 같아질 때까지 반복한다.
function findPNode(pNode, x) {
//pNode[x]값과 x가 같은지 확인하여 같지 않을 경우 재귀
if (pNode[x] !== x) {
pNode[x] = findPNode(pNode, pNode[x]);
}
return pNode[x];
}마지막으로 union!
바꿔주어야하는 pNode 값은 인자로 넘어올 a, b 에 해당하는게 아니라
a, b를 기반으로 최상위 부모 노드의 위치를 확인하고 해당 노드를 수정해주어야 한다.
function uniNode(pNode, a, b) {
//각 변수에 findPNode값을 담아준다.
let pN1 = findPNode(pNode, a);
let pN2 = findPNode(pNode, b);
//두 값 중 값이 큰 pNode값에 작은 pNode값을 담아준다.
pN1 > pN2 ? (pNode[pN1] = pN2) : (pNode[pN2] = pN1);
}이렇게 로직 구현이 끝났고 그래프를 넣어서 확인하면 다음과 같다.
const edges = [
[1, 2, 15],
[1, 3, 6],
[2, 3, 27],
[2, 4, 16],
[3, 4, 8],
];
라는 그래프가 존재 할 때 일단 가중치를 기준으로 정렬해주면 다음과 같다.
const edges = [
[1, 3, 6],
[3, 4, 8],
[1, 2, 15],
[2, 4, 16],
[2, 3, 27],
];이 상태에서 pNode의 변화를 기술해보면 다음과 같다.
최초 pNode 상태
[0, 1, 2, 3, 4]
1번과 3번 노드를 확인하는데 각각 pNode[x]와 x값이 같으므로 각각 1, 3을 반환
그 후 더 작은 값인 1을 pNode의 3번 인덱스에 넣어준다.
[0, 1, 2, 1, 4]
3번과 4번 노드를 확인하는데 pNode[3]의 경우 값이 1이다. 3과 같지 않으므로
findPNode(pNode, 1)로 재귀를 실행하면
pNode[1]값은 1이므로 1을 반환한다.
4번 노드의 경우 pNode[4]와 4가 같으므로 4 반환
이후 uniNode함수에서 1이 4보다 작기 때문에 다음과 같이 나온다.
[0, 1, 2, 1, 1]
1번과 2번 노드를 확인 => 1과 2가 각각 반환
=> 1이 더 작으므로
[0, 1, 1, 1, 1]
2번과 4번 노드를 확인 => 1과 1이 반환
값이 같기 때문에 uniNode함수를 수행하지 않는다.
(kruskal함수의 부모값을 비교하는 로직에서 성립하지 않는다.)
[0, 1, 1, 1, 1]
2번과 3번 노드를 확인 => 1과 1이 반환
마찬가지로 uniNode함수를 수행하지 않음
최종적으로 pNode는 [0, 1, 1, 1, 1]이 되고
uniNode가 실행되었던 가중치를 모두 더하면
6 + 8 + 15 = 29
cost는 29를 반환하게 된다.
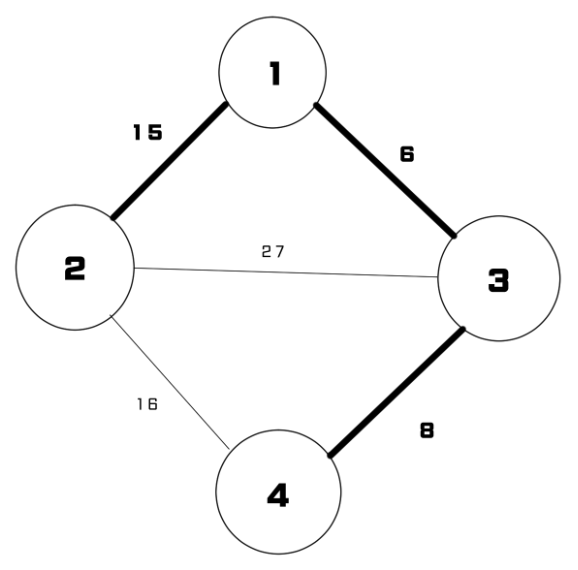
그림으로도 그려보았다.
전체 그래프의 모습에서 크루스칼 알고리즘에 선택된 간선은 굵은 실선으로 표시하였다.
알고리즘을 참고한 블로그 주소이다!
https://nohack.tistory.com/137
여러 알고리즘에 대한 로직이 있어서 앞으로도 신세를 많이 질 예정이다...