MF, ALS란?

유상준·2022년 10월 16일

ALS Collaborative Filtering DL Matrix Factorization recsys

Collaborative Filtering for Implicit Feedback Datasets 논문 내용 정리 + 관련 강의 내용 정리

1. Collaborative Filtering 기반 추천 시스템이란?

유저 A와 비슷한 취향을 가진 유저들이 선호하는 아이템을 추천
아이템이 가진 속성을 사용하지 않으면서도 높은 추천 성능을 보임

Collaborative Filtering 분류

1.Neighborhood-based CF(Memory-based CF)

User-based
Item-based

두가지 방법으로 분류 되며, 유저(아이템)간 유사도를 계산한 뒤, 타겟 유저(아이템)와 가장 높은 유사도를 지닌 유저(아이템)가 선호하는 아이템을 추천해준다.
모든 유저(아이템)간 유사도를 구해야 하므로, 유저와 아이템의 개수가 증가 할 수록 연산량이 높아지는 단점이 있다.

2. Model-based CF

항목 간 유사성을 비교하는 것에서 벗어나, 데이터에 내재한 패턴을 이용하여 추천하는 CF 기법 (Parametric Machine Learning 을 사용한다)
잠재적 특성이나 패턴을 찾아내 추천에 이용하는 원리
- Non-parametric(KNN, SVD)
- Matrix Factorization
- Deep Learning

세가지 정도의 방법으로 분류 되며, Neighborhood-based CF의 단점들을 해결하기 위해 구상되었다.

NBCF의 단점, 한계
1. Sparsity(희소성) 문제

데이터가 충분하지 않다면 추천 성능이 떨어진다. (유사도 계산이 부정확함)

데이터가 부족하거나 혹은 아예 없는 유저, 아이템의 경우 추천이 불가능하다. (Cold start)

2. Scalability(확장성) 문제

유저와 아이템이 늘어날수록 유사도 계산이 늘어난다.

유저, 아이템이 많아야 정확한 예측을 하지만 반대로 시간이 오래 걸린다.

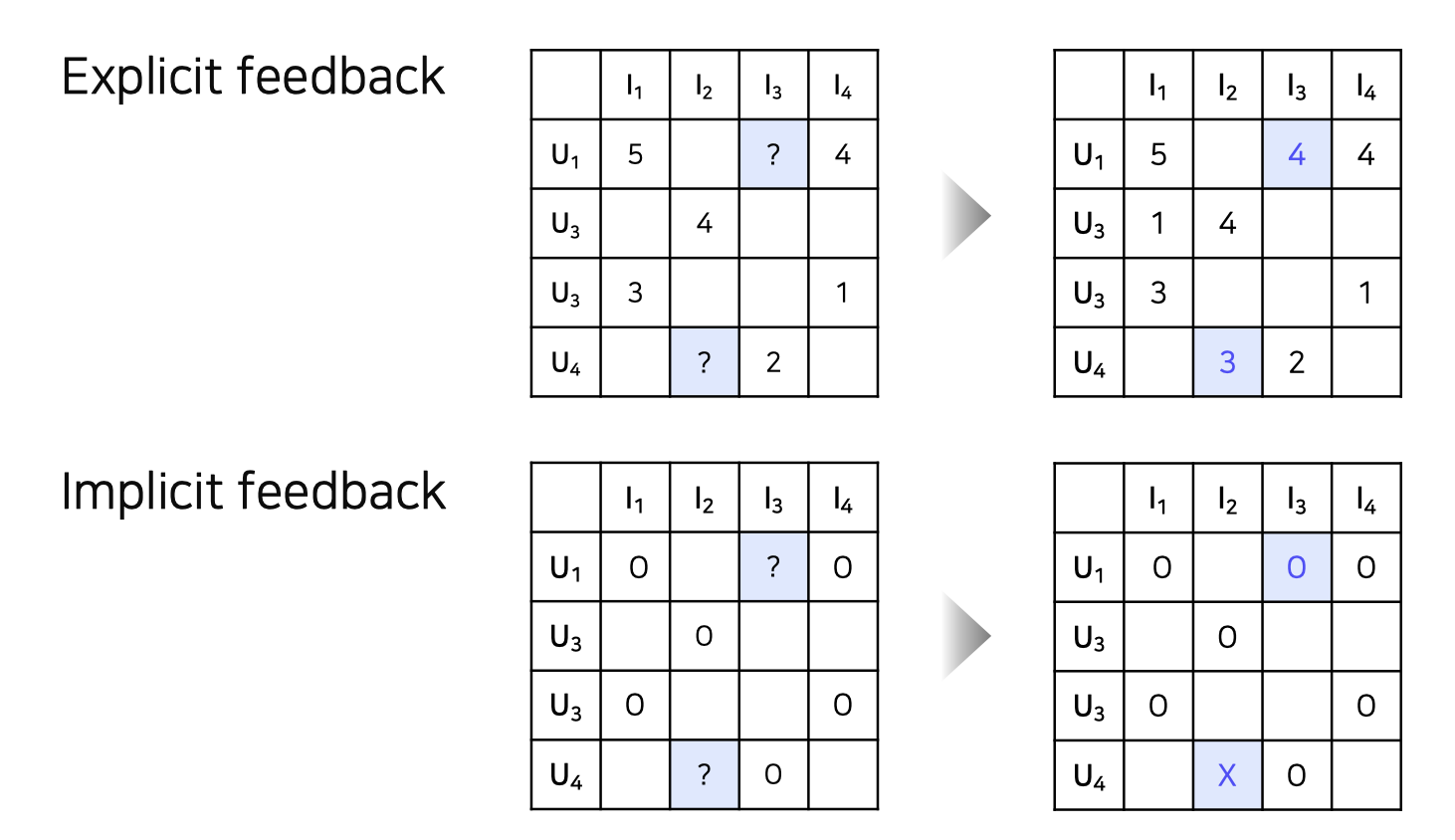
Explicit Data vs Implicit data

Explicit feedback
영화 평점, 맛집 별점 등 item에 대한 user 의 선호도를 직접적으로 알 수 있는 데이터 지난 강의에서 다룬 문제는 Explicit feedback 문제

Implicit feedback
클릭 여부, 시청 여부 등 item에 대한 user 의 선호도를 간접적으로 알 수 있는 데이터 유저-아이템 간 상호작용이 있었다면 1 (positive) 을 원소로 갖는 행렬로 표현 가능 현실에서는 implicit feedback 데이터의 크기가 훨씬 크고 많이 사용 됨

2. MF(Matrix Factorization)란?

User-Item 행렬을 저차원의 User와 Item의 latent factor 행렬의 곱으로 분해하는 방법
Rating Matrix( $R$ )를 P와 Q로 분해하여 $R$ 과 최대한 유사하게 $\hat{R}$ 을 추론(최적화)
$\hat{R} = P \times Q^T$
Objective Function을 최소화 하는 방향으로 학습한다. ( $p_u, q_i$ 에 대해 SGD)

true rating : $r_{u,i}$
predicted rating : $\hat{r_{u,i}} = p_u^Tq_i$
Objective Function : $\min_{P,Q}\sum_{\text{observed }r_{u,i}}(r_{u,i} - p_u^Tq_i)^2$

이 때, Objective Function에 규제 항을 추가하여 Overfitting을 방지해 주는 것이 성능 개선에 도움된다. 규제 항은 user vector와 item vector의 L2 norm으로 이루어져 있다.

Objective Function with L2 norm
$\min_{P,Q}\sum_{\text{observed }r_{u,i}}(r_{u,i} - p_u^Tq_i)^2 + \lambda(||p_u||_2^2 + ||q_i||_2^2)$

또한, 특정 유저의 편향 혹은 특정 아이템의 편향을 고려하기 위해 전체 평균, 유저/아이템 bias항을 추가하여 예측 성능을 높이기도 한다.

Objective Function with L2 norm and bias
$min_{P,Q}\sum_{\text{observed }r_{u,i}}(r_{u,i} - \mu - b_u - b_i - p_u^Tq_i)^2 + \lambda(||p_u||_2^2 + ||q_i||_2^2 +b_u^2+b_i^2)$
이 때, error와 업데이트 할 bias와 vector는 다음과 같다.
$e_{ui} = r_{u,i} - \mu - b_u - b_i - p_u^Tq_i$ $b_u = b_u + \gamma \cdot(e_{ui}-\lambda b_u)$ $b_i = b_i + \gamma \cdot(e_{ui}-\lambda b_i)$ $p_u = p_u + \gamma \cdot(e_{ui}q_i-\lambda p_u)$ $q_i = q_i + \gamma \cdot(e_{ui}p_u-\lambda q_i)$

3.ALS(Alternative Least Square)란?

왜 ALS를 사용하는가?

MF 방식에서 학습하는 과정인 SGD보다 Sparsity Data에 Robust하며, 대용량 데이터를 병렬 처리하며 학습할 수 있다는 장점이 있다.
또한, SGD는 두개의 행렬인 $P$ 와 $Q^T$ 의 곱연산으로 이루어지기 때문에, Non-Convex한 문제가 되는데, ALS는 한 행렬을 상수로 고정하고 연산하기 때문에 Convex한 문제로 전환이 가능하고 그 때문에 Global Minimum으로 수렴하기 쉽다
Convexity 참고 사이트

작동 원리

유저와 아이템 매트릭스를 번갈아가면서 업데이트 하는 아이디어를 사용한다
두 매트릭스 중 하나를 상수로 취급하고 나머지 매트릭스를 업데이트 한다.
즉, $p_u, q_i$ 가운데 하나를 고정한 뒤 나머지 하나로 least-square 문제를 해결하는 방식이라 하여 ALS라는 이름이 붙게 되었다.

Objective Function of ALS
$\min_{P,Q}\sum_{\text{observed }r_{u,i}}(r_{u,i} - p_u^Tq_i)^2 + \lambda(||p_u||_2^2 + ||q_i||_2^2)$

기본적인 수식은, MF의 목적함수와 동일해 보이나 $p_u$ 와 $q_i$ 를 차례로 번갈아 업데이트 하는 방식이 다르다.
$p_u, q_i$ 를 업데이트 하는 수식은 다음과 같다.

$p_u = (Q^TQ + \lambda I)^{-1}Q^Tr_ u$ $q_i = (P^TP + \lambda I)^{-1}P^Tr_ i$

Implicit Feedback을 고려

Preference

논문에서는, 유저 u가 아이템 i를 선호하는지의 여부를 아래와 같이 binary하게 표현한다
$f_{ui}= \begin{cases} 1, & \text{if } r_{ui}>0 \\ 0, & \text{if } r_{ui}=0 \end{cases}$

Confidence

유저 u가 아이템 i를 선호하는 정도를 나타내기 위하여, positive feedback과 negative feedback 간의 상대적인 중요도의 차이를 두기 위한 하이퍼 파라미터 $\alpha$ 를 이용해 표현한다.
$c_{ui} = 1 + \alpha \cdot r_{ui}$

위의 Preference와 Confidence를 고려하면서 바뀌게된 각 행렬( $P,Q$ )의 업데이트 값은 다음과 같다

$p_u = (Q^TC^uQ + \lambda I)^{-1}Q^TC^u f_u$ $q_i = (P^TC^iP + \lambda I)^{-1}P^TC^i f_i$
m is the number of users and n is the number of items

For each user u, let us define the diagonal n × n matrix $C^u$ where $C^u_{ii} = c_{ui}$

For each item i, let us define the diagonal m × m matrix $C^i$ where $C^i_{uu} = c_{ui}$

$p(u) ∈ R^n$ that contains all the preferences by u (the $f_{ui}$ values)

$p(i) ∈ R^m$ that contains all the preferences by i (the $f_{ui}$ values)

Explaining recommendations

이해도 부족 파트

이 논문에서는 위에서 나왔던 수식을 이용하여 사용자의 선호도를 설명할 수 있다고 주장한다.
유저 u의 아이템 i에 대한 선호도는 $\hat{f_{ui}} = q_i^T p_u$ 로 추정할 수 있는데,
이 때의 $p_u$ 자리에 위의 식( $p_u = (Q^TC^uQ + \lambda I)^{-1}Q^TC^uf_u)$ 을 대입하면
$\hat{f_{ui}} = q_i^T(Q^TC^uQ + \lambda I)^{-1}Q^TC^uf_u$ 라는 식이 탄생한다.
바로 위에 탄생한 식에서 잠재 벡터 차원을 $k$ 라고 한다면, $(Q^TC^uQ + \lambda I)^{-1}$ 는 $k \times k$ 행렬이 되고, 이를 유저 u의 weighting matrix $W^u$ 로 칭한다.
결국 아이템 i에 대한 user j의 $s^u_{ij} = q_i^TW^uq_{j\cdot}$ 로 표현된다. $(q_{j\cdot} = Q^TC^uf_u$ , $k\times1$ 벡터)
items
최종적으로 유저 u의 아이템 i에 대한 선호도 예측치는 $\hat{f_{ui}} = \sum\limits_{j:r_{uj} > 0} s^u_{ij}c_{uj}$ 로 표현된다.
이때, $s^u_{ij}$ 는 아이템간의 유사도, $c_{uj}$ 는 유저가 해당 아이템에 대해서 얼마나 신뢰성을 보이는지에 대한 정도로 이해할 수 있다.