🤷🏻♀️ 시간복잡도(Time Complexity)란?
-
알고리즘에서 시간복잡도는 [ 주어진 문제를 해결하기 위한 연산 횟수 ] 를 의미합니다.
-
시간복잡도와 로직 수행 시간은 비례하므로 시간 복잡도 수치가 작을수록 효율적인 알고리즘임을 뜻합니다.
-
파이썬에서는 2000만 번 ~ 1억 번의 연산을 1초의 수행 시간으로 예측 가능합니다.
📌 시간 복잡도 표기법( 점근 표기법 )
-
빅 오메가(Big - Ω) [ best case ]
최선일 때의 연산횟수를 나타낸 표기법
-
빅 세타(Big - θ) [ average case ]
보통일 때의 연산횟수를 나타낸 표기법
-
빅 오(Big - O) [ worst case ]
최악일 때의 연산횟수를 나타낸 표기법
🖥️ 시간복잡도 예제 코드
import random
findNumber = random.randrange(1, 101)
for i in range(1, 101) :
if i == findNumber :
print(i)
break위의 코드는 1~100 사이의 무작위값을 찾아 출력하는 코드입니다.
이 코드에서 빅 오메가(Big - Ω)표기법의 시간복잡도는 1번, 빅 세타(Big - θ)표기법의 시간 복잡도는 N/2번, 빅 오(Big - O)표기법의 시간 복잡도는 N번이라 할 수 있습니다.
👍🏻 알고리즘 풀이에 적합한 시간 복잡도는?!
코딩테스트에서는 수행시간을 최악일 때의 연산횟수를 나타내는 표기법인 빅 오(Big - O) 를 기준으로 계산하는 것이 가장 좋습니다.
Why? 코드를 작성하다보면 최선보다는 최악의 경우를 더 자주 접하는 경우가 많고, 코딩테스트의 경우 1개의 테스트 케이스가 아닌 여러개의 테스트 케이스를 모두 통과해야만 합격하기 때문에 최악일 때를 염두해 두어야 합니다.
📍 빅 오(Big - O) 표기법이란?
Big-O 표기법은 알고리즘이 해당 차수이거나 그보다 낮은 차수의 시간복잡도를 가진다는 의미입니다. 즉, 아무리 최악의 상황이라도, 이정도 성능을 보장한다는 의미입니다.
☛ 빅오 표기법 종류
| 종류 | 의미 | 예제 |
|---|---|---|
| O(1) | 데이터 양과 상관없이 일정한 실행 시간을 가짐 | Stack - Push, Pop |
| O(㏒ N) | 연산이 한 번 실행될 때 마다 데이터의 크기가 절반 감소 | 이진트리 |
| O(N) | 입력값(N)이 증가함에 따라 실행시간도 선형적으로 증가하는 알고리즘 | for 문 |
| O(N ㏒ N) | 입력 데이터가 많아질수록 처리 시간이 로그 배만큼 더 늘어납니다 | 퀵 정렬, 합병 정렬, 힙 정렬 |
| O(N²) | 입력 데이터가 많아질수록 처리시간이 급수적으로 늘어납니다 | 삽입 정렬, 버블 정렬, 선택 정렬, 이중 for 문 |
| O(2ⁿ) | 빅오 표기법 중 가장 느린 시간 복잡도 | 피보나치 수열 |
☛ Big - O 표기법 그래프 및 성능 비교
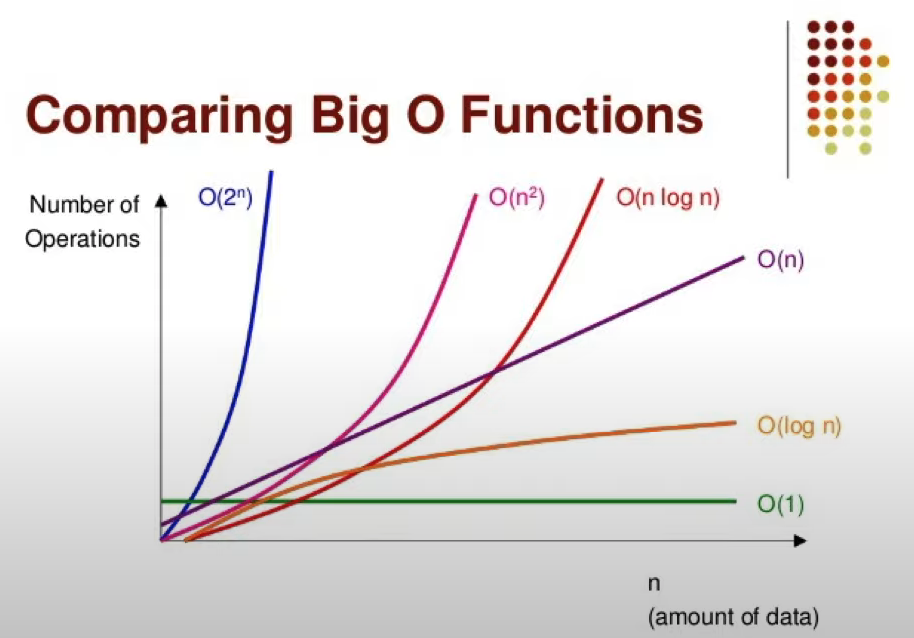
O(1) < O(㏒ N) < O(N) < O(N ㏒ N) < O(N²) < O(2ⁿ)
각각의 시간 복잡도는 데이터 크기의 증가에 따라 수행시간이 다르며 O(2ⁿ)이 가장 효율이 떨어지는 것을 볼 수 있습니다.
