알고리즘 성능 평가
알고리즘의 성능을 평가하기 위해서는 복잡도(Complexity)를 척도로 사용함.
동일한 기능을 수행하는 알고리즘이 있을 때 복잡도가 낮을수록 좋은 알고리즘임.
시간 복잡도(Time Complexity)
시간 복잡도는 알고리즘이 문제를 해결하는데 걸리는 시간을 의미함.
공간 복잡도(Space Complexity)
공간 복잡도는 알고리즘이 얼마나 많은 공간(메모리)를 차지하는지를 의미함.
현재는 컴퓨팅 성능의 발달로 메모리 공간의 여유가 확보되어 과거에 비해 중요도가 떨어짐.
빅오(Big-O) 표기법
점근 표기법의 일종으로 알고리즘의 효율성을 표기해주는 표기범.
점근 표기법의 종류로는 빅오(Big-O), 빅오메가(big-Ω), 빅세타(big-Θ) 표기법이 있음.
빅오 표기법을 사용하는 이유
알고리즘의 효율성을 고려할때는 최악의 경우를 고려해야함.
알고리즘의 효율성은 값이 클수록 비효율적임을 의미하는데, 빅오 표기법은 이를 상한선 기준으로 표기함.
빅오메가는 하한선, 빅세타는 상한선과 하한선의 사이를 기준으로 표기함.
빅오 표기법은 상한선만 지정헀을 뿐, 상한선이 꼭 알고리즘 효율성의 최악의 경우는 아님.
빅오 표기법의 특징
상수항 무시
빅오 표기법은 데이터의 입력값(n)이 충분히 크다고 가정하고 있고, 알고리즘의 효율성 또한 데이터의 입력값(n)의 크기에 따라 영향 받기 때문에 상수항 같은 사소한 부분은 무시한다.
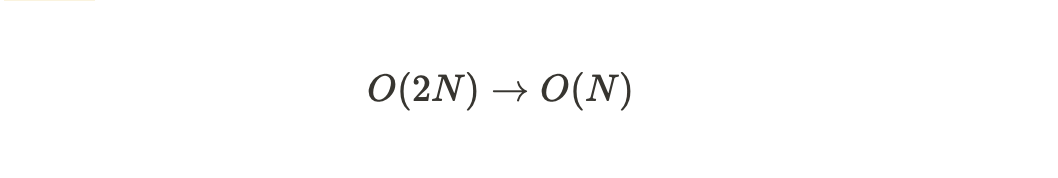
영향력 없는 항 무시
빅오 표기법은 데이터 입력값(n)의 크기에 따라 영향을 받기 때문에 가장 영향력이 있는 큰 항 이외에 영향력이 없는 항들은 무시한다.
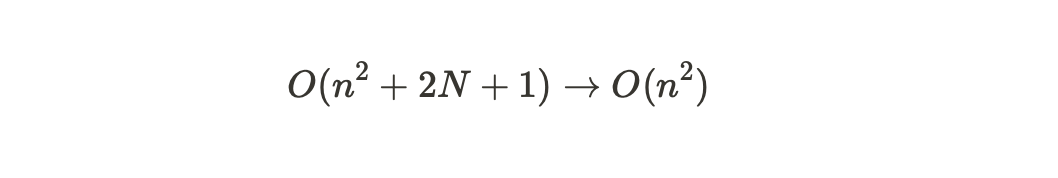
빅오 표기법 성능 비교
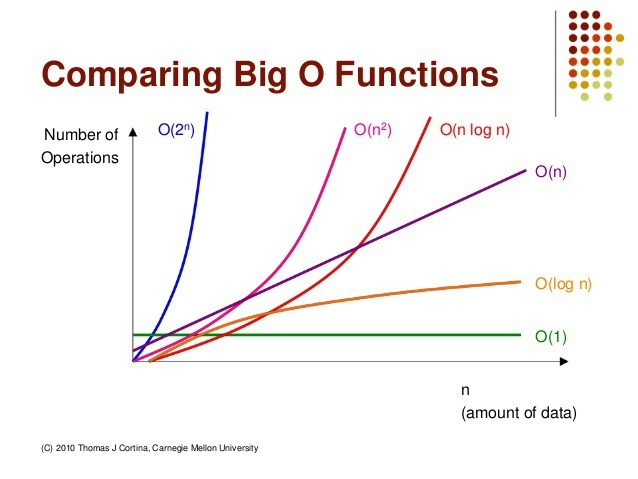
O(1) (상수 시간) : 입력 데이터의 크기에 상관없이 언제나 일정한 시간이 걸리는 알고리즘을 나타냄. 데이터가 얼마나 증가하든 성능에 영향을 거의 미치지 않음.
O(log n) (로그 시간) : 입력 데이터의 크기가 커질수록 처리 시간이 log만큼 짧아지는 알고리즘을 나타냄.
O(n) (직선적 시간) : 입력 데이터의 크기에 비례해 처리 시간이 증가하는 알고리즘을 나타냄.
O(n log n)(선형 로그형 시간) : 데이터가 많아질수록 처리시간이 log배 만큼 더 늘어나는 알고리즘을 나타냄.
O(n²) (2차 시간) : 데이터가 많아질수록 처리시간이 급수적으로 늘어나는 알고리즘을 나타냄.
O(2ⁿ) (지수 시간) : 데이터량이 많아질수록 처리 시간이 기하급수적으로 늘어나는 알고리즘입니다.
시간 복잡도 계산
O(1)
console.log("Hello, World!");O(N)
for(let i = 0; i < n; i++) {
console.log("Hello, World!");
}for(let i = 0; i < n; i++) {
console.log("Hello, World!");
}
for(let i = 0; i < n; i++) {
console.log("Hello, World!");
}
//시간복잡도 계산에는 가장 큰 영향을 미치는 알고리즘 하나만 계산함. O(n²)
for(let i = 0; i < n; i++) {
for(let j = 0; j < n; j++) {
console.log("Hello, World!");
}
}for(let i = 0; i < n; i++) {
for(let j = i; j < n; j++) {
console.log("Hello, World!");
}
}
//내부 for문의 변수 j값이 i이므로 이중 for문보다 시간이 적게 걸림.
//하지만 시간복잡도 계산은 정확한 값을 산출하는 것이 아님.
//근사치를 계산하기 때문에 시간 복잡도가 O(n²)이 됨. 시간복잡도 줄이는 법
- 반복문의 숫자 줄이기
- 적절한 자료구조 이용하기
- 적절한 알고리즘 이용하기
공간 복잡도를 결정하는 것
- 배열의 크기
- 동적할당이 이뤄지는 횟수
- 재귀함수가 호출되는 횟수
프로그램에 필요한 공간은 고정 공간과 가변 공간으로 크게 두가지로 나눠짐.
고정 공간에는 코드, 변수, 배열, 상수들이 해당되고, 가변 공간에는 함수 호출시 할당되는 지역변수, 동적으로 할당되는 객체들이 해당됨.
공간 복잡도 계산
O(1)
let a = 10;
//공간이 하나씩 생성되는 것을 1이라고 표현함.O(N)
function factorial(n) {
if(n === 1) return 1;
return n * factorial(n - 1);
}
//재귀 함수에서는 n값에 따라 공간복잡도가 달라짐.
//n값에 따라 함수가 재귀적으로 호출되기 떄문임. 공간복잡도 줄이는법
- 가변 공간을 사용할 수 있는 자료구조 이용하기
- 재귀적으로 짤 수 있고 반복문으로도 짤 수 있다면 반복문 사용하기
하지만 시간과 공간은 반비례적 경향이 있고, 최근에는 시간 복잡도가 우선시되므로 알고리즘은 시간 복잡도를 중심으로 해결함.
빅오 표기법 예제
- O(1) : 스택에서 Push, Pop
- O(log n) : 이진탐색, 이진트리
- O(n) : for 문
- O(n log n) : 퀵 정렬(quick sort), 병합정렬(merge sort), 힙 정렬(heap Sort)
- O(n²): 이중 for 문, 삽입정렬(insertion sort), 거품정렬(bubble sort), 선택정렬(selection sort)
- O(2ⁿ) : 피보나치 수
