탐욕 알고리즘
탐욕 알고리즘이란 Greedy(탐욕스러운, 욕심 많은) 이라는 뜻을 가진, 그대로 선택의 순간마다 당장 눈앞에 보이는 최적의 상황만을 쫓아 최종적인 해답에 도달하는 방법을 뜻한다.
순간마다 하는 선택은 그 순간에 대해 지역적으로는 최적이지만, 그 선택들을 계속 수집하여 최종적인 해답을 만들었다고해서 그것이 최적이라는 보장은 없다.
하지만, 탐욕 알고리즘을 적용할 수 있는 문제들은 지역적으로 최적이면서 전역적으로 최적인 문제들이라고 한다.
1. 활동 선택 문제
먼저 활동 선택 문제가 그것인데 쉽게 말하면 한 강의실에서 여러 개의 수업을 하려고 할 때 한 번에 가장 많은 수업을 할 수 있는 경우를 고르는 것이다.
아래 표의 s(i)는 시작 시간, f(i)는 종료 시간이다. 같은 강의실을 사용해야 하므로 a(1)과 a(4)는 동시에 선택할 수 없다. a(1)과 a(2)도 시간이 겹치므로 선택할 수 없다. 하지만, a(1)과 a(3)은 선택할 수 있다. 이런 식으로 가장 많은 수업을 들을 수 있는 경우를 찾으면 된다.
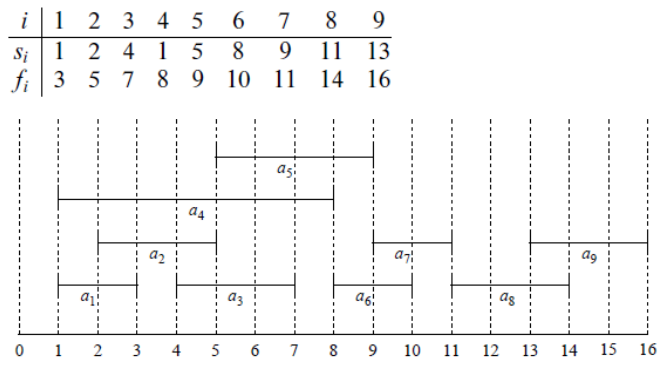
정돈 된 위 그림으로 봤을 때 {a(1), a(3), a(6), a(8)} 이나 {a(1), a(3), a(7), a(9)}를 고르면 된다.
만약 G(1,8)을 a(1)이 종료된 이후부터 a(8)이 시작하기 전 까지의 활동들의 집합이라고 정의해보자.
그렇다면 이 집합은 {a(3), a(5), a(6), a(7)}이 된다.
이 중, 최적의 경우를 B(1,8)이라고 했을 때 (겹치지 않고 최대로 들을 수 있는) 부분집합은 {a(3), a(6)} 또는 {a(3), a(7)}이다.
여기서 {a(3), a(6)} 집합을 계속 탐색해보자. 다음은 이를 쪼개어 G(1,6)과 G(6,8)에서 각각 최적인 B(1,6)과 B(6,8)을 찾는다. 이를 식으로 나타내면 결국 C[i,j] = max(C[i,k] + C[k,j] + 1) 이 된다. 여기서 C는 집합 G(i,j)의 최적의 개수를 나타낸다. max는 B(1,8)에서 a(6) 말고 다른 것을 골랐을 때의 경우도 모두 생각해 그 중 최적의 경우를 찾는 것이다.
이를 그리디로 생각해보면, 최적의 해를 구하기 위해서는 "첫 번째 활동"이 최대한 일찍 끝나면 된다.
여기서는 제일 빨리 끝나는 a(1)을 선택하고, a(1)을 골랐다면 a(2) or a(4)를 고르지 않으면 된다. 그 다음으로 일찍 끝나는 것은 a(3) -> a(6) -> a(8)이다.
이를 구현하기 위해서는 일찍 끝나는 순으로 정렬 후 반복문을 통해 집합의 끝나는 시간이 다음 행동의 시작 시간보다 작은 경우 결과 집합에 추가해주면 된다.
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
List<Integer> res = new ArrayList<>();
StringTokenizer st;
int N = Integer.parseInt(br.readLine());
int[][] times = new int[N][3];
for (int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine());
times[i][0] = i;
times[i][1] = Integer.parseInt(st.nextToken());
times[i][2] = Integer.parseInt(st.nextToken());
}
Arrays.sort(times, new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o1[2] - o2[2];
}
});
int last = 0;
for (int i = 0; i < N; i++) {
if (last < times[i][1]) {
res.add(i + 1);
last = times[i][2];
}
}
System.out.println(res.toString());
}
}입력 예제
9
1 3
2 5
8 10
4 7
5 9
9 11
11 14
13 16
1 82. 배낭 문제
배낭 문제는 dp를 이용한 그리디 알고리즘 중 매우 유명한 문제이다. 배낭에 넣을 수 있는 최댓값이 주어지고 한도의 물건을 넣어 가치의 합이 최대가 되도록 고르는 방법을 찾는 것으로 조합 최적화 문제이다.
이 knapsack 문제는 분할 가능한 배낭문제(Fraction Knapsack) 와 분할 불가능한 배낭문제(0/1 Knapsack Problem) 로 나뉘는데 전자는 Greedy 알고리즘을 쓰고, 후자는 dp를 이용한다.
평범한 배낭
(백준 12865 https://www.acmicpc.net/problem/12865)
이 문제는 분할 불가능 배낭문제로 각 물건의 무게(W)와 가치(V)들이 주어진다.
풀이 과정
입력 예제를 통해 배낭의 무게 한도는 7kg 인 것을 알 수 있고, 각 물건의 무게와 가치는 다음과 같다.
| w | v |
|---|---|
| 6 | 13 |
| 4 | 8 |
| 3 | 6 |
| 5 | 12 |
우리는 최적의 결과를 가지는 집합 A를 구하기 위해 A의 최적 부분집합을 구해야한다. 이 경우 부분집합을 구할 수 있는 방법은 두 가지로 나눌 수 있다.
- 집합 A가 n번 째 물건을 포함하고 있지 않다면, A는 n-1개의 물건들 중 최적으로 고른 부분 집합과 같다. (n-1째 까지의 최적해)
- 집합 A가 n번 째 물건을 포함하고 있다면, n-1개의 물건들 중 최적으로 고른 가치의 합에 n번 째 물건 무게를 더한 것과 같다. (이 때, 가방은 n번 째 물건이 들어간 만큼의 여유를 가지고 있어야한다.)
이 두 가지 경우를 점화식으로 나타내면 다음과 같다.
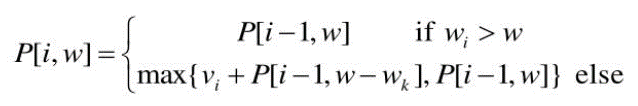
먼저, 물건 무게대로 정렬을 시행한다.
| w | v |
|---|---|
| 3 | 6 |
| 4 | 8 |
| 5 | 12 |
| 6 | 13 |
그 후, 표로 한 번 나타내보자. column은 해당 무게한도를 가진 배낭의 경우이다. row는 i번째 배낭이다.
| i/dp | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 6 | 6 | 6 | 6 | 6 |
| 2 | ||||||||
| 3 | ||||||||
| 4 |
먼저, 배낭의 무게 한도가 0 ~ 2일 때는 첫 번째 물건을 담을 수 없으므로 모두 0으로 setting한다.
그리고 무게한도가 3일 때 부터는 첫 번째 물건을 담을 수 있으므로 쭉 첫 번째 물건의 가치를 넣어준다.
| i/dp | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 6 | 6 | 6 | 6 | 6 |
| 2 | 0 | 0 | 0 | 6 | 8 | 8 | 8 | 14 |
| 3 | ||||||||
| 4 |
2번 째 물건의 경우 배낭의 무게가 3일 때 2번째 물건을 담을 수 없기 때문에 n-1의 최적해가 그대로 내려온다.
그리고 배낭의 한도 무게가 4일 때는 a. 2번 째 물건이 포함되지 않은경우(n-1 최적해)와 b. 2번 째 물건이 포함된 경우인 (2번째 물건의 가치 + 2번째 물건이 포함되지 않은 경우의 무게한도를 가진 배낭의 n-1 최적해) 중 최댓값을 구하면 된다. (점화식 두 번째의 경우를 잘 생각해보자)
이 부분이 이해하기가 가장 어려웠는데 https://www.youtube.com/watch?v=rhda6lR5kyQ&t=601 이 강의를 들어보니 확실히 이해가 갔다.
a의 경우 값은 6이 될 것이고, b는 8 + {(4-4) = 0kg의 무게한도 n-1 최적해} = 0 이 될 것이므로 (1,4) 부분에는 8이 들어갈 것이다.
다음도 마찬가지다.
col5) 6 vs {(5-4)kg의 n-1 최적해 = 0} + 8 ==> 8
col6) 6 vs {(6-4)kg의 n-1 최적해 = 0} + 8 ==> 8
col7) 6 vs {(7-4)kg의 n-1 최적해 = 6} + 8 ==> 14
가 된다.
| i/dp | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 6 | 6 | 6 | 6 | 6 |
| 2 | 0 | 0 | 0 | 6 | 8 | 8 | 8 | 14 |
| 3 | 0 | 0 | 0 | 6 | 8 | 12 | 12 | 14 |
| 4 |
col5) 8 vs {(5-5)kg의 n-1 최적해 = 0} + 12 = 12
col6) 8 vs {(6-5)kg의 n-1 최적해 = 0} + 12 = 12
col7) 14 vs {(7-5)kg의 n-1 최적해 = 0} + 12 = 14
| i/dp | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 6 | 6 | 6 | 6 | 6 |
| 2 | 0 | 0 | 0 | 6 | 8 | 8 | 8 | 14 |
| 3 | 0 | 0 | 0 | 6 | 8 | 12 | 12 | 14 |
| 4 | 0 | 0 | 0 | 6 | 8 | 12 | 13 | 14 |
col6) 12 vs {(6-6)kg의 n-1 최적해 = 0} + 13 = 13
col7) 14 vs {(7-1)kg의 n-1 최적해 = 0} + 13 = 14
우리는 최종 무게한도 7일 때의 최대 가치를 구해야하기 때문에 행렬의 맨 마지막 값을 구하면 된다.
이를 코드로 나타내면 어떻게 될까?
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N, K;
N = Integer.parseInt(st.nextToken());
K = Integer.parseInt(st.nextToken());
int[] W = new int[N + 1];
int[] V = new int[N + 1];
int[][] dp = new int[N + 1][K + 1];
for (int i = 1; i <= N; i++) {
st = new StringTokenizer(br.readLine());
W[i] = Integer.parseInt(st.nextToken());
V[i] = Integer.parseInt(st.nextToken());
}
for(int i = 1; i <= N; i++) {
for(int j = 1; j <= K; j++) {
if (W[i] > j) // 현재 물건의 무게가 배낭의 크기보다 크다면 --> 현재 물건은 포함되어있지 않다는 것이기 때문에 n-1의 최적해를 대입
dp[i][j] = dp[i-1][j];
else
dp[i][j] = Math.max(dp[i-1][j], V[i] + dp[i - 1][j - W[i]]);
}
}
System.out.println(dp[N][K]);
}
}분할 가능한 배낭문제
다음은 분할이 가능한 배낭 문제이다. 이 경우에는 물건이 배낭 무게를 초과할 것 같으면 물건을 쪼개서 넣을 수 있다.
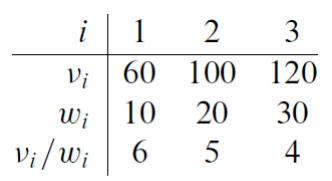
다음과 같은 물건들과 무게 제한은 50이라고 생각해보자. 이 경우 물건을 넣을 때 무게 대비 가치가 높은 것들을 먼저 넣는 것이 좋을 것이다.
- 무게 대비 가치 순으로 정렬 후
- 물건 무게가 제한 이하일 경우 넣고, 물건 무게가 제한 초과일 경우 잘라서 넣는다.
import java.util.Arrays;
import java.util.Comparator;
public class Main {
public static void main(String[] args) {
int[][] item = {{1,60,10}, {2,100,20}, {3,120,30}};
int limit = 50; //배낭의 제한 무게
// 무게 대비 가치 순으로 정렬
Arrays.sort(item, new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
int prev = o1[1]/o1[2];
int cur = o2[1]/o2[2];
if (cur - prev> 0) {
return 1;
}else{
return -1;
}
}
});
int res = 0;
for (int i = 0;i < item.length; i++) {
if(limit > 0) {
if (limit > item[i][2]) {
limit -= item[i][2];
res += item[i][1];
}else {
res += (item[i][1]/item[i][2] * limit);
limit = 0;
}
}else {
break;
}
}
System.out.println(res);
}
}
출처
https://www.zerocho.com/category/Algorithm/post/584ba5c9580277001862f188
https://coding6467.tistory.com/22
