TIL_20240319

오늘 클러스터링 2강 시간이 있었다.

어제 못다한 실습만 진행하는데도 1시간이 지나가버렸다.

유클리디안 거리와 맨하튼 거리, 코사인 거리, 자카드 거리를 배웠다.

# 파이썬 기억할 것
제곱 : ** 2
루트 : ** 0.5

1. 유클리디안 거리 : 점과 점 사이의 직선 거리를 측정하는 것으로 그 거리가 짧을 수록 유사하다고 볼 수 있다. 피타고라스 공식과 다르지 않았다. 수평 수직의 차를 제곱해서 합하는 공식이다.

# 유클리디안 거리 원리
def euclidean_dist(x1, x2):
	dist = 0
  	for a, b in zip(x1, x2):
    	dist += (a-b) ** 2
  	dist = dist ** 0.5
  	return dist

---

2. 맨하튼 거리 : 뉴욕 맨하튼이 격자식으로 되어 있다고 해서 지어진 이름인데, 이 경우는 유클리디안 거리처럼 직선으로 갈 수 없다.격자식으로 계산하기 때문에 수평 수직의 거리를 합하여 계산한다고 한다.

# 맨하튼 거리 원리
def manhattan_dist(x1, x2):
	dist = 0
	for x, y in zip(x1, x2):
    	dist += abs(x - y)
    return dist

---

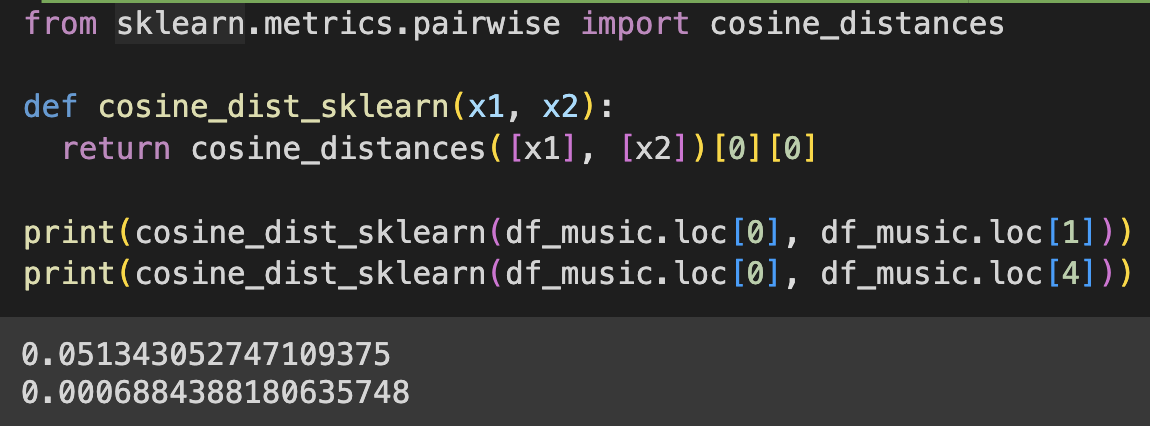
3. 코사인 거리 : 점과 점 사이를 0으로 부터 직선을 그었을 때 나오는 각을 이야기하는 것 같았다. 코사인은 세타라는 기호로 표현하고 코사인 거리를 구하기 위해선 코사인 유사도를 먼저 알아야 했다. 점과 점 사이의 각도가 코사인 유사도인데, 두 점의 거리가 멀수록 유사하지 않고, 각도 또한 커지게 된다. 여기서 구한 그 각(코사인 유사도)을 1에서 마이너스 해준 값이 코사인 거리가 된다.
   * 라이브러리 활용버전

---

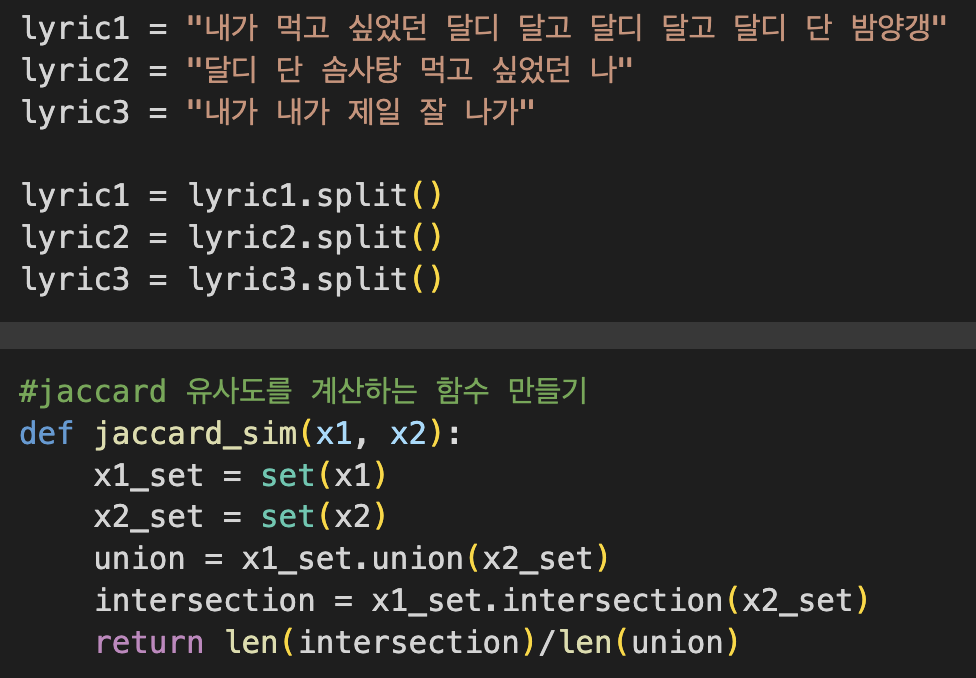
4. 자카드 거리 : 텍스트 분석을 위해 자주 사용되는 방식이라고 한다. 모든 단어를 쪼개고 단어들의 합집합으로 비교하고 싶은 두 대상(리스트나 array)의 교집합을 나누는 것이다. 전체가 구분된 텍스트 중에 얼마나 유사한 텍스트가 많은지를 확인하는 작업이다.
   1~0까지로 표현되며 1에 가까울 수록 유사하다.
   
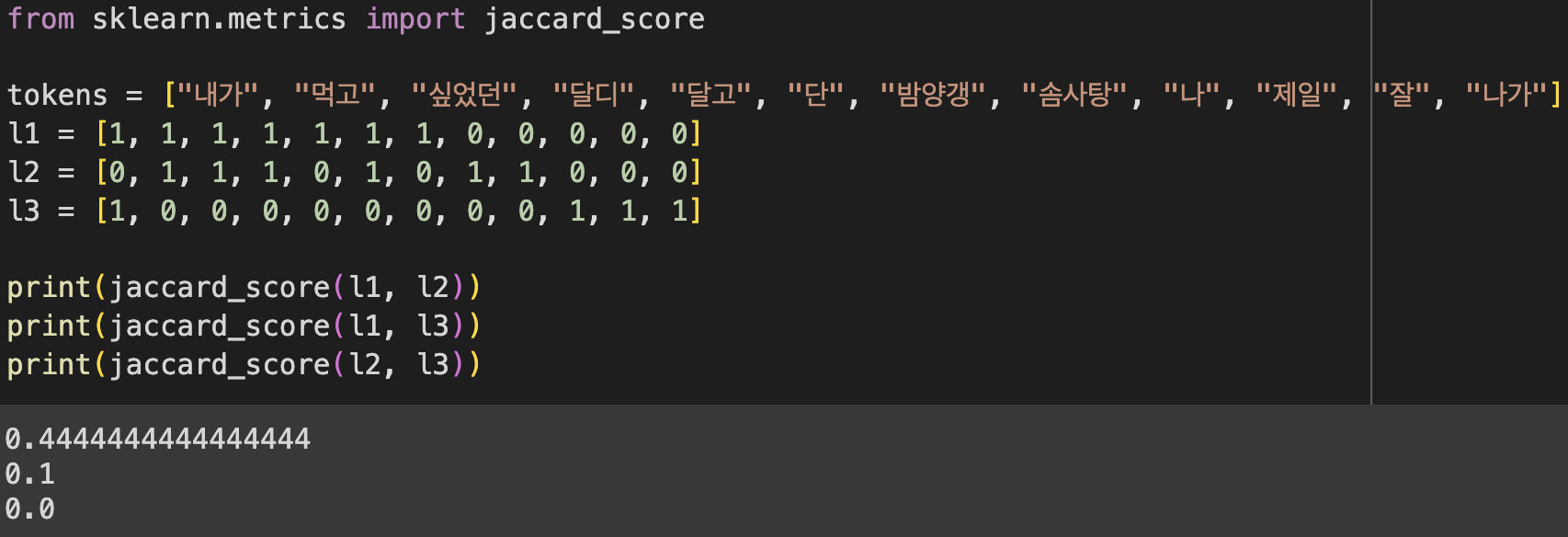
   * 라이브러리 활용버전

이미지는 스파르타코딩 내일배움캠프 과정 중의 내용 일부입니다.