문제

행렬을 범위 단위로 변경하고 각 값을 구해보는 문제다.

행렬이 10^3x10^3 이고
범위 변경(쿼리)가 2.5x10^5 이므로
단순히 행렬을 돌며 값을 변경하면 10^11로 시간초과다.

그래서 변경을 중복적으로 진행해서는 안된다.

누적합

내가 아는 부분 구간의 합인 세그먼트 트리를 이용해 먼저 구현해봤는데 구간의 합을 물어보는게 아니었기에 빅오는 그대로였다.

부분적으로 더하고 빼면 될거같았는데
막상 마주하니 생각할수 없어 부분합을 검색했다.
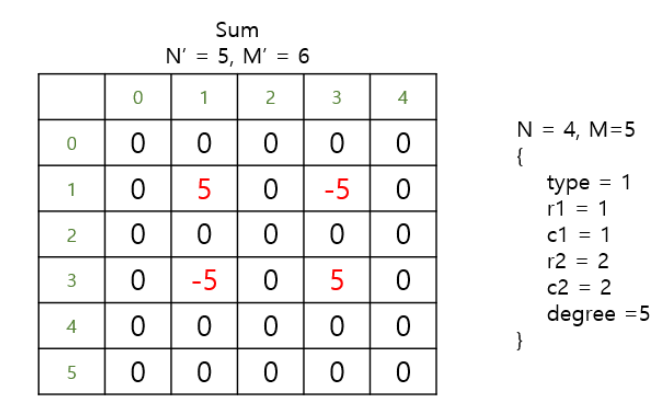출처 https://jangcenter.tistory.com/121

딱 저 그림을 보니까 어떻게 표현할지 감이왔다.

Code

package kakako2022;
class Solution6 {
    // skill
    // 1-공격, 2-회복
    // [type, r1, c1, r2, c2, degree]
    // board 10^3,10^3 10^6
    // skill 2.5*10^5=2^18
    private static int n,m;
    private static int[][] graph;
    public int solution(int[][] board, int[][] skill) {
        // init
        n=board.length;m=board[0].length;
        graph=new int[n+2][m+2];
        for(int[] s:skill){
            int type=s[0],r1=s[1]+1,c1=s[2]+1,r2=s[3]+1,c2=s[4]+1,degree=type==1?-s[5]:s[5];
            // 1,2 3,4
            graph[r1][c1]+=degree;
            graph[r2+1][c1]-=degree;
            graph[r1][c2+1]-=degree;
            graph[r2+1][c2+1]+=degree;
        }
        // sum
        for(int i=1;i<=n;i++){
            for(int j=1;j<=m;j++){
                graph[i][j]+=(graph[i-1][j]+graph[i][j-1]-graph[i-1][j-1]);
            }
        }
        // check
        int ans = 0;
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                if(board[i][j]+graph[i+1][j+1]>=1) ans++;
            }
        }
        return ans;
    }
}
public class P6 {
    public static void main(String[] args) {
        Solution6 sol=new Solution6();
        int[][] board={{5,5,5,5,5},{5,5,5,5,5},{5,5,5,5,5},{5,5,5,5,5}};
        int[][] skill={{1,0,0,3,4,4},{1,2,0,2,3,2},{2,1,0,3,1,2},{1,0,1,3,3,1}};
        System.out.println(sol.solution(board,skill));
    }
}