Graph Representation Learning

sheep·2021년 6월 20일

GNN

목록 보기

1/6

representation learing?
- 어떤 task 를 수행할 수 있는 표현을 만드는 것
- 임베딩이 필요한 이유는 Adjacency Matrix 가 매우 sparse 하기 때문에 computation 측면에서 필요
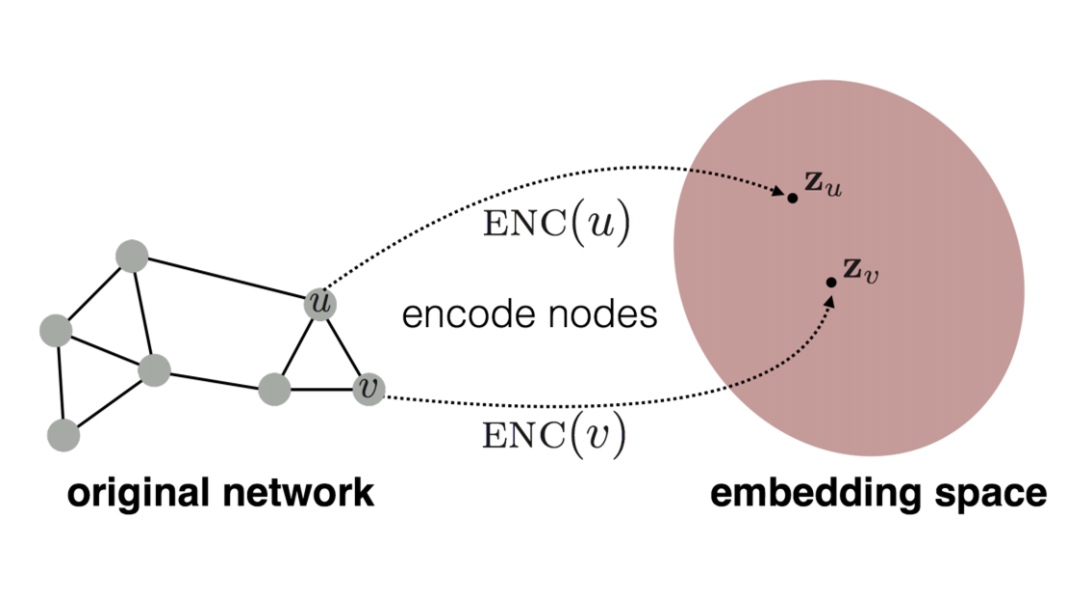
- 임베딩의 목적은 원본 Graph 의 유사도와 embedding space에서 유사도를 최대한 유사하도록 학습하는 것
임베딩 과정

1) Define Encoder

2) Define node similarity function

3) Similarity(u, v) 최적화

node위를 랜덤하게 걷는 것(random sequence path를 만드는 것)
$z_u^t z_v$ : 네트워크 전체의 Random walk 에서 u와 v가 함께 발생할 확률

1) node u에서 출발해 v에 방문할 확률 $P_R(v|u)$ 을 구함(근사 추정)

2) $P_R(v|u)$ 을 인코딩하기 위한 임베딩 최적화
학습과정
- node의 neighborhood를 예측하는 방향으로 feature representation을 학습하겠다.
  
  1) graph의 각 node에서 정해진 길이만큼 random walk 수행
  
  2) 각 노드의 neighborhood $N_R(u)$ 를 수집
  
  3) node u가 주어질 때, 그 node의 $N_R(u)$ 을 잘 예측하는 방향으로 노드 임베딩 수행
  
  → $max_z \sum_{u \in N_R(u)}logP(N_R(u)|z_u)$
Loss Function

$L = \sum_{u\in v}\sum_{v\in N_R(u)} -log(P(v|z_u))$

→ random walk 가 동시 발생할 likelihood를 maximize하는 방향으로 학습

동시에 발생할 likelihood → ${exp(z_u^tz_u)} \over \sum{_n {exp(z_u^tz_n)}}$

→ 의미를 해석해보면 기준 노드 u와 아무 노드 n의 유사도 합 → 분모(작을수록 good)

→ 기준 노드 u와 아무 노드 v의 유사도 합 → 분자(높을수록 good)

→ 이 확률이 높아질수록 Loss가 낮아짐

→ node의 이웃을 잘 예측하고 있음

단점
두 노드의 structural role이 비슷하지만 멀리 떨어져 있는 경우, random walk는 fixed size조건으로 neighborhood node를 탐색하기 때문에 한계가 있음 → graph structure 정보를 활용하기 위해 node2vec제안

random walk 를 일반화하여 탐색하는 알고리즘
네트워크 상에서 이웃놀드를 찾아내는 방법을 유연하게 정의해서 그래프 임베딩을 하겠다.
global/local 구조 어디에 더 집중할 지, 2nd-order 랜덤 워크 사용
- 1st-order random walk : node-node transition
- 2nd-order random walk : edge-edge transition
그래프의 이웃을 찾는 두 방법
- BFS : local 구조 중심
- DFS : global 구조 중심
두 파라미터 조정
- p : 이전노드로 돌아온 정도
- q : BFS와 DFS의 비율
알고리즘 과정

1) 랜덤 워크 확률 구하기

2) 각 노드에서 시작하는 길이 i의 랜덤워크를 r번 시행

3) SGD를 통해 최적화
임베딩된 노드 당 $z_i$ 의 벡터를 아래 sub task에 활용
- 클러스터링/커뮤니티 탐지 : $z_i$ 에 대해 클러스터링 적용
- 노드 분류 : $z_i$ 를 바탕으로 $f(z_i)$ 의 target을 예측
- 링크 예측 : $f(z_i, z_j)$ 를 바탕으로 (i, j)가 존재하는지 여부 예측, $f$ : 임베딩 결과에 평균, 곱, 거리 등의 다양한 연산 적용한 결과
노드간 유사도를 구하는 방법

1) Adjacency 기반

2) Multi-hop 유사도

3) 랜덤워크 기반(node2vec)

해결하고자 하는 문제에 적합한 방식 선택하기
- 노드 분류 문제 : node2vec
- 링크예측 : multi-hop 유사도

Q. 그래프 전체를 임베딩 시키는 법?

인코더 정의(네트워크 ↔ 임베딩 맵핑하는 함수)
- 노드별 임베딩 결과를 담고 있는 행렬 Z를 학습하고, 특정 노드가 주어지면 Z에서 해당 노드의 임베딩 값을 가져오자(embedding lookup)
- 임베딩 행렬 Z는 (노드 개수 X 임베딩 차원수) 행렬
노드 간 유사도 함수를 정의
- 예를들어, 얼마나 직접 연결되었는지?, 얼마나 동일한 이웃을 가졌는지?, 네트워크 구조상 비슷한 역할인지?, etc...
원본 네트워크 상에서의 유사도와 임베딩 공간에서의 유사도가 비슷해지도록 모델 파라미터 학습

→ 임베딩 노드간의 $(z_uz_v)$ 사이 관계가 원본 네트워크 (u, v) 의 유사도를 가장 잘 표현하는 encoder를 찾자.

출처