구간의 합

✏️ 구간 합 이란

• 구간 합은 합 배열을 이용해 시간 복잡도를 더 줄이기 위해 사용하는 특수한 목적의 알고리즘 이다.
• 배열의 특정 구간만의 값을 빠르게 구할 때 사용하는 기술이다.
  • 코딩 테스트에서 사용 빈도가 높은 기술이다.

✏️ 합배열

📍 합배열 개념

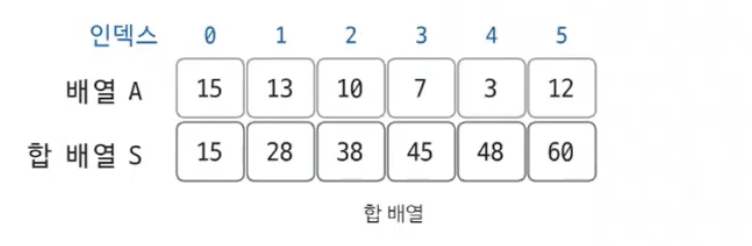
• 합배열은 기존 배열을 전처리한 배열이다.
• 합배열은 기존 배열의 0번 인덱스부터 i 번째 인덱스를 모두 더한 값을 뜻한다.
  • 보통 S[i] 이런식으로 표기한다.

S[i] = A[0] + A[1] + A[2] + ... + A[i -1] + A[i]

• 합배열 예시

📍 합배열 만드는 방법

• 합배열을 만드는 공식
  • 공식을 봤듯이 합배열은 순서대로 만들지 않으면 만들 수 없다.
  • 0번 인덱스 값은 별도로 지정해줘야 한다.

S[i] = S[i - 1] + A[i]

📍 구간합을 구하는 방법

• 합배열을 응용해 0번째 인덱스 부터의 합을 구하는 것이 아닌, 특정 인덱스 부터 합을 구하는 방법이다.
• 합배열을 이미 구했을 경우 구간합은 아주 빠르게 구하는 공식이 있다.
  • 아래 공식은 i 번 인덱스 ~ j 번 인덱스 까지의 구간 합을 구하는 공식이다.

S[j] - S[i - 1]

• 이미 합배열이 준비되어있다면 간단한 공식으로 구간합을 구할 수 있다.

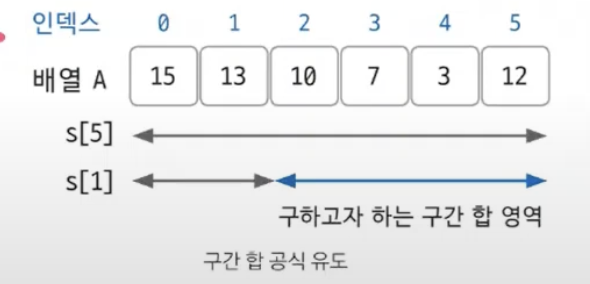
• 아래 예제에서 2번 인덱스 ~ 5번 인덱스 까지 의 구간합을 구하려면 아래의 공식을 사용하면 된다.
  • 공식의 원리는 간단하다.
    구간이 끝나는 합배열의 인덱스에서 구간이 시작되는 합배열의 인덱스를 빼줌으로써 구간의 합을 효율적으로 구할 수 있다.

구간합 = S[5] - S[1]

⚠️ 합배열의 한계

• 합배열은 원본 배열의 인덱스가 변하지 않는다면 얼마든지 빠른 구간합을 구할 수 있지만,
  인덱스 값이 변하게 되면 사용할 수 없게된다.
• 이러한 단점을 보완하기 위해 세그먼트 트리 라는 기술이 존재한다.