롤케이크 자르기

INPUT

롤케이크 위에 올려져 있는 토핑의 종류를 담고 있는 배열

OUTPUT

롤케이크를 공평하게 자르는 방법의 수

CONSTRAINTS

1 ≤ topping의 길이 ≤ 1,000,000
1 ≤ topping의 원소 ≤ 10,000

Input으로 들어온 배열인 topping을 자른다.
[1, 2, 1, 3, 1, 4, 1, 2] 형태로 들어온 케이크가 있으면, 0번과 1번 사이를 기준으로 자르게 되면
[1], [2, 1, 3, 1, 4, 1, 2] 형태로 잘리게 된다.
이때 왼쪽(철수) 는 토핑이 1종류 (1) 이다.
오른쪽(동생) 은 토핑이 4종류 (1,2,3,4) 이다
케이크의 크기와 무관하게 둘의 토핑의 종류가 같으면 공평하게 자른 것이다.

LOGIC

1. 완전 탐색

Set 을 이용해서 했다.

public static int solution(int[] topping){
        // 처음에 young 에 모두 추가
        // i번째 껄 old 에 추가
        // i번째 토핑이 i번째 이후에 등장하면 그대로 두고
        // 등장하지 않으면 young 에서 해당 토핑도 빼줌
        Set<Integer> old = new HashSet<>();
        Set<Integer> young = new HashSet<>();
        for(int top : topping){
            young.add(top);
        }

        int youngSize=young.size();
        int oldSize=0;
        int count=0;

        // i 번째 토핑을 왼쪽에 더하고 오른쪽에선 뺌
        for(int i=0;i<topping.length;i++){
            //System.out.println(old+" "+ young);
            int top = topping[i];
            if(old.add(top)){
                oldSize+=1;
            }
            boolean flag = false;
            for(int j=i+1;j<topping.length;j++){
                if(topping[j]==top){
                    flag=true;
                    break;
                }
            }
            if(!flag){
                young.remove(top);
                youngSize-=1;
            }
            if(oldSize==youngSize){
                count++;
            }
        }

        return count;
    }

2. 동적 프로그래밍
   1번으로 직접 풀어보고, 실행 시간이 너무 길어서 풀이를 보았다. 오른쪽(동생)에게 모든 토핑이 있는 상태에서 한개씩 떼어서 주기 때문에 DP 로 풀이가 가능하다.

   우선 토핑의 원소는 최대 1만 이므로 길이 10001 짜리 정수 배열 right , left 를 만든다.
   right[i] 는 동생이 가진 토핑 ' i ' 의 갯수를 나타낸다.
   ex) right[2] = 3 이라면, 2라는 토핑을 3개 가지고 있는 것이다.

1. 우선 모든 토핑을 동생이 가지고 있으니, right 배열을 업데이트한다.

2. 오른쪽(동생) 이 갖고 있는 토핑의 갯수를 업데이트한다. 		   

3. 토핑 배열을 기준으로 시작한다.	
 # 1. 토핑이 i 라 하면, right[i] 를 조회한다.
 ## right[i] 가 0이면, 동생이 해당 토핑을 더 이상 갖고있지 않음
 ### 동생이 갖고있는 토핑 갯수가 하나 줄어든다. 
 
 # 2. 왼쪽(철수) 가 갖고 있는 토핑 정보인 left[i]를 조회
 ## 2-1. left[i]가 0이면 i 토핑을 철수가 갖고있지 않다. 
 ####### 철수가 갖고있는 토핑 종류가 1 증가하고, left[i] 를 1 증가시킨다.
 ## 2-2. left[i] 가 0이 아니면 해당 토핑의 갯수만 1 증가.
 
 # 3. 철수와 동생이 갖고있는 토핑 종류가 같으면 카운트를 증가시킨다.

  public static int solution(int[] topping) {
      int answer = 0;

      // topping 의 원소는 10000 이하 이므로 배열의 길이는 10001
      int[] left = new int[10001];
      int[] right = new int[10001];

      // 왼쪽의 토핑 갯수
      int leftTopping = 0;
      // 오른쪽의 토핑 갯수
      int rightTopping = 0;

      // i 번 토핑이 나타난 횟수
      for(int i : topping){
          right[i]++;
      }

      // 오른쪽에 모든 토핑 있다고 가정
      for(int i : right){
          if(i>0){
              rightTopping+=1;
          }
      }

      // 어차피 왼쪽(철수)에게만 토핑이 추가됨
      // 토핑이 i면, 오른쪽에 있는 토핑 정보에서 i번째 인덱스를 감소시켜줌 (토핑 갯수 하나 줄어듬)
      // 감소시킬 때, right[i] 가 0이면 오른쪽에도 i 토핑이 없는 것. -> right 가 갖고있는 토핑 종류가 하나 줄어듬
      // left[i] 가 0이였으면, left 에 해당 토핑이 없었다는 것임. 따라서 토핑 갯수 1개 늘어남
      // left[i] 에 i 토핑이 1개 추가됨

      // left 토핑 갯수 == right 토핑 갯수 이면 카운트 증가가

      for(int i : topping) {
          right[i]--;
          if (right[i] == 0) {
              rightTopping--;
          }
          if (left[i] == 0) {
              leftTopping++;
          }
          left[i]++;
          if (rightTopping == leftTopping) {
              answer++;
          }
      }
      return answer;
  }

회고

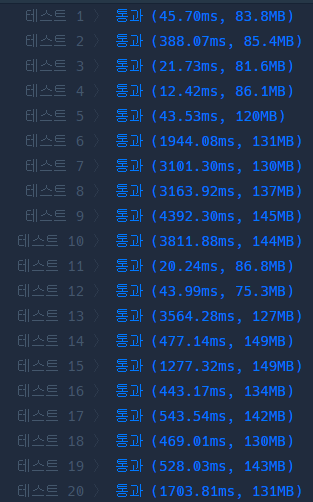
완전 탐색 풀이 실행시간

DP 풀이 실행시간

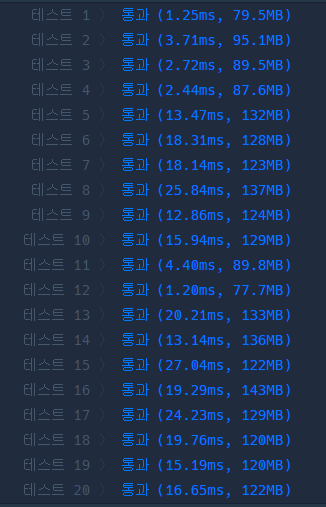
차이가 너무크다. 멍충멍충