[프로그래머스] 후보키

문제링크
https://programmers.co.kr/learn/courses/30/lessons/42890

📂 분류

비트마스크 구현

💡 풀이

column이 최대 8개이기 때문에 조합의 경우의 수는 8!이므로 시간복잡도 걱정없이 모든 조합을 구해 문제를 풀 수 있다.

조합을 구하는 방법은 비트마스크를 이용해 부분집합을 구했다.

아래 예시를 보면 & 연산을 하면 후보 키가 되는 것을 알 수 있는데 이것으로 최소성을 만족하는지 알 수 있다.

// 예시
0001 0      // 유일성o, 최소성o
0010 1      // 유일성x
0011 0 1    // 유일성o, 최소성x
0100 2      // 유일성x
0101 0 2    // 유일성o, 최소성x
0110 1 2    // 유일성o, 최소성o
0111 0 1 2  // 유일성o, 최소성x
...

// 기존 후보 키 k = 0001
// 유일성은 만족 하는 키 i = 0011
k & i == k // 0001 & 0011 == 0001

만약 최소성을 만족했다면, set에 튜플들을 저장한다. 그리고 row의 길이와 set의 크기를 비교해서 같으면 유일성과 최소성이 만족하므로 candiateKey에 추가한다.

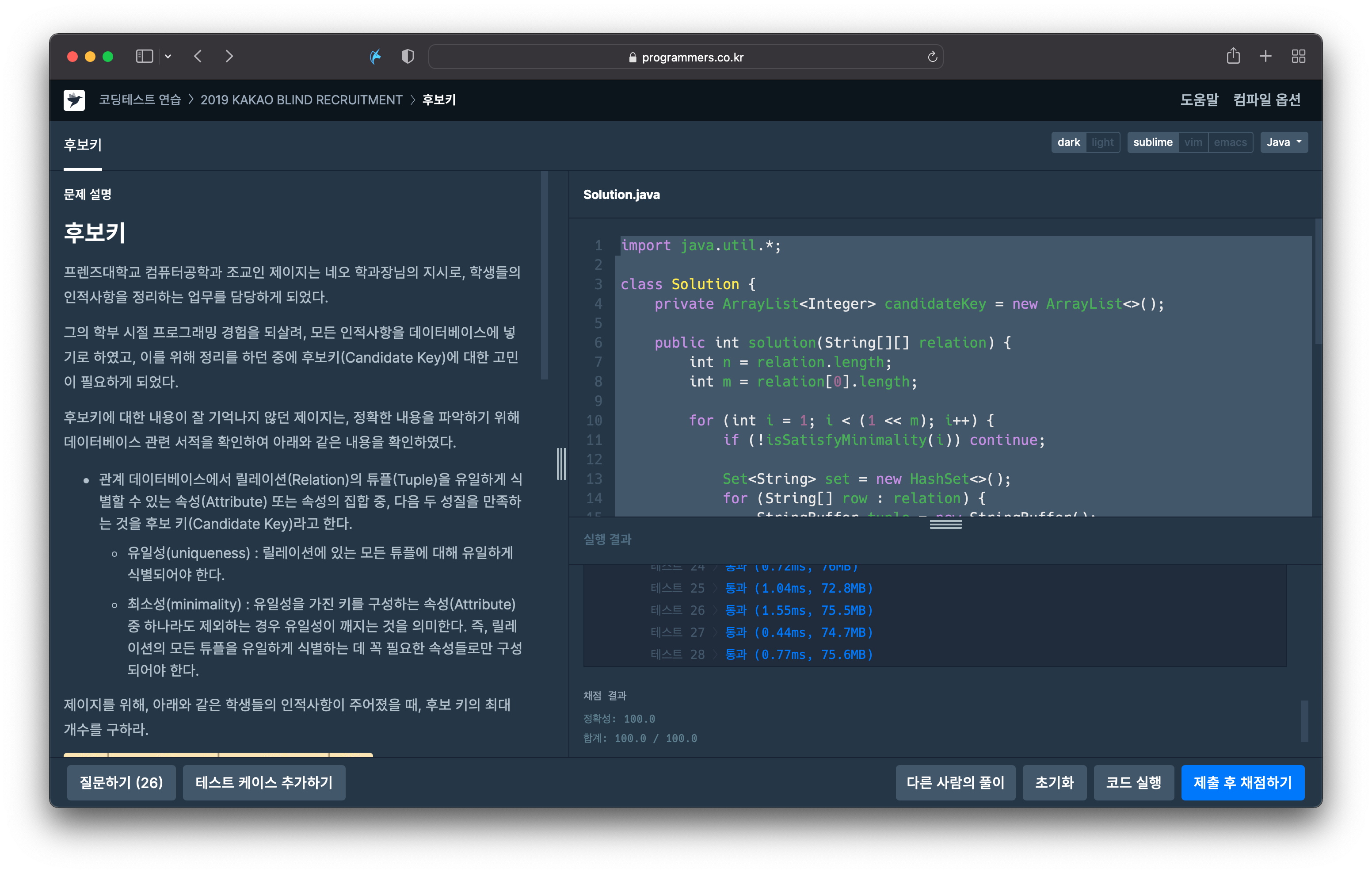
💻 코드

import java.util.*;

class Solution {
    private ArrayList<Integer> candidateKey = new ArrayList<>();

    public int solution(String[][] relation) {
        int n = relation.length;
        int m = relation[0].length;

        for (int i = 1; i < (1 << m); i++) {
            if (!isSatisfyMinimality(i)) continue;

            Set<String> set = new HashSet<>();
            for (String[] tuple : relation) {
                StringBuffer data = new StringBuffer();
                for (int j = 0; j < m; j++) {
                    if ((i & (1 << j)) != 0) {
                        data.append(tuple[j]);
                    }
                }
                set.add(data.toString());
            }
            if (set.size() == n)
                candidateKey.add(i);
        }
        return candidateKey.size();
    }

    private boolean isSatisfyMinimality(int i) {
        for (int key : candidateKey) {
            if ((i & key) == key) return false;
        }
        return true;
    }
}