최장 공통 부분 수열(LCS, Longest COmmon Subsequence)

여러 개의 수열 중에서 모두의 부분수열이 되는 수열들 중, 가장 긴 것을 찾는 문제를 풀어보았습니다.

여러 개의 문자열 중에서, 연속되어 있는 공통문자열을 찾는 문제인 Longest Common Substring과는 다른 문제이니, 혼동하지 않도록 주의해야 합니다.

LCS 알고리즘 개념

str1과 str2의 LCS는 세 가지 값들을 비교해서 결정이 됩니다.

• (1) str1의 마지막 철자를 뺀 부분문자열과 str2의 마지막 철자를 뺀 부분문자열끼리 비교한 LCS값
• (2) str1의 마지막 철자를 뺀 부분문자열과 str2를 비교한 LCS값
• (3) str1과 str2의 마지막 철자를 뺀 부분문자열

(1)은 str1의 마지막 철자와 str2의 마지막 철자가 같은 철자일 때 활용이 됩니다.
그렇지 않다면 (2),(3) 중 더 큰 값이 LCS값이 됩니다.

관련 문제

백준9251-LCS

백준 9251 LCS로 개념 연습하기!

LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다.

예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다.

위 예시로 주어진 두 문자열의 LCS를 구하는 방법을 생각해보도록 하겠습니다. 가장 직관적인 방법부터, 효율적인 방법 순으로 접근해 보도록 하지요.

직관적 풀이

직관적으로 생각하면, 두 문자열의 부분수열을 모두 구해서, 그 중 겹치는 부분수열의 최장길이를 구하면 되겠다는 생각이 먼저 들었습니다.

길이가 n인 부분집합의 수는 2의 n거듭제곱이니, 길이가 6인 문자열의 모든 부분집합의 수는 64개일 것입니다(ACAYKP의 경우).

그럼 64개의 부분집합 묶음이 두 개있으니, 일치하는 부분집합을 구하려면 64 * 64 = 2의 12제곱번의 연산이 추가로 필요하겠네요.

딱 봐도 비효율적인 것 같아요 O(n**2)시간의 작업이 포함되어 있으니까요.

게다가 문제에서는 문장의 길이가 1000이하라고 했으니, 이 방법은 그렇게 좋아보이는 접근법이 아닌 것 같습니다.

효율적인 방법

답을 먼저 말하자면 동적 계획법(Dynamic Programming, 줄여서 DP) 접근법이 효율적입니다.

그렇다면 왜 이 문제에서는 DP를 사용하는 것이 좋을까요?

그 이유는 이 문제가 더 작은 부분문제로 쪼개질 수 있고, 현재 단계의 해답을 찾기 위해서는 필연적으로 과거 시행에 대한 정보를 요구하기 때문 입니다.

위 두 조건을 보면 재귀와도 비슷합니다. 실제로 LCS문제는 점화식을 보면 재귀 형식이에요. 그렇지만 재귀는 겹치는 부분문제(같은 계산을 다른 재귀 트리에서 또 해야 하는)문제가 존재합니다. 그리고 이 문제를 해결하기 위해 이미 해결된 부분문제에 대한 값을 별도의 공간에 저장(메모이제이션)함으로써 시간적인 이득을 보는 것이 DP 접근법이지요.

Top-to-Bottom이 재귀적인 접근법이라면, Bottom-to-Top이 DP라고나 할까요? ㅎㅎㅎ

실전문제를 통한 개념 이해

위 예시 문장 ACAYKP와 CAPCAK의 LCS를 구해보면서, 더 작은 부분문제로 쪼갠다는 것이 어떤 의미인지, 또 겹치는 부분문제란 무엇인지 자세히 알아보죠.

ACAYKP는 앞으로 사용할 그림에서 횡 인덱스에 매핑하도록 할게요. 앞으로 각 철자들은 편의상 인덱스 순서대로 R0, R1, R2...Rn 이렇게 명명하겠습니다.

CAPCAK의 철자들은 인덱스 순서대로 C0, C1, C2, ... Cn으로 명명하겠습니다.

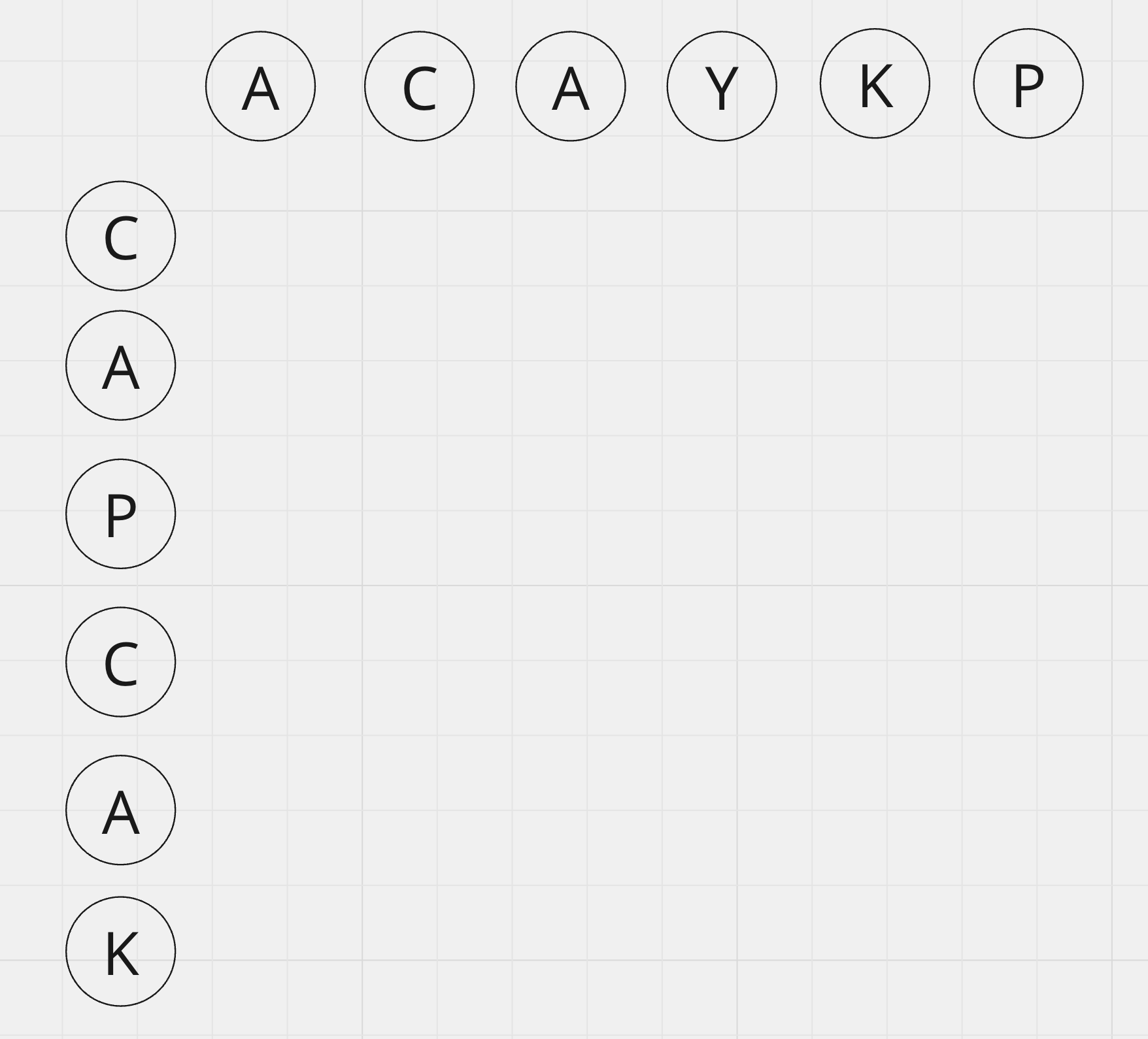
우리는 위 두 문자열의 겹치는 부분수열을 구하기 위해서 철자끼리 비교해야 합니다. 그런데 이 작업은 한 번에 할 수 없어요. 그래서 우리는 생각을 하게 됩니다.

문자를 앞에서부터 하나씩 쌓아가면서 비교하고, 이전 수행에 대한 결과를 기록하는 방법은 어떨까?

부분 문자열들을 비교한 LCS값을 기록하는 2차원 테이블을 dpTable이라 명명하겠습니다.

각 문자열의 첫 철자인 A와 C를 비교해 보기로 합니다.

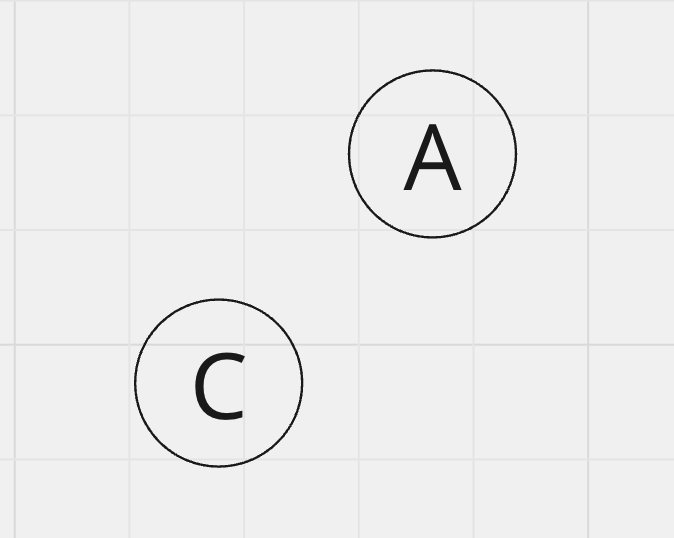
일치하지 않네요. 공통 부분수열은 아직 공집합이니, 0을 기록해줍시다.

메모이제이션 테이블에서 좌표(i,j)에 해당하는 값은 문자열R[0,i]와 문자열C[0,j]를 비교했을 때의 LCS값입니다. 그리고 유효하지 않은 좌표의 LCS값은 0으로 간주해요.

그럼 이번엔 횡의 문자열을 하나 늘려서 R0~R1와 C0를 비교해 보도록 할게요.

'AC'와 'C'는 겹치는 부분이 존재해요. 그래서 이제 LCS길이가 0 +1 = 1이 되었어요!

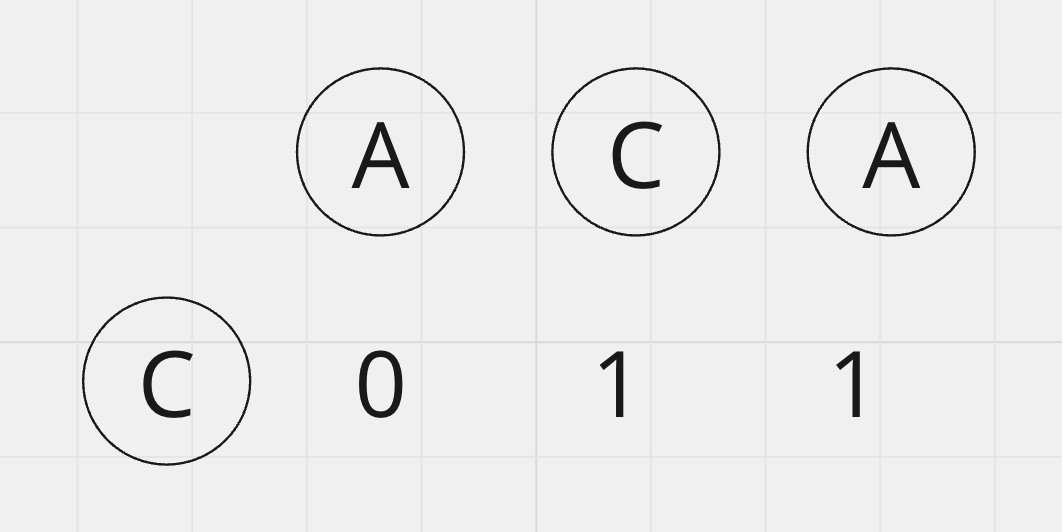
이제 철자를 하나 더 추가해서 'ACA'(R0~R2)와 'C'(C0)를 비교해보도록 하죠. 새로 추가한 A는 우리가 비교로 하는 C와 일치하지 않습니다. 그래서 LCS의 길이는 1로 유지되죠.

이후 Y, K, P에 대해서도 LCS는 1로 유지가 될 것입니다.

그럼 이제 'ACAYKP'와 'C'의 비교가 끝났으니 'CA'와 비교를 할 차례입니다.
'CA'와 비교한 LCS값은 1번 row에 기록이 될 것입니다. 'C'(C0)랑은 비교를 한 결과를 활용해서 'A'(C1)를 추가하여 비교한 결과를 메모이제이션 테이블에 갱신해보도록 하죠. 테이블이 갱신되는 논리가 중요합니다!

'CA'의 두 번째 철자인 'A'(C1)와 'ACAYKP'의 첫 철자인 'A'(R0)가 일치합니다.
우리가 업데이트해야하는 좌표인 (0,1)은 R[0]과, C[0,1]문자열을 비교했을 때의 LCS값입니다.

이 값은 세 가지 종류의

이전 수행인 'C'(C0)와 'ACAYKP'의 'A'(R0)를 비교했을 때는 LCS의 길이가 0이었는데, 이제는 하나 늘어난 1이 되었어요.

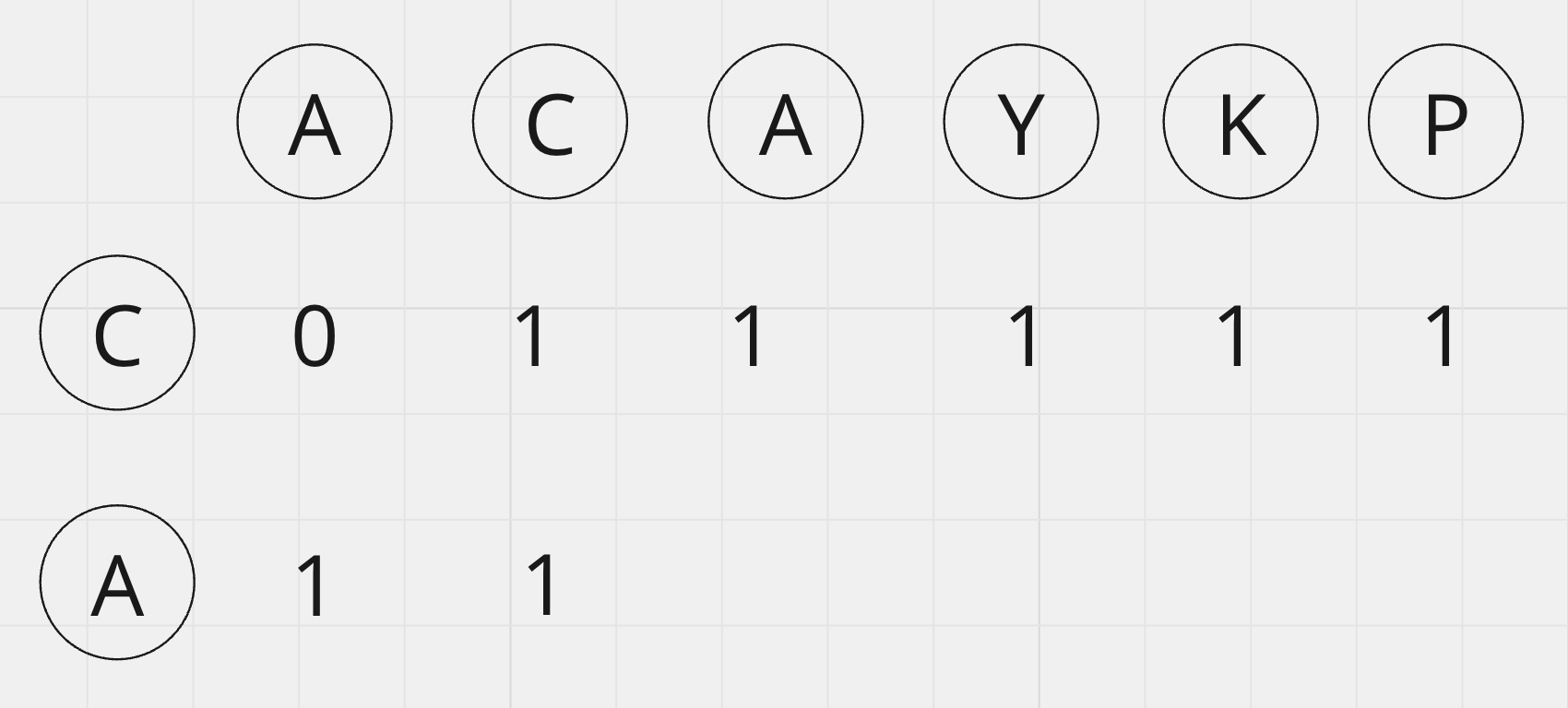
'ACAYKP'(R0~R5)의 R1과 CA(C0~C1)의 C1과 비교할 때는 둘이 일치하지 않습니다. 그래서
dpTable[1][1]을 갱신할 때는 dpTable[0][1]과 dpTable[1][0] 중 더 큰 값으로 갱신해줍니다.

이를 풀어서 설명하자면 'AC'와 'CA'의 LCS값은, 'AC'와 'C'의 LCS값 또는 'A'와 'CA'의 LCS값 중에서 더 큰 값이라는 뜻입니다. 이 경우에는 1로 동일하니 dpTable[1][1]을 1로 갱신해줍니다.

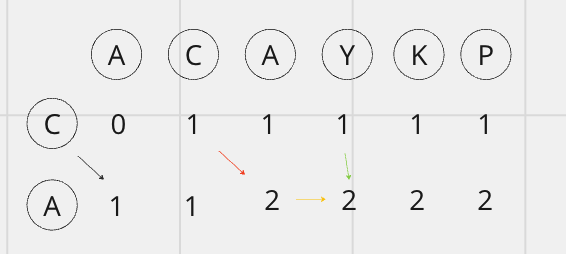
dpTable[1][2]에서는 두 철자가 A로 동일합니다. 이 경우에는 테이블상으로는 대각선 좌측상단인 dpTable[0][1]의 값에서 하나 증가시켜주어야 합니다. 'AC'와 'C'의 LCS는 길이가 1인 'C'문자열이었는데, 맨 끝에 동일하게 'A'가 추가되었으니 LCS가 'CA'로 길이가 길어진 것을 반영한 값입니다.

dpTable[1][3]에서는 Y, A로 두 철자가 다릅니다. 이 경우에는 dpTable[0][3], dpTable[1][2]의 값 중 큰 값인 2로 갱신해줍니다.

이렇게 테이블을 갱신하다보면

요런 테이블이 나오고, 우리가 원하는 답은 마지막 좌표에 있으니 4가 되겠습니다.

더 작은 부분문제로 쪼갤 수 있음

위 테이블을 갱신하면서 우리는 원래 길이의 문자열들을 최대한 작게 만들어놓고 철자를 추가하며 비교를 했습니다. 문자열이 길든 짧든, LCS값을 갱신하는 로직은 동일했으니, 크기만 작은 동일한 문제였음을 알 수 있습니다.

겹치는 부분문제

만약 위의 비교를 재귀를 이용해서 풀어야 했다면, 우리는 수많은 동일한 비교를 수행해야 했을 것입니다.

가령, ACAY와 CA의 비교는 ACA와 CA의 비교, ACAY와 C의 LCS값을 요구하고, 이 비교들은 ACAY와 CAP를 비교할 때도 필요한 연산이 됩니다. 그렇기에 dpTable로 반복된 계산을 캐싱하는 효과를 이뤄내어 시간효율성을 높일 수 있었습니다.

결론

과거의 값이 현재 계산에 영향을 주는 것 같으면 DP 도입을 고려해보자!