[Algorithm] Union-Find(합집합 찾기)

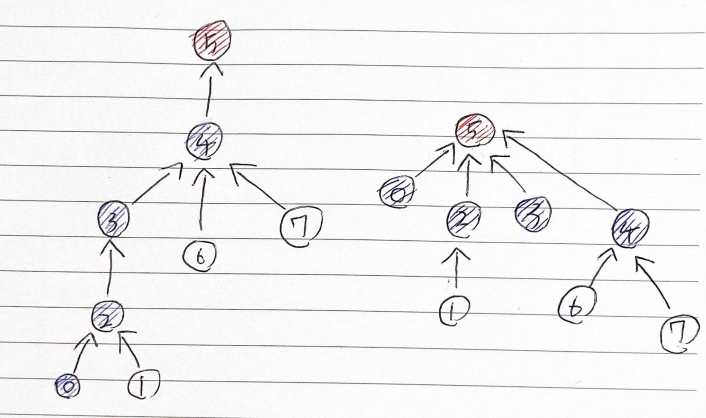
유니온 파인드란?

Union-Find(유니온-파인드는) 대표적인 그래프 알고리즘이다. 쉽게 말해서 '합집합 찾기' 다른 말로는 서로소 집합(Disjoint-Set) 알고리즘이라고도 부른다.

여러 개의 노드가 존재할 때 두 개의 노드를 선택해서, 현재 이 두 노드가 서로 같은 그래프에 속하는지 판별하는 알고리즘. 이후에 고급 알고리즘에도 이 원리가 적용되므로 확실하게 알아두는 것이 좋다. ex) 크루스칼

핵심 연산으로는 총 두개가 있으며 다음과 같다.

1. Union 함수
   • 서로 다른 두 트리를 합친다
2. Find 함수
   • 노드를 찾아서 반환한다

Union 함수

서로 다른 두 트리를 합치는 연산으로, 각 트리의 루트 노드를 비교하여 둘 중 작은 루트 노드를 기준으로 합치게 된다. 따라서 사전에 find연산이 필수적으로 들어가야한다.

# 두 원소가 속한 집합을 합치기
def union_parent(parent, a, b):
    a = find_parent(parent, a)
    b = find_parent(parent, b)
    if a < b:
        parent[b] = a
    else:
        parent[a] = b

Find 함수

find 연산은 어떤 노드를 인자로 넘겼을 때, 해당 노드의 루트 노드를 반환하는 연산으로, 실 사용 예로는 임의의 두 노드가 연결되어 있는지(루트 노드가 같은지) 확인할 때 쓰이며, 보통 재귀 호출의 형태로 구현한다. 시간 복잡도 효율을 높이기 위해서 find 연산에서 경로 압축 최적화를 진행한다.

# 특정 원소가 속한 집합을 찾기
def find_parent(parent, x):
    # 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
    if parent[x] != x:
        return find_parent(parent, parent[x])
    return parent[x]

경로 압축 최적화

아래의 그림은 최적화를 진행하기 전과 후이다.

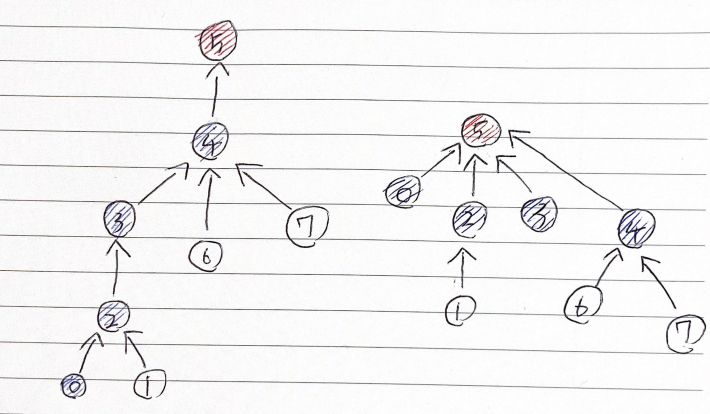
시간 복잡도

유니온 파인드의 시간 복잡도는 최적화 여부, 순서 등에 따라 매번 달라지기 때문에 구하기 까다롭다고 한다. 위의 코드를 보면 전체 시간 복잡도와 Union 함수의 시간 복잡도는 Find 함수의 시간 복잡도를 따라간다고 보면 된다.
실제 시간 복잡도는 O(α(N)) 라고 한다.