[Java] 백준 6091 핑크 플로이드

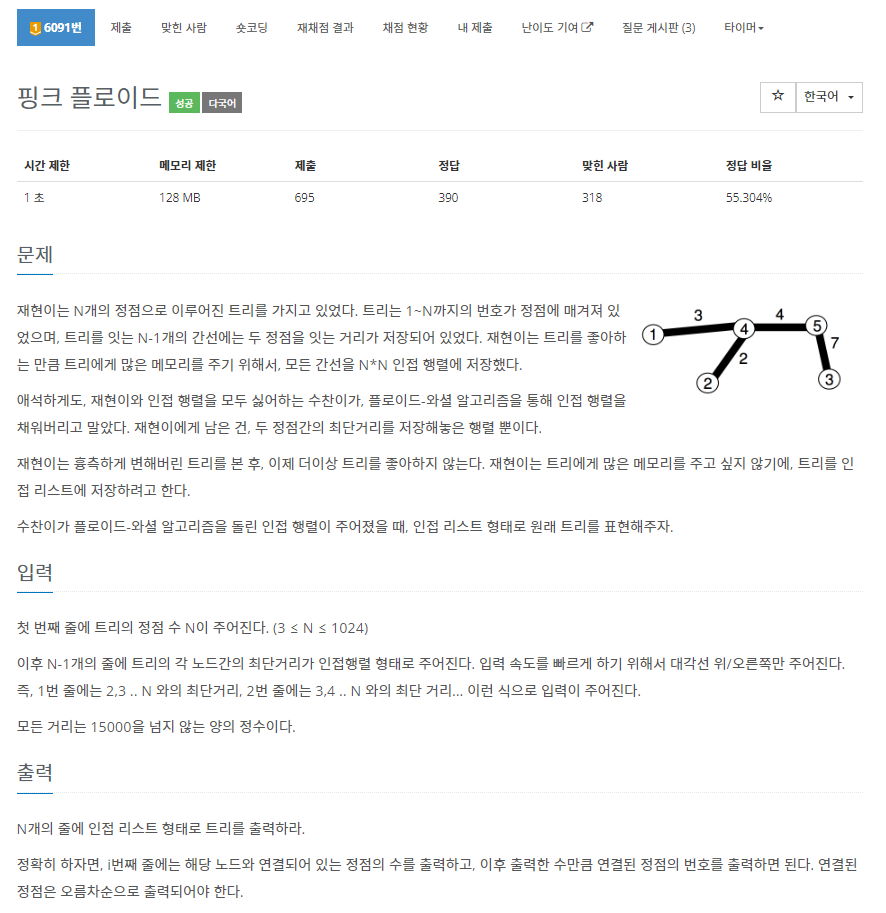
백준 6091 핑크 플로이드

풀이

주어진 예제를 기반으로 표를 인접 행렬을 표로 그려보면

입력	출력

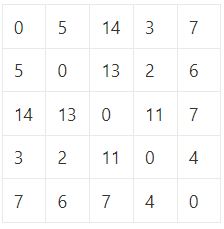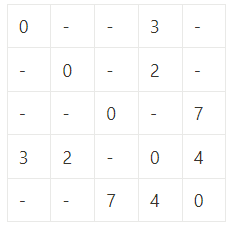이런 형태의 연결 관계를 보입니다.


이 출력 표를 기반으로 그래프를 그려보았습니다.

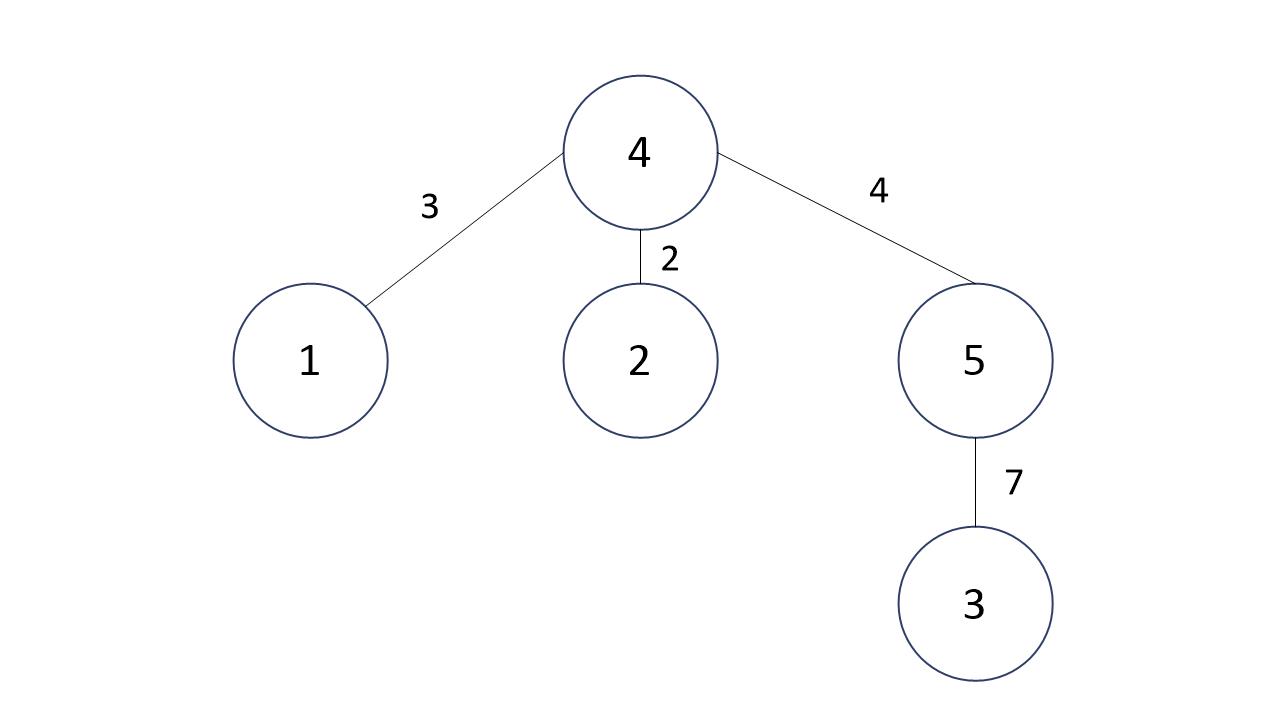
해당 표를 보면 알 수 있듯이 입력으로 주어진 인접 행렬을 기반으로 MST를 만들면 그것이 원본(출력)이 된다는 사실을 알 수 있습니다.

MST (최소 신장 트리)

MST란?

사이클없이 모든 간선을 연결하는 부분 그래프 중 간선 가중치의 합이 최소인 그래프

입니다.
모든 정점을 연결하며 사이클이 존재하면 안되기 때문에 MST에는 N개의 정점이 존재한다면 (N - 1)개의 간선만을 포함해야 합니다.
이러한 MST를 구하는 알고리즘으로는 Kruskal 알고리즘과 Prim 알고리즘이이 있습니다.

본 코드에선 Kruskal 알고리즘을 사용하였습니다.

Kruskal 알고리즘

Kruskal 알고리즘은 간선 중심으로 MST를 구하는 알고리즘입니다. 간선을 오름차순으로 정렬한 후, 가중치가 최소인 간선부터 선택하여 MST를 만듭니다. 이 때, 이미 MST에 포함된 정점과 아닌 정점을 구분하기 위해서 Union-find를 사용합니다. 간선의 시작 정점과 끝 정점이 서로 다른 집합에 속할 때만 해당 간선을 선택합니다. 간선이 E개 존재한다고 할 때, Kruskal 알고리즘의 시간 복잡도는 O( E log E )입니다.

코드

import java.io.*;
import java.util.*;

//백준 6091 핑크 플로이드
/*
 * 주어진 인접행렬을 통해 MST를 만들면 그것이 원본 인접리스트
 * */
public class Main {
	static class Node implements Comparable<Node> {
		int from;
		int to;
		int cost;
		public Node(int from, int to, int cost) {
			super();
			this.from = from;
			this.to = to;
			this.cost = cost;
		}
		@Override
		public int compareTo(Node o) {
			return this.cost - o.cost;
		}
	}
	
	static int parent[];
	
	private static boolean union(int a, int b) {
		a = find(a);
		b = find(b);
		
		if(a != b) {
			if(a < b) parent[b] = a;
			else parent[a] = b;
			return true;
		}
		return false;
	}
	
	private static int find(int a) {
		if(parent[a] == a) return a;
		else return parent[a] = find(parent[a]);
	}
	
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringBuilder sb = new StringBuilder();
		int N = Integer.parseInt(br.readLine());
		
		parent = new int[N + 1];
		
		for(int i = 0;i <= N;i++) parent[i] = i;
		
		String str[];
		PriorityQueue<Node> pq = new PriorityQueue<>();
		
		for(int i = 1; i < N;i++) {
			str = br.readLine().split(" ");
			for(int j = 0;j < str.length;j++) pq.add(new Node(i, j + i + 1, Integer.parseInt(str[j]))); 
		}
		
		ArrayList<Node> list = new ArrayList<>();
		
		//크루스칼 알고리즘을 통한 MST 구하기
		int cnt = 0;
		while(!pq.isEmpty()) {
			Node temp = pq.poll();
			
			if(union(temp.from, temp.to)) {
				cnt++;
				list.add(temp);
				if(cnt == N - 1) break;
			}
		}
		
		//원본 인접 리스트 만들기
		ArrayList<Integer> adjList[] = new ArrayList[N + 1];
		for(int i = 0;i <= N;i++) adjList[i] = new ArrayList<>();
		
		for(Node temp : list) {
			adjList[temp.from].add(temp.to);
			adjList[temp.to].add(temp.from);
		}
		
		for(int i = 1;i <= N;i++) {
			sb.append(adjList[i].size()).append(" ");
			Collections.sort(adjList[i]);
			for(int a : adjList[i]) sb.append(a).append(" ");
			sb.append("\n");
		}
		
		System.out.println(sb.toString());
	}
}