문제

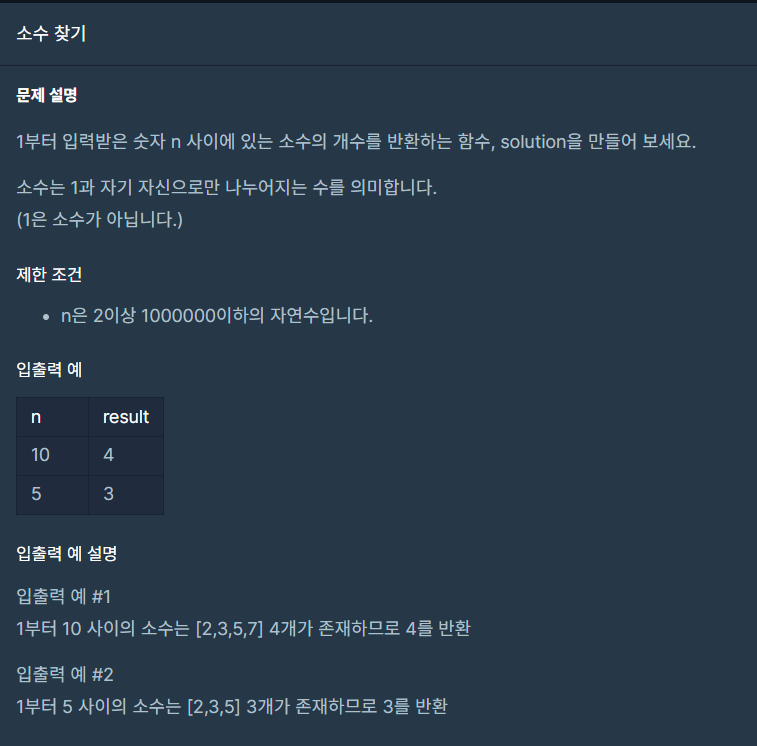
이번 문제는 말 그대로 입력 값 이하의 소수의 개수를 찾는 것이 목표인 문제이다.
문제는 어렵진 않지만 여기서 중요한 점은 시간 복잡도를 줄이는 것이 관건이였다.

이전 코드

function solution(n) {
    var answer = n-1;
    var divCheck;
    // 숫자 소수인지 2부터 하나씩 체크
    for(var i = 2;i<=n;i++){
      	//몇개 나누어졌는지 확인할 변수
        divCheck = 0;
      	//나누어지는 수는 divCheck++ 를 한다.
        for(var div = 2;div<=i;div++){
            if(i%div===0){
                divCheck++;
            }
          	//만약 나눠지는 수가 1보다 크다면 소수가 아니라 판단 소수 개수를 하나 줄이고 break
            if(divCheck>1){
                answer--;
                break;
            }
        }
    }
    
    return answer;
}

이때 문제가 이중for문 을 사용해서 시간복잡도가 n^2 이 되어서 시간초과가 발생했다.
이를 해결하기 위해, 고민을 하던 중 소수를 찾는 방법인 에라토스테네스의 체 방법을 알게 되었고, 이를 이용하게 되었다.

에라토스테네스의 체?

이는 소수를 찾는 방법인데, 이에 대한 알고리즘은 아래와 같다.
1. n+1의 이하의 배열을 만들고, 이의 기본값은 true 를 했다.
2. 2부터 시작해서, 소수를 찾는다.
3. 소수 기준으로 배수를 모두 false로 돌린다.
4. 이러한 과정을 n까지 진행한다.

자세한 내용은 아래 링크를 참고하면 좋다.

에라토스테네스의 체란? (위키백과) https://ko.wikipedia.org/wiki/%EC%97%90%EB%9D%BC%ED%86%A0%EC%8A%A4%ED%85%8C%EB%84%A4%EC%8A%A4%EC%9D%98_%EC%B2%B4

해결 코드

function solution(n) {
  var answer = 0;
  //에라토스테네스의 체 이용
  // n+1의 이하의 배열을 만들고, 이의 기본값은 `true` 로 설정
  var checkArr = new Array(n + 1).fill(true);

  // 2부터 n까지 체크
  for (var i = 2; i <= n; i++) {
    // checkArr[i] 가 소수(true)라면
    if (checkArr[i]) {
      answer++;
      //거기에 대한 배수에 대한 값을 모두 false로 함.
      for (var j = i + i; j <= n; j += i) {
        checkArr[j] = false;
      }
    }
  }

  return answer;
}

소수를 하나 찾더라도, 맨 처음 코드와 같이 짤 수도 있다. 돌아는 가겠지만 첫번째 코드와 두번쨰 코드는 효율성 면에서 차이가 있을 것이다. 이러한 시간 복잡도를 고려한 알고리즘을 짜는게 중요하다고 생각이 들었다.