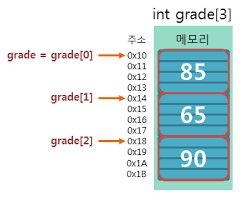
배열
데이터를 연속적인 메모리 공간에 할당.
숫자 인덱스로 O(1)의 시간복잡도로 참조 가능. grade[2] = 90;
하지만 연속된 공간에 데이터를 할당하기에 삽입 삭제 시에 O(N)의 시간복잡도를 갖는다.
정적배열
고정된 크기의 배열.
동적배열
유동적인 크기의 배열.
자바에서 동적 배열은 Vector와 ArrayList가 있음
Vector는 동기화 문제를 고려하여 멀티쓰레드 환경에서 안전하나 ArrayList보다 느림.
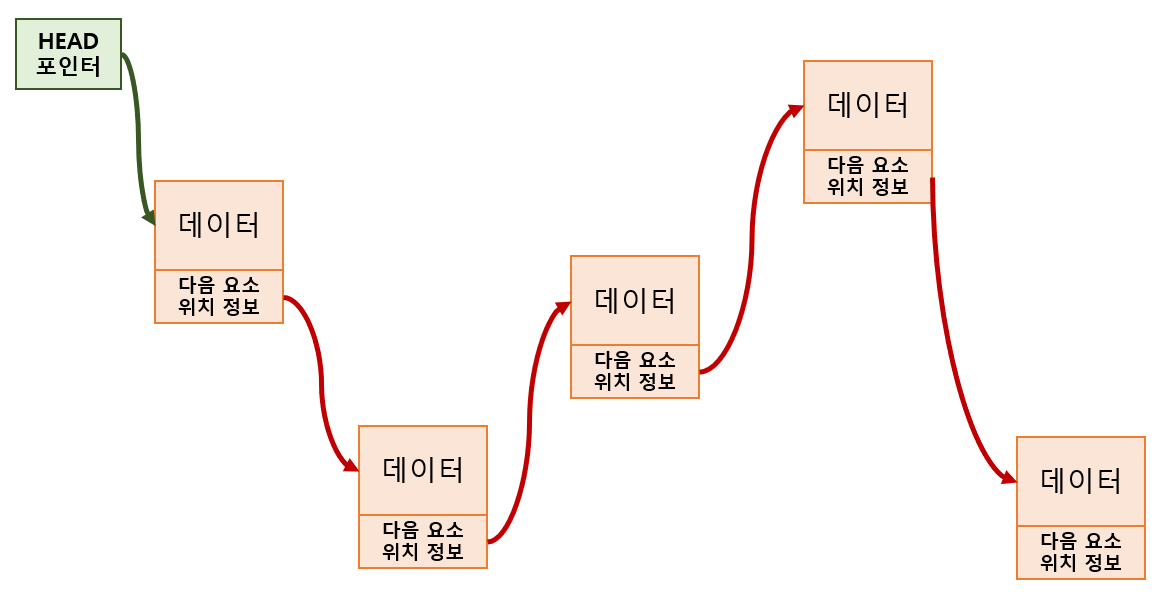
연결리스트
데이터를 독립적인 공간에 할당.
데이터만 저장하지 않고
데이터와 다음 데이터의 주소를 가지고 있는 노드라는 형식으로 저장.
인덱스 접근이 불가능해 특정 데이터를 참조하려면 O(N)의 시간복잡도를 갖는다.
독립적인 공간에 노드형식으로 저장하기 때문에
삽입과 삭제시에 O(1)의 시간복잡도를 갖는다.
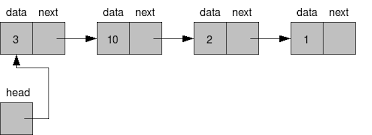
싱글 연결리스트
노드들끼리 단방향으로 연결된 리스트
이중 연결리스트
노드들끼리 양방향으로 연결된 리스트
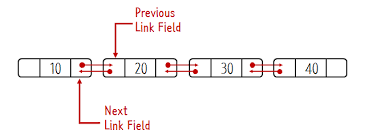
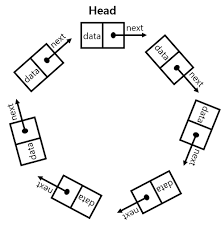
원형 연결리스트
마지막 노드와 첫 노드가 연결된 리스트
(싱글, 이중 둘 다 가능)
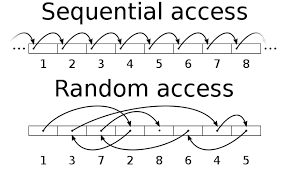
순차, 직접 액세스
배열은 직접(Random) 액세스로 빠른 접근
연결리스트는 순차(Sequntial) 액세스로 느린 접근
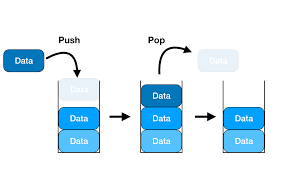
스택
먼저 들어온 것이 나중에 나가는(LIFO = 후입선출) 자료구조
탐색, 참조는 모두 O(n)의 시간 복잡도를 갖는다.
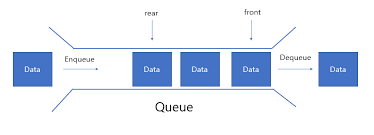
큐
먼저 들어온 것이 나중에 나가는(FIFO = 선입선출) 자료구조
스택과 마찬가지로 탐색, 참조는 모두 O(n)의 시간 복잡도를 갖는다.
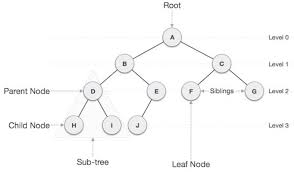
트리
노드와 간선으로 이루어지고,
계층 구조(부모 노드 자식 노드의 관계)를 가지는
사이클이 없는 비선형 자료구조.
루트노드 - 가장 위의 노드
리프노드 - 자식이 없는 노드
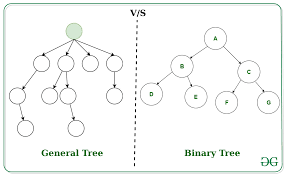
이진트리 - Binary Tree
각각의 노드의 자식 노드가 2개 이하인 트리
사진의 루트노드의 자식노드의 수를 보면 일반 트리와의 차이를 알 수 있다.
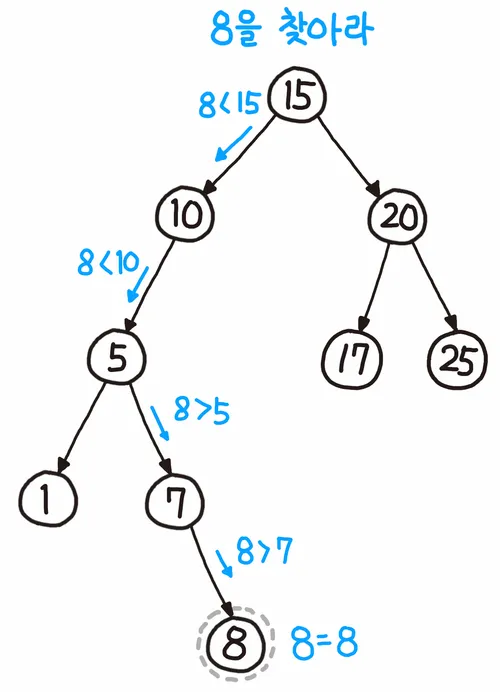
이진탐색트리 - Binary Search Tree(BST)
왼쪽에는 부모 노드보다 작은 수, 오른쪽에는 부모 노드보다 큰 수를 넣는 규칙을 적용한 트리이다.
그림을 보면 항상 부모노드는 왼쪽 자식 노드보다 크고 오른쪽 자식노드보다 작다.
이진 탐색 트리 불균형 문제
이진 탐색 트리는 아래와 같이 불균형하다면 탐색시에 O(N)의 시간복잡도를 갖는다.
만약 균형이 잡혀있다면 탐색시에 O(logN)의 시간복잡도를 갖는다.( = "트리의 높이+1"만큼만 탐색하면 된다.)
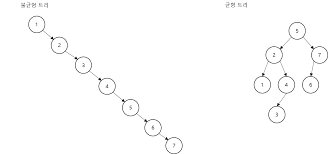
균형 이진 탐색 트리(밸런스 이진 탐색 트리)
불균형 상태의 이진탐색트리는 탐색 시에 O(N)의 시간복잡도를 갖는다.
트리 회전 등의 방식을 사용하여 트리의 균형을 맞춰서 O(logN)의 시간복잡도를 갖도록 만드는 트리이다.
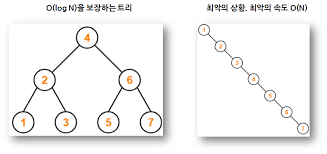
밸런스 트리의 종류로는 AVL트리,
DB 인덱스에 사용되는 B트리,
자바에서 Map, Set, HashTable 등에 사용되는 레드블랙트리가 있다.
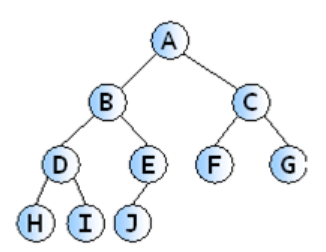
완전 이진 트리 - Complete Binary Tree
왼쪽부터 데이터를 채워 넣는 이진 트리.
사진처럼 A부터 J까지 알파벳 순서대로 데이터를 해당 위치에 놓는 트리이다.
A위치에 데이터1을 놓고 C위치에 데이터2를 놓으면 이는 완전이진트리가 아니다. 왼쪽에 있는 B 위치부터 데이터를 채워넣어야 한다.
힙
완전이진트리 + 규칙의 자료구조
최대힙 규칙 : 부모는 항상 자식보다 큼
최소힙 규칙 : 부모는 항상 자식보다 작음
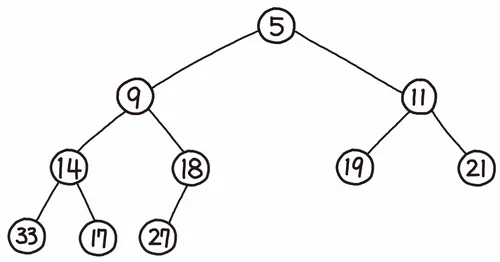
사진은 최소힙이다.
힙 vs 이진 탐색 트리
이진 탐색 트리는 부모의 왼쪽 자식은 부모보다 작고, 오른쪽 자식은 부모보다 크다.
힙은 단순하다. 왼쪽 오른쪽 구분없이
최대힙은 자식이 부모보다 크면되고
최소힙은 자식이 부모보다 작으면 된다.
사진의 14 노드를 살펴보자.
왼쪽 자식은 33, 오른쪽 자식은 17이다.
만약 이진 탐색 트리였다면 14의 자식인
33과 17은 모두 오른쪽 서브 트리로 들어갈 것이다.
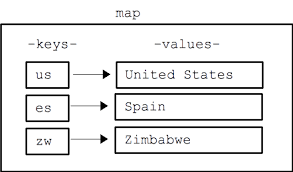
맵
키와 값의 쌍으로 데이터를 저장하는 자료구조.
레드 블랙 트리로 구현된다.
자동으로 정렬된다.
자바의 TreeMap을 생각하자.
레드 블랙 트리로 구현되기 때문에 삽입, 삭제, 조회는 O(logN)의 시간복잡도를 갖는다.
셋
데이터의 중복을 허용하지 않는 자료구조.
레드 블랙 트리로 구현된다.
자동으로 정렬된다.
자바의 TreeSet을 생각하자.
레드 블랙 트리로 구현되기 때문에 삽입, 삭제, 조회는 O(logN)의 시간복잡도를 갖는다.
해시테이블
해시 함수를 통해 키로 쓸 데이터를 해싱해서 해시 값을 만들고,
해시를 키로 사용하여 키와 값 쌍으로 데이터를 저장하는 자료구조
키와 값을 같이 저장한다
보통의 경우 해시 테이블의 조회, 탐색, 삭제의 시간복잡도는 O(1)을 갖는다.
최악의 경우 해시 테이블의 조회, 탐색, 삭제의 시간복잡도는 O(n)을 갖는다. (뒤에서 설명함)
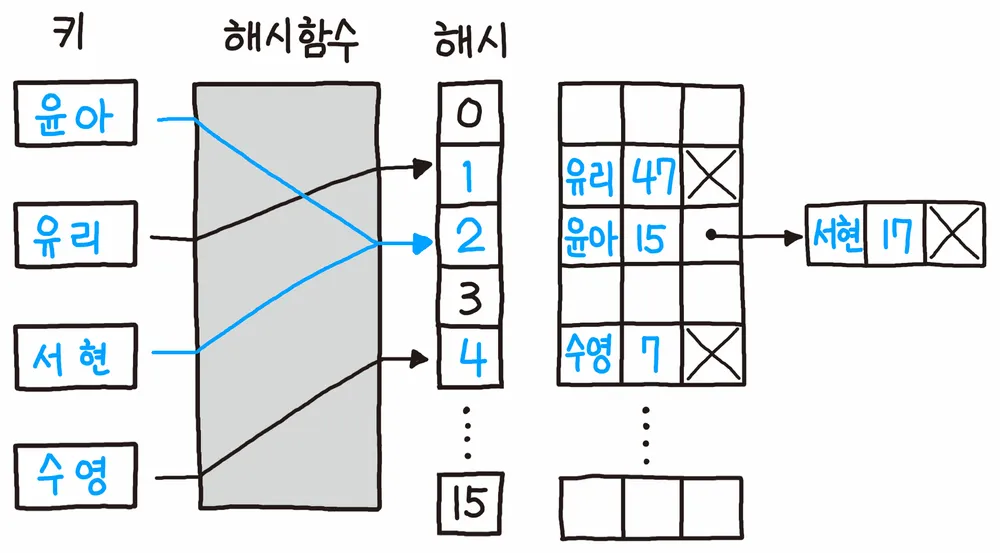
그림과 같이 해시값은 한정된 범위의 값을 가진다.
그림에서는 0~15의 해시 값을 가지고 있다.
즉 해시테이블의 크기(capacity)는 16이다.
자바에서는 기본적으로 크기를 16으로 잡고 데이터가 많아지면 resize를 한다.
해시함수와 모듈러 연산
해시함수는 임의의 값을 넣으면 정수 값으로 변환해주는 함수이다.
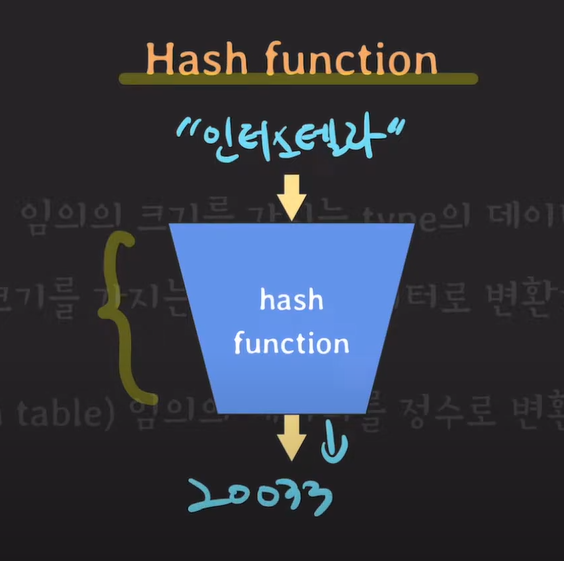
출처 - https://www.youtube.com/watch?v=ZBu_slSH5Sk
만약 인터스텔라라는 키로 쓸 데이터를 넣으면 20033이라는 값으로 변환해주는 것이다.
앞서 해시값은 한정된 범위의 값을 가진다고 했다.
위의 그림에서는 0~15의 범위를 갖고 있다.
20033은 이 범위를 초과하는 값이기 때문에 모듈러 연산(20033 % 16)을 통해 0~15 범위의 값으로 만들고 그 곳에 데이터를 저장한다.
충돌
해시 값은 한정된 범위의 값을 가지기 때문에 다른 키가 같은 해시 값을 가질 수 있다.
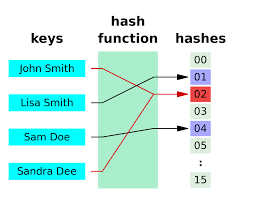
그림에서는 John Smith, Sandra Dee가 2라는 키가 해시함수를 통해 2라는 같은 해시 값이 나왔다.
이런 경우 충돌이 발생한 것이다.
충돌은 막을 수 없다. 그래서 이를 해결하기 위한 2가지 방법이 있다.
충돌 해결: 오픈 어드레싱
충돌 시에 비어있는 다른 곳에 저장하는 방식
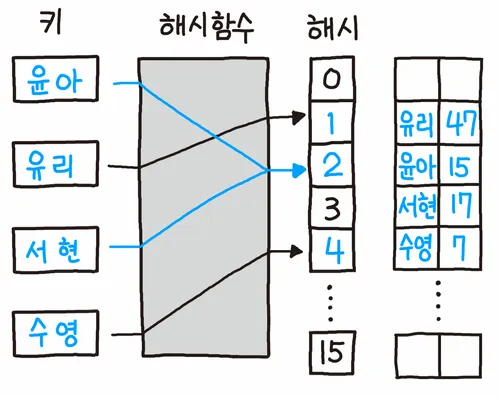
그림에서는 윤아와 서현의 해시 값이 2로 충돌이 발생했다.
이에 따라 서현은 2의 다음 해시인 3에 저장됐다.
장점 : 비어있는 곳을 채워 메모리를 효율적으로 사용.
단점 : 비어 있는 곳을 탐색하는 규칙을 정해줘야 함.(사진에서는 해시를 +1하며 탐색함)
충돌 해결: 체이닝
충돌 시에 연결 리스트에 저장하는 방식

그림에서는 윤아와 서현의 해시 값이 2로 충돌이 발생했다.
이에 따라 서현은 2에 저장되어 있는 윤아의 뒤에 연결 리스트 형식으로 저장했다.
장점 : 구현이 단순함.
단점 : 최악의 경우(한 곳에 데이터가 몰리면) 탐색 시 O(N)의 시간복잡도를 가짐
체이닝 단점
해시 테이블의 조회, 탐색, 삭제의 시간복잡도는 O(1)이지만,
윤아, 유리, 서현, 수영이라는 키의 해시가 모두 2가 되는 최악의 상황을 가정해보자.
해당 상황에서 특정 데이터를 탐색하면 결국 연결리스트의 탐색과 다를게 없다.
즉 최악의 경우 O(N)의 시간 복잡도를 갖게 되는 것이다.
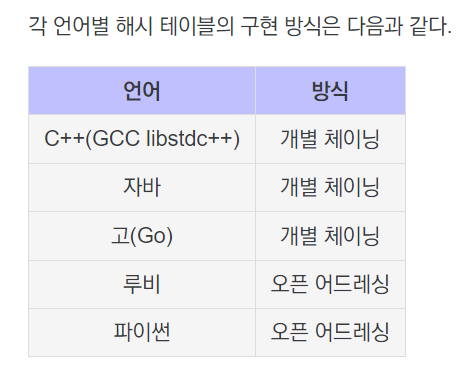
자바에서는...
자바에서는 충돌을 체이닝 방식으로 해결하고 있는데,
자바 8부터 해시 버킷의(= 특정 해시에 저장된) 항목 수가 임계값을 넘어가면 연결 리스트를 레드 블랙 트리로 전환하여 시간 복잡도를 O(logN)으로 줄인다.
HashMap, HashSet 등의 경우 레드블랙트리로 전환하지만,
HashTable의 경우 전환하지 않기 때문에 최악의 경우 O(N)의 시간복잡도를 갖는다.
출처
인프런 - CS 지식의 정석
위키백과, 나무위키 등등...