귀무가설, 대립가설
- 귀무가설(null hypothesis)
대립가설(alternative hypothesis) - 귀무가설은 틀림을 증명하려는 가설이고, 대립가설은 예상을 반영하는 (맞음을 검증하고자 하는) 가설이다.
- 귀무가설은 대립가설의 역
- 귀무가설 기각을 통해 대립가설 채택
(귀류법같은 방식)

- 하지만 귀무가설의
귀무가설의 도입 배경
- 참이 아님을 증명하는 것이 참임을 증명하는 것보다 훨씬 쉽기 때문.
- 귀무가설을 “올바르게” 서술하는 것이 대립가설을 “정확하게” 서술하는 것 보다 실패할 가능성이 적다.
- 우리는 모수에 대해서 알 수 없으며, 연구에 있어 주관성이 개입되어선 안되기 때문.
( 이러한 관점의 대척점 : 베이지안 통계 )대립가설을 간접적으로 이용하는 방법 : 구간 추정
대립가설을 직접적으로 이용하는 방법 : Bayes factor
귀무가설을 기각시키는 방법
p-value
- 어떤 분포(귀무가설)을 가정했을 때 그 분포에서,
우리가 얻은 표본에 대한 검정통계량 이상으로 나올 확률
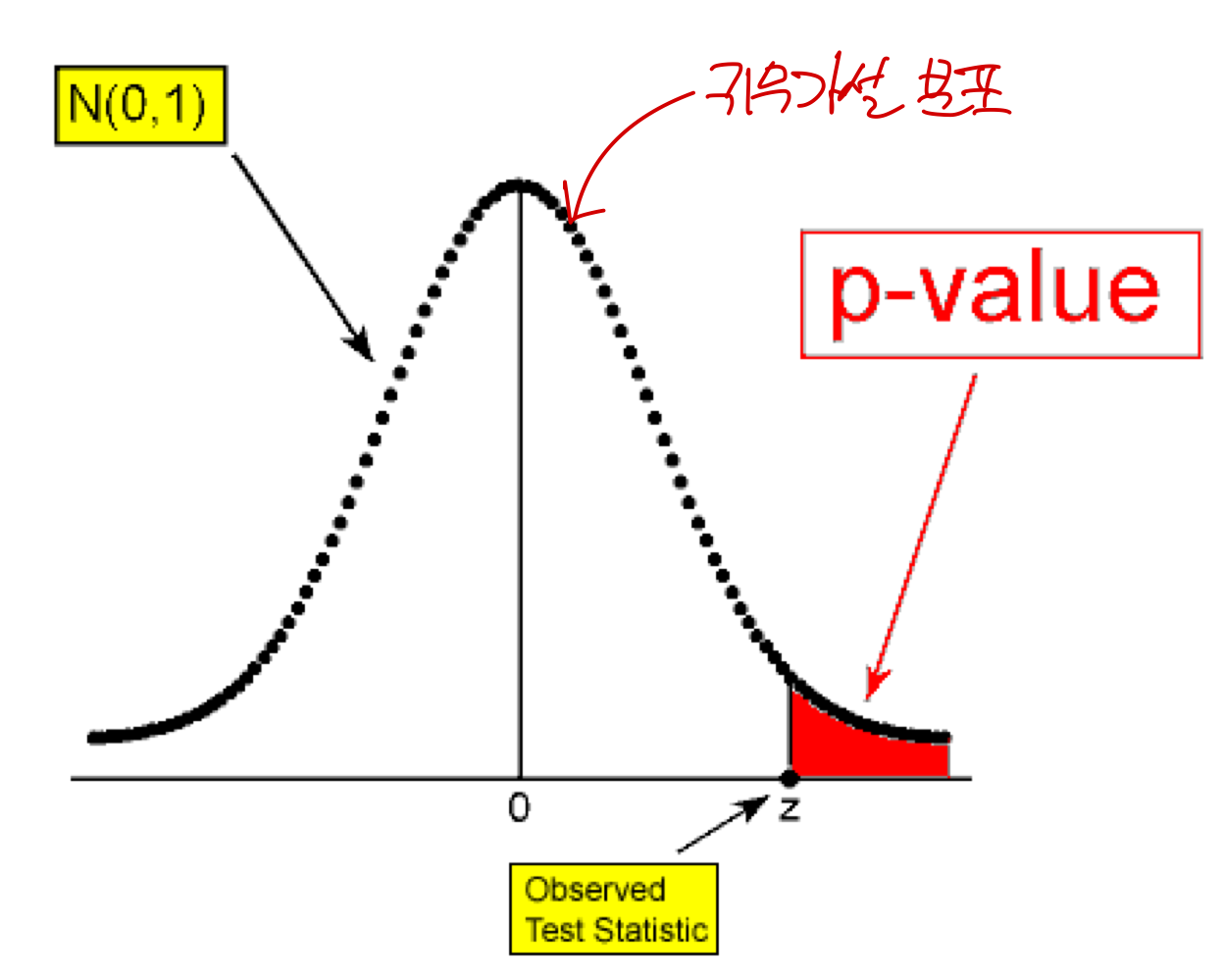
유의수준, 유의확률, 기각역
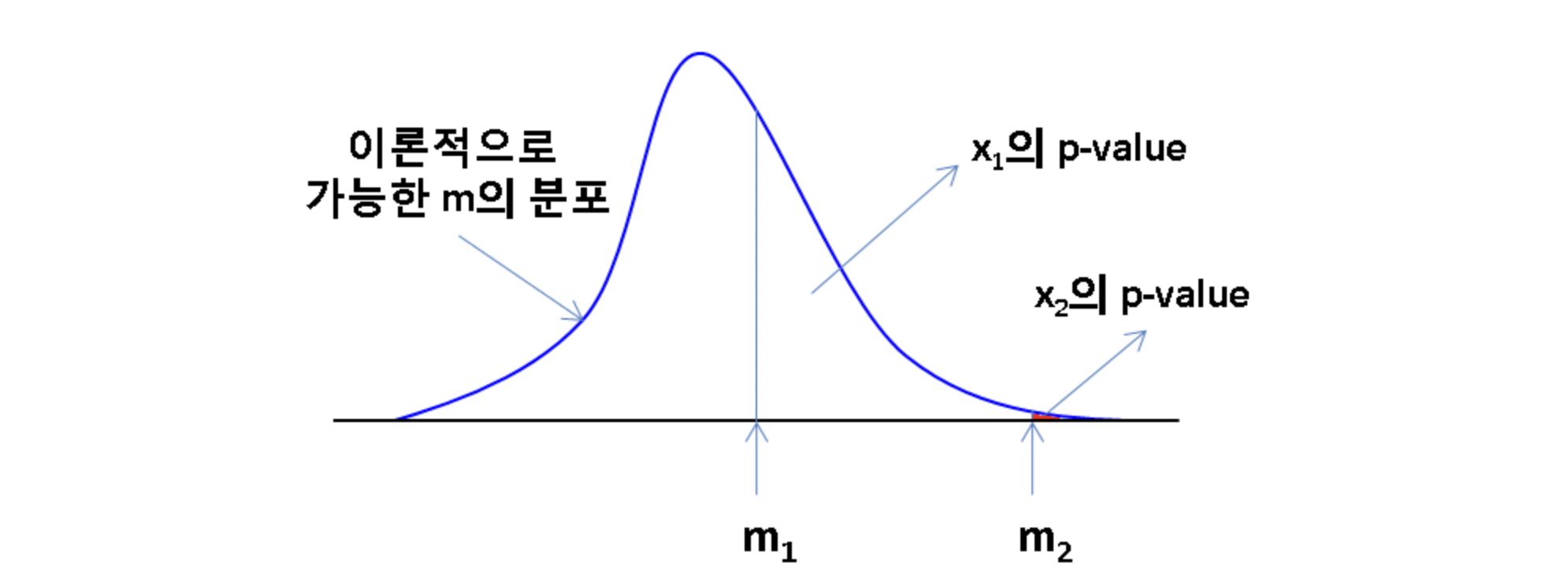
- 귀무가설에 대해, p-value가 매우 작다면 관찰된 통계량같은 (극단적인) 값이 관찰된 확률이 매우 작다는 뜻이므로
-> 귀무가설을 기각한다. - p-value, p : "유의확률"
- 이때 p-value가 충분히 작은지 판단하는 임계값이 "유의수준"이다.
- 보통 유의수준을 0.05로 가져간다. (5%)
- p가 유의수준 보다 작아서, 귀무가설을 기각하게 되는 영역을 "기각역"이라 한다.
p < 유의수준 : 귀무가설 기각
귀무가설 기각
- 단측 검정
- 모집단의 평균이 A보다 크다고(작다고) 생각하는 경우
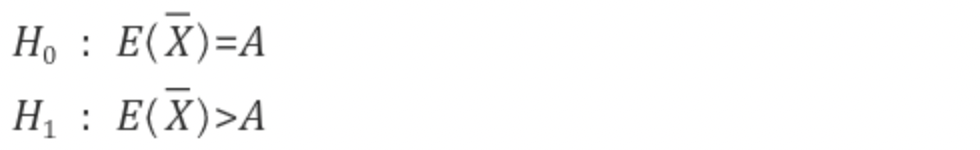
- 귀무가설 : 평균이 A인 분포
- 기각역 : 오른쪽에만 존재 (5%)
- 즉, p-value < 0.05 : 귀무가설 기각
- 모집단의 평균이 A보다 크다고(작다고) 생각하는 경우
- 양측 검정
- 모집단의 평균이 A가 아니라고 생각하는 경우
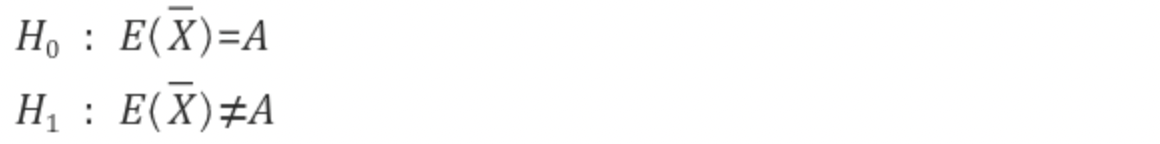
- 귀무가설 : 평균이 A인 분포
- 기각역 : 양쪽에 존재 (각 2.5% 씩)
- 즉, p-value < 0.025 : 귀무가설 기각
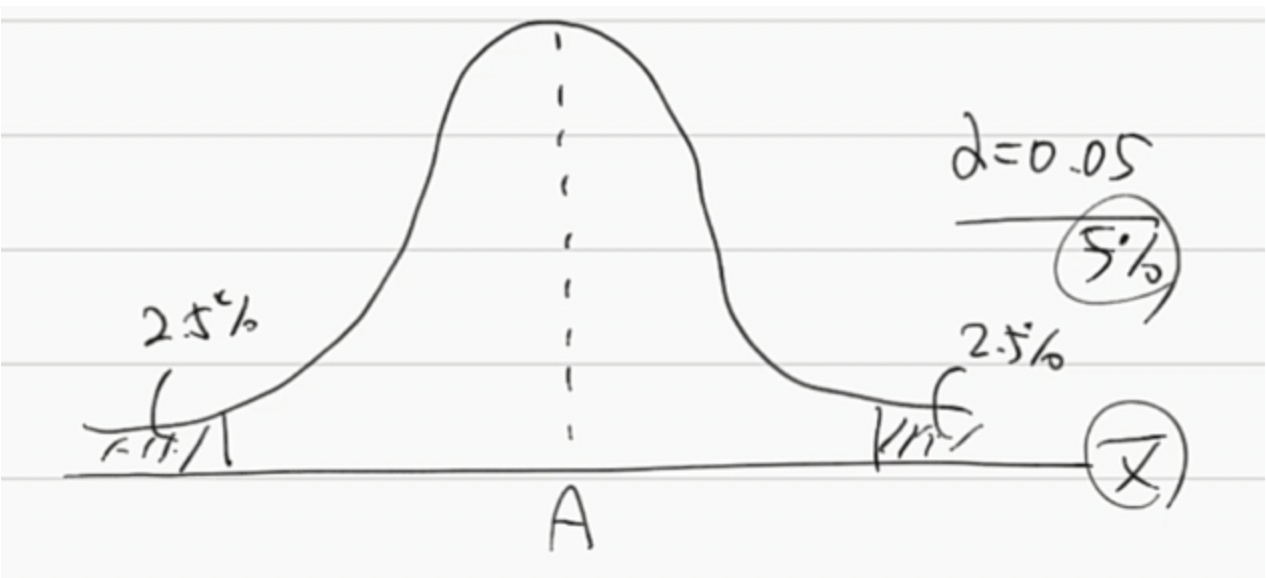
- 모집단의 평균이 A가 아니라고 생각하는 경우