Collaborative Metric Learning (WWW 2017)

Abstract

• 유저의 preference 뿐만이 아니라, user-user similarity와 item-item similarity를 합쳐 추천시스템에 metric learning을 적용한 논문

Introduction

• distance 등의 metric은 기계학습에서 매우 중요한 요소 중 하나이며, 이를 바탕으로 similarity와 dissimilarity를 계산함
• 유사도 기반 방법은 Matrix Factorizaion과 유사, user/item vector의 dot product를 통해 rating을 예측
• 다만 진정한 컨셉의 similarity에서, MF는 삼각 부등식을 만족하지 않기에 유사도 기반 방법이라 말할 수 없음
• 결과적으로 suboptimal한 성능을 보임 (실험으로 증명)
• 우리는 이를 해결하고, user/user와 item/item similarity를 반영한 CML(Collaborative Metric Learning)을 제시
• Accuracy, Top-K Recommender에서 sota를 달성했으며, user의 preference를 더 잘 표현함을 실험적으로 증명함

Background

Metric Learning

• $\mathrm{X} =$ {$\mathrm{x_1}, \mathrm{x_2}, ... ,\mathrm{x_n}$} $\in\mathbb{R^m}$

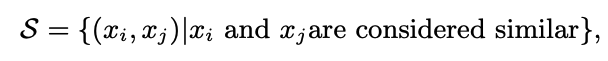
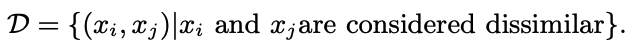
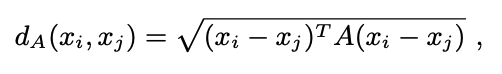
• 다음과 같은 마할라노비스 거리를 계산하여 metric learning

• 만약 $\mathrm{A} \in \mathbb{R^{m*m}}$ 일 경우에는 PSD 이므로,

  • $\mathrm{x}$를 $\mathbb{R^m}$에 정사영하는 것과 같음

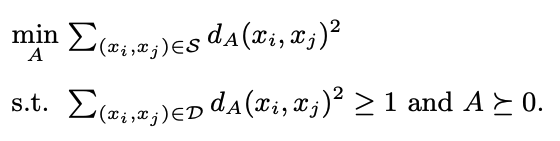
• 수 많은 방식이 존재하나, 다음 방식으로 주로 최적화

Metric Learning for kNN

• distance metric을 통해 kNN을 학습할 때, k개의 이웃만 동일한 레이블로 판단하게 하는 metric만 학습하면 이는 충분하다는 것이 알려짐
• 우리는 추천할 kNN 항목을 찾는 것이므로, 이를 채택할 것

large margin nearest neighbor (LMNN)

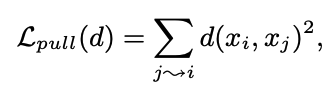
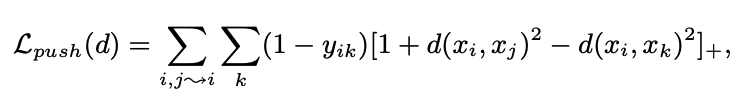
• 상기한 두 term을 loss function으로 사용하는 knn 모델
• j -> i는 i의 이웃인 j
• pull loss를 통해 이웃들을 끌어당기고, push loss로 imposter를 멀리 보내는 방식으로 학습
• $\mathrm{y_{ik}} = 1$ when $\mathrm{i=k}$ are same class
  otherwise 0
• $\mathrm{[z]_+} = max(z,0)$
• semidefinite programming을 통해 학습

Collaborative Filtering

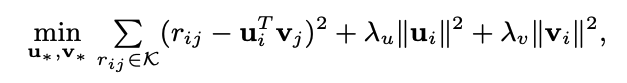
• 다음 식을 통해 학습
• implicit 한 데이터는 positive feedback만 존재하기에 trivial한 솔루션에 도달하거나 상호작용 하지 않은 데이터를 negative하게 처리하는 문제가 있었음
• weighted regularized matrix factorization, BPR 등으로 일부 해결하였으나 BPR loss는 낮은 rank의 item을 충분히 penalize하지 못하기에 suboptimal한 result
• 우리는 weighted ranking loss를 사용해 이를 해결하고자 함

Collaboraive Metric Learning

• explicit feedback에서 implicit feedback으로 넘어오는 과정에서 rating matrix를 예측하는 것이 아닌, user's relative preference를 포착하는게 더 중요해짐
• 우리의 모델은 interaction한 item과 user를 pull하고, negative를 push하는 과정으로 학습
• 이는 곧, traiangle inequality로 인해 비슷한 아이템을 선호한 user가 묶이고, 유저의 선호가 유사한 아이템들 끼리 묶일 것
• 최종적으로 유저가 이전에 사용한 아이템, 유저와 비슷한 선호의 유저가 사용한 아이템이 neighbor가 될 것
• 즉 user, item 쌍의 학습을 통해 직접 관찰되지 않은 user/user와 item/item의 관계 또한 학습하는 것

Model Formulation

• user i, item j
  $\mathrm{u_i,v_j} \in \mathbb{R^r}$
  
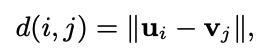
• distance measure

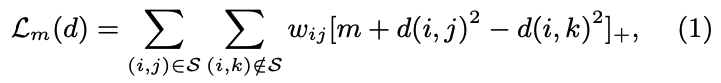
• j는 유저가 interaction한 아이템, k는 negative sample
• wij는 ranking losss weight, m은 0보다 큰 margin size

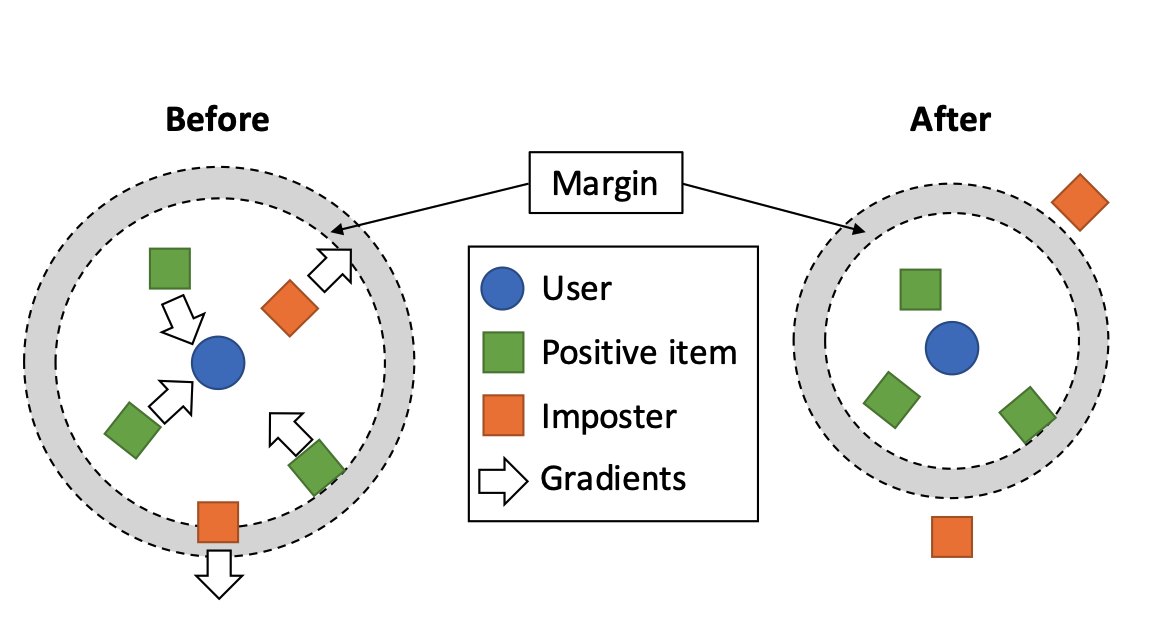
• user와 interaction한 아이템은 작은 원 안으로 들어오도록 update되고, imposter는 margin 밖으로 나가게 update
• 이 Loss function은 LMNN과 유사한 듯 보이나 3가지 차이점이 존재
  • user의 모든 target 이웃은 상호작용한 item이며, item의 이웃은 존재하지 않음
  • 하나의 아이템이 많은 사용자와 상호작용할 수 있고, 모든 사용자에게 가까이 끌어당기는 것은 불가능하기에 pull loss가 존재하지 않음
    • 그러나 push loss는 imposter가 user에게 가까이 있을 때 positive를 끌어당길 것
  • 우리는 weighted ranking loss를 채용하여 Top-K recommendation 성능을 증가하려 함

Approximated Ranking Weight

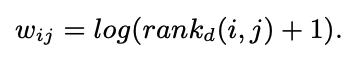
• $\mathrm{rank_d(i,j)}$ 는 item j에 대한 user i의 rank를 의미
• 이 식은 lower rank의 positive item에 상위 순위 항목보다 penalize를 주어 SOTA를 가능케 함
• 다만 gradient 계산에서 cost를 많이 소모
• 따라서 $\mathrm{N}$ 개의 negative sample과 positive item j를 비교하는 식으로 구함
• 결과적으로 $\mathrm{rank_d(i,j)} \approx \frac{J * M}{N}$
• 여기서 $\mathrm{J, M, N}$은 각각 Positive Item 개수, Imposter 개수, Negative Sample 개수를 의미
• User마다 Negative sampling을 하는 것이 비용적으로 낭비인 것처럼 보이지만, 실험적으로 positive item이 더 빠르게 high rank로 진입하는 것을 보여줌

Integrating Item Features

• 위에 식에서 $f(\mathrm{x_j})$는 raw input을 user-item space로 mapping하는 함수

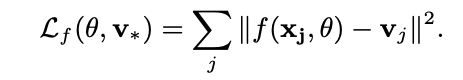
• 다음 식을 최적화 함으로써 함수 $\mathrm{f}$를 학습
• 이전 loss function과 병렬적으로 학습하여, 주로 $\mathrm{f}$는 MLP를 사용

Regularization

• kNN based 모델에서 높은 차원은 성능에 악영향을 미침 (차원의 저주, data point가 너무 멀리 떨어져 있음 등)

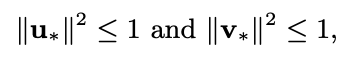
• 다음과 같이 regularization을 진행
• MF와 달리 L2 norm을 사용하지 않음
  • L2 norm은 origin으로 gradient를 끌어당기는데, 우리의 metric space에서 origin은 의미가 없기 때문

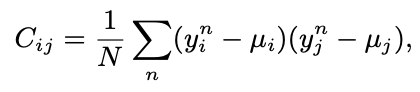
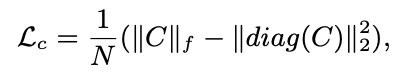
• $\mathrm{y^n}$ 은 user, item embedding을 lookup한 것
• $\mu_i = \frac{1}{N}\sum_ny_i^n$
• Covariance는 차원 간 선형 중복성의 척도이기에, 본 loss는 차원의 중복을 방지하고 공간을 효율적으로 사용하도록 만듬

Training Procedure

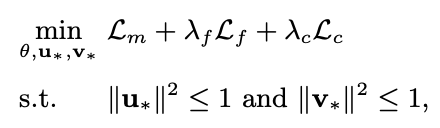
• $\lambda_f,\lambda_c$는 하이퍼 파라미터
• mini batch SGD로 진행 (Adagrad 사용)
• 다음 순서로 진행
  • $\mathrm{N}$개의 positive sample을 $\mathrm{S}$에서 추출
  • 모든 쌍마다 $\mathrm{U}$ negative items를 추출한 뒤, $\mathrm{rank_d(i,j)}$ 를 연산
  • 모든 쌍마다 hinge loss를 maximize하는 $\mathrm{k}$개의 negative item을 keep 하고, size $\mathrm{N}$의 mini-batch를 만듬
  • Gradient를 계산하고 adagrad에 따라 update
  • $\mathrm{u_*,v_*}$를 계산 (다음 식으로 정규화 $\frac{y}{max(\|y||,1)}$
  • 수렴할 때 까지 반복

Relation to Other Models

• 수식을 얼핏보면 BPR, 다른 matrix factorization과 유사한 것 처럼 보임
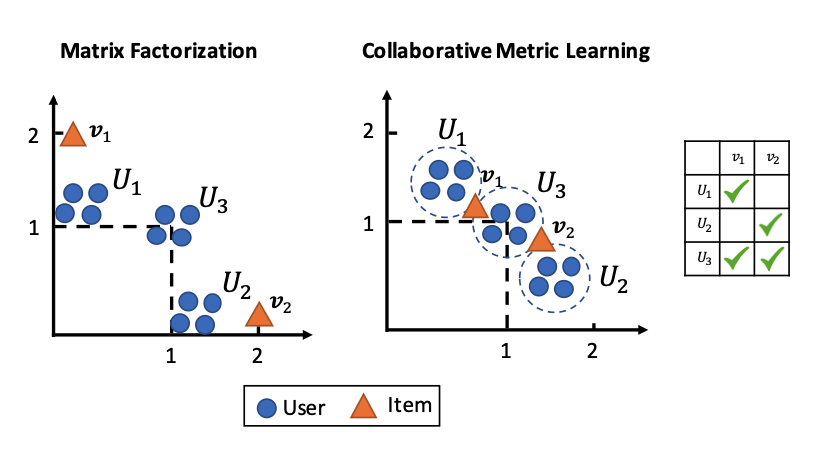
• 그러나 MF 기반 모델들은 Dot Product에 의존하기에, triangle inequality를 만족시키지 못함
• 따라서 두 가지 결과를 보임
  • 주 요인들을 잘 capture하지만, fine grained prefrenece를 capture하지 못함
  • item-item, user-user similarity를 capture하지 못함
• 상기된 figure가 typical한 MF, CML 모델의 결과인데 수식을 계산해보면 CML이 유저, 아이템 간 관계를 euclidean space에 더 잘 embedding 함