문제
지민이는 세계에서 가장 유명한 사람이 누구인지 궁금해졌다. 가장 유명한 사람을 구하는 방법은 각 사람의 2-친구를 구하면 된다. 어떤 사람 A가 또다른 사람 B의 2-친구가 되기 위해선, 두 사람이 친구이거나, A와 친구이고, B와 친구인 C가 존재해야 된다. 여기서 가장 유명한 사람은 2-친구의 수가 가장 많은 사람이다. 가장 유명한 사람의 2-친구의 수를 출력하는 프로그램을 작성하시오.
A와 B가 친구면, B와 A도 친구이고, A와 A는 친구가 아니다.
입력
첫째 줄에 사람의 수 N이 주어진다. N은 50보다 작거나 같은 자연수이다. 둘째 줄부터 N개의 줄에 각 사람이 친구이면 Y, 아니면 N이 주어진다.
출력
첫째 줄에 가장 유명한 사람의 2-친구의 수를 출력한다.
예제1
입력
3
NYY
YNY
YYN출력
2예제2
입력
3
NNN
NNN
NNN출력
0예제3
입력
5
NYNNN
YNYNN
NYNYN
NNYNY
NNNYN출력
4예제4
입력
10
NNNNYNNNNN
NNNNYNYYNN
NNNYYYNNNN
NNYNNNNNNN
YYYNNNNNNY
NNYNNNNNYN
NYNNNNNYNN
NYNNNNYNNN
NNNNNYNNNN
NNNNYNNNNN출력
8예제4
입력
10
NNNNYNNNNN
NNNNYNYYNN
NNNYYYNNNN
NNYNNNNNNN
YYYNNNNNNY
NNYNNNNNYN
NYNNNNNYNN
NYNNNNYNNN
NNNNNYNNNN
NNNNYNNNNN출력
8예제5
입력
15
NNNNNNNNNNNNNNY
NNNNNNNNNNNNNNN
NNNNNNNYNNNNNNN
NNNNNNNYNNNNNNY
NNNNNNNNNNNNNNY
NNNNNNNNYNNNNNN
NNNNNNNNNNNNNNN
NNYYNNNNNNNNNNN
NNNNNYNNNNNYNNN
NNNNNNNNNNNNNNY
NNNNNNNNNNNNNNN
NNNNNNNNYNNNNNN
NNNNNNNNNNNNNNN
NNNNNNNNNNNNNNN
YNNYYNNNNYNNNNN출력
6문제 분석
문제에서 말하는 "2-친구"에 대해 정의하자면...
- 사람이 직접적으로 친구일 때 : A와 B가 친구일 때 A의 2-친구는 B가 될 수 있다.
- 간접적으로 2-친구 관계를 형성할 때: 즉, A와 C가 친구이고, B와 C도 친구인 경우 A는 B의 2-친구이다.
그렇다면 "2-친구"를 어떻게 찾을까?
예를 들어 A,B,C,D,E,F의 총 6명의 친구가 있다고 해보자. 이때 A의 2-친구를 찾아보자
A -- B
| |
C -- D
|
E -- F
먼저 A의 친구는 B와 C이다.
A의 친구인 B의 친구는 D이다.
A의 친구인 C의 친구는 D이다.
따라서, A의 2-친구는 B, C, D이다.
문제에서 말하는 "유명한 사람"은 "2-친구"가 가장 많은 사람이라고 정의하고 있다.
즉, 어떤 친구로부터 가질 수 있는 "2-친구"가 최대가 될 수 있는 값을 찾아야 한다.
알고리즘 선택

그래서 플로이드 워셜 알고리즘이 무엇이냐
설명
a -> b 로 가는 비용과 a -> k -> b로 가는 비용 중 더 적은 것을 최단거리로 설정한다.
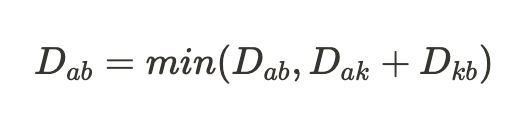
동작과정
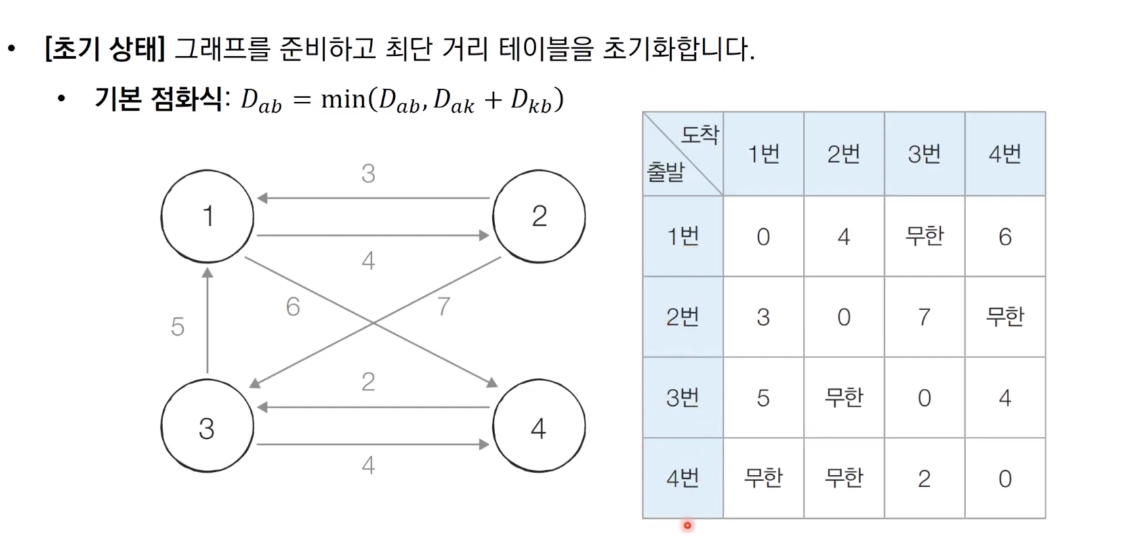
a → b로 가는 경로의 초기 비용을 설정.
행(row) - 출발점, 열(column) - 도착점에 대해 2차원 행렬을 만듦
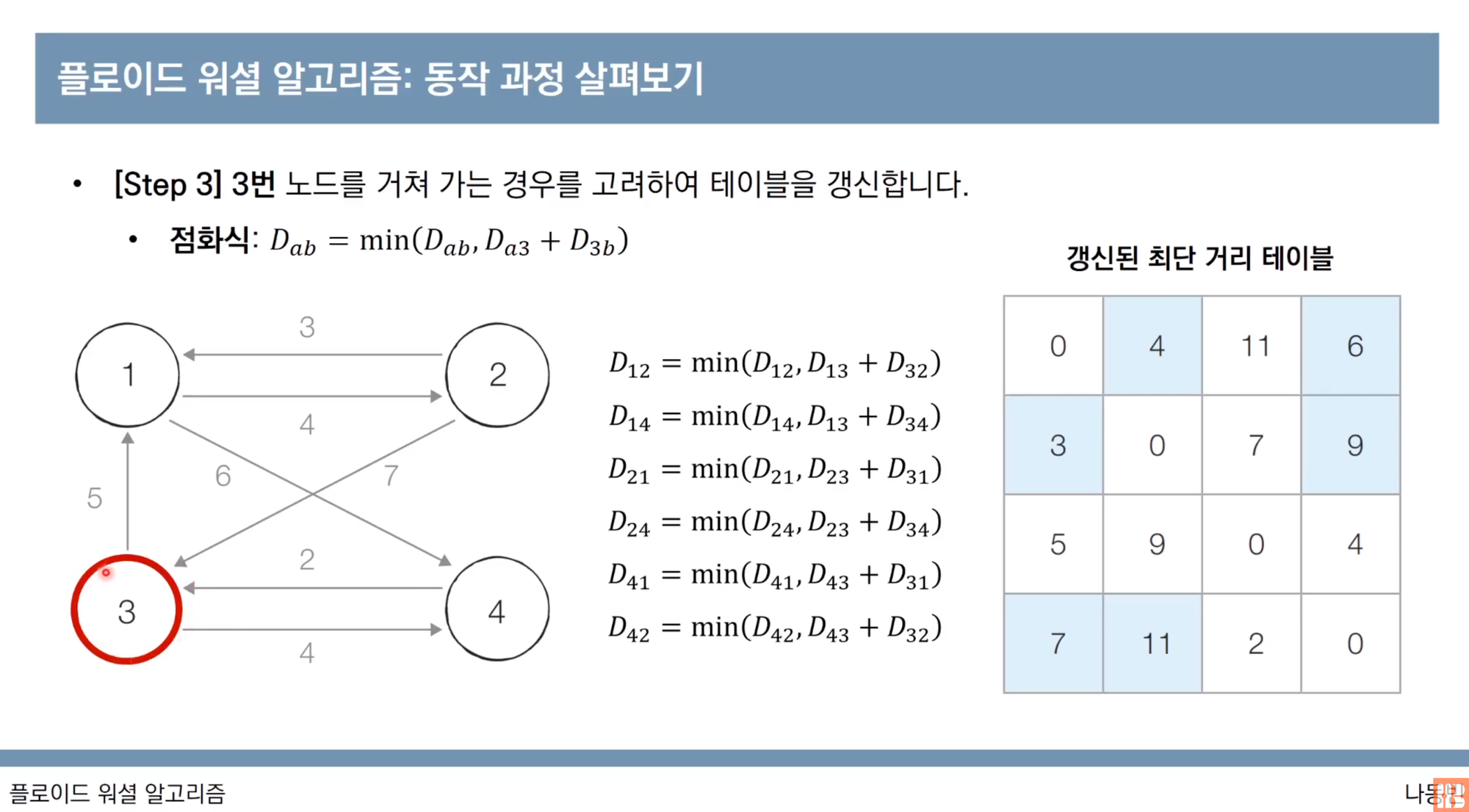
a가 1번 노드를 거쳐 b로 가는 경우에 min(a → b, a → 1 → b)를 계산하여 행렬을 갱신하면 된다.
그림에서는 a → 1 → b로 가는 경우는 1번 노드 자기 자신을 제외한 총 3개의 노드에서 3 x 2 = 6가지 이다.
예를 들어, 3번 -> 1번 -> 2번 노드로 가는 비용은 5 + 4 = 9이다. 3번 -> 2번 노드로 바로 가는 경우는 없기 때문에 무한에서 9로 업데이트 됨. 이렇게 나머지도 총 갱신하면 파란색 부분이 총 갱신된 부분이다. 아까 계산했듯이 6개만이 갱신이 되게 된다.
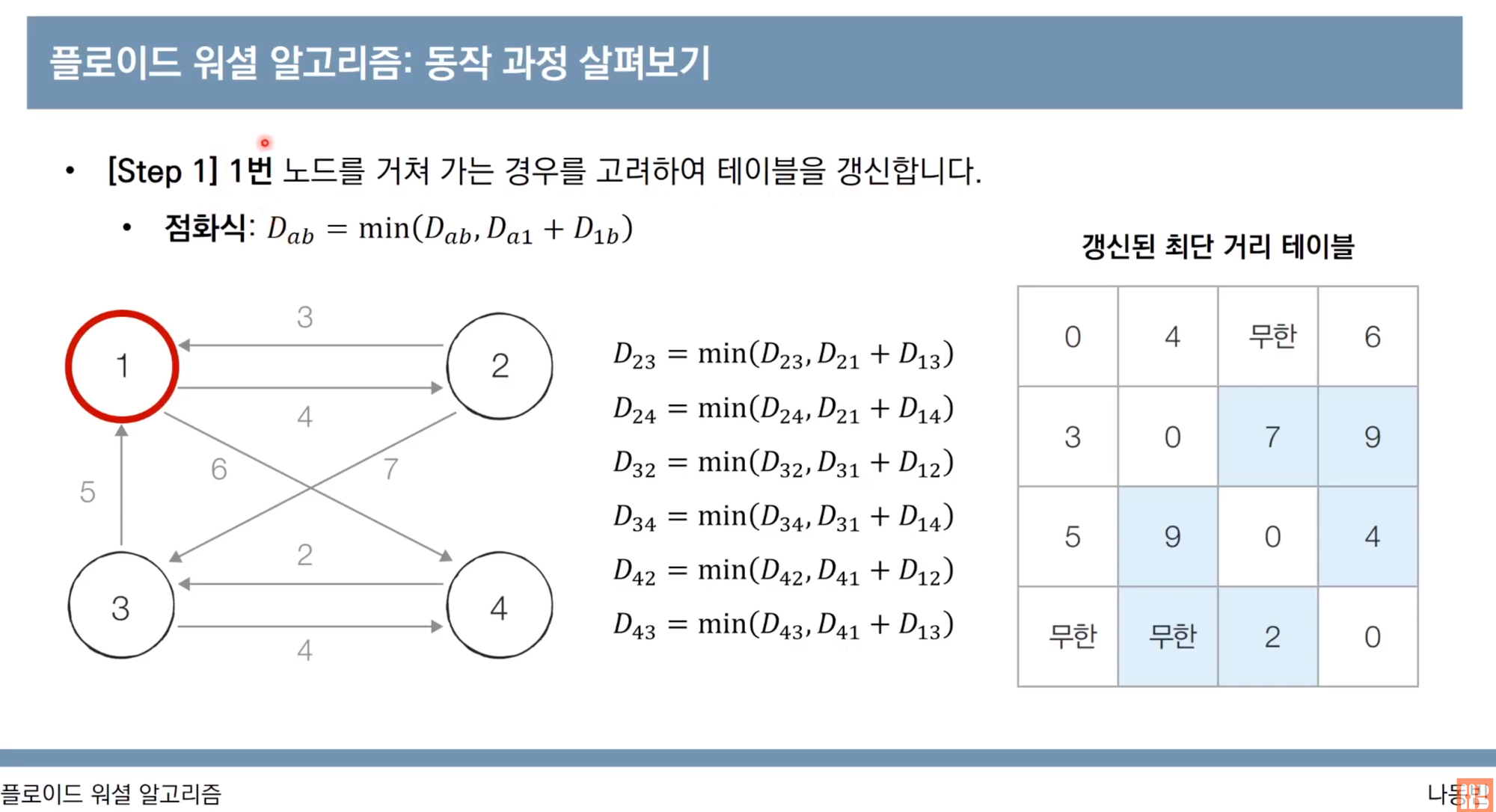
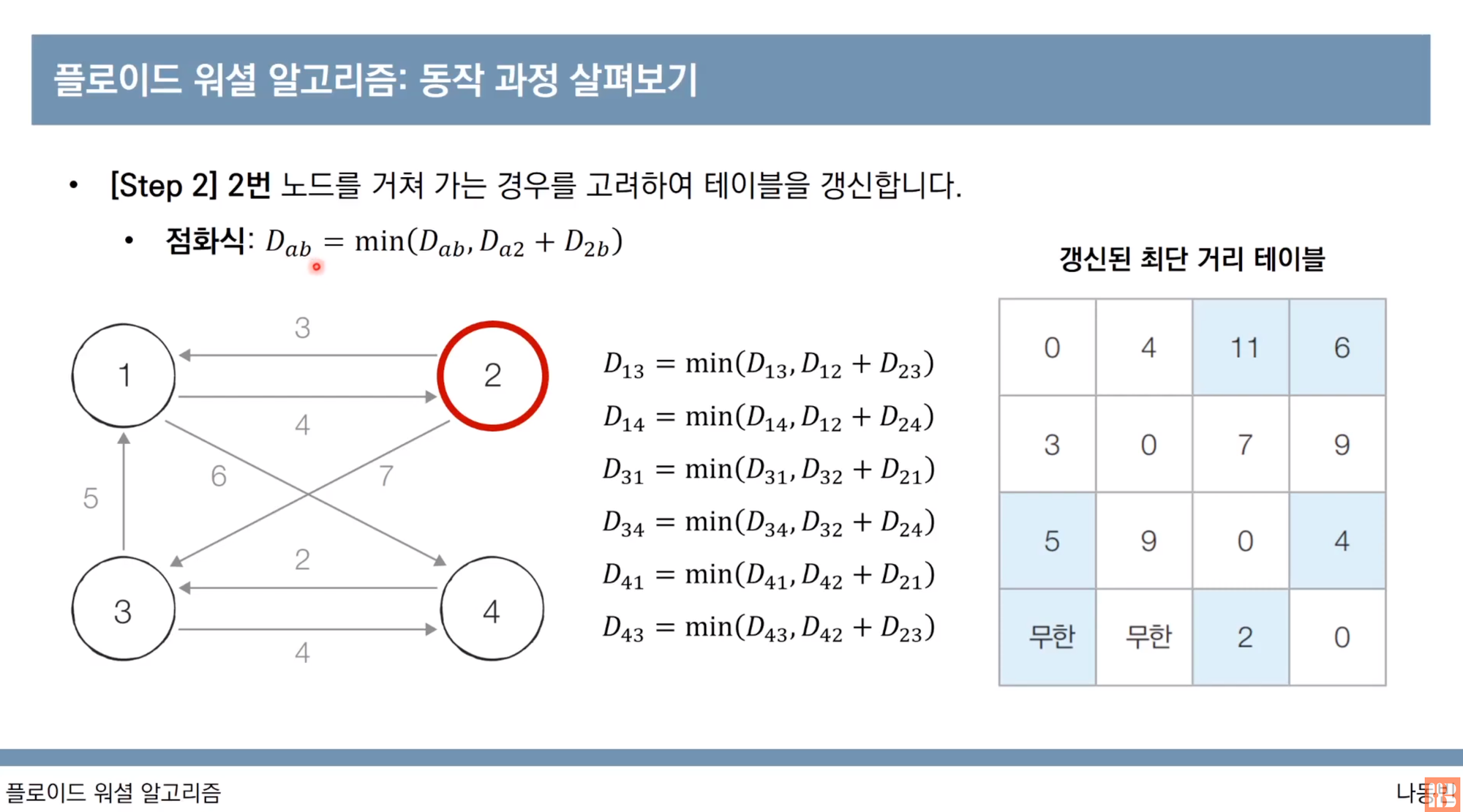
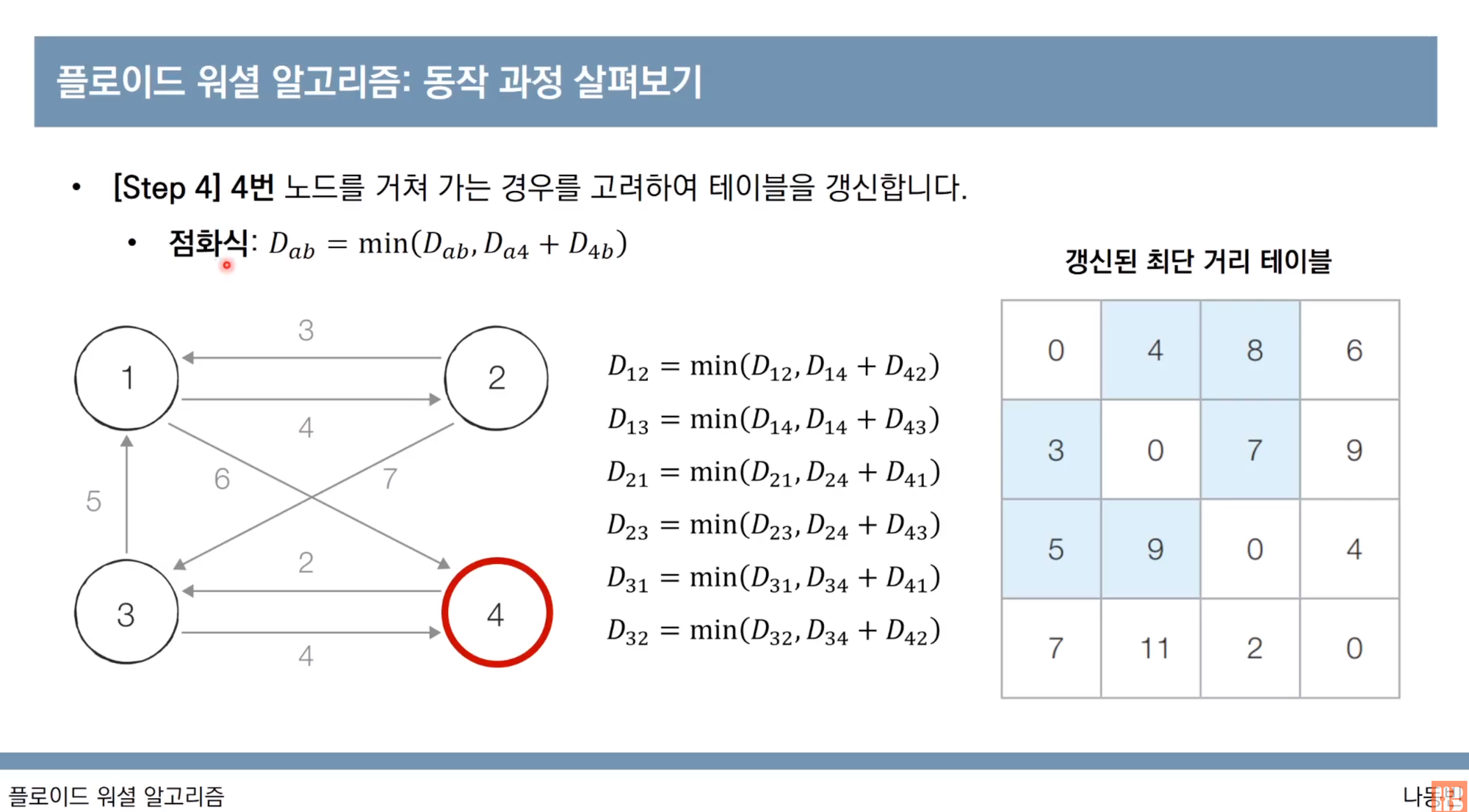
이렇게 2번 노드, 3번 노드, 4번노드도 똑같이 행렬 업데이트 과정을 진행하면 된다.
플로이드-워셜 알고리즘 성능
# 전체적인 과정
(for문) k번 노드를 거쳐 가는 과정
min(a → b, a → k → b)
# 여기에서 min(a → b, a → k → b)을 계산할 때 2차원 행렬이기 때문에 2중 반복문을 사용하게 됩니다.
# 풀어쓴 전체적인 과정
(for문) k번 노드를 거쳐 가는 과정
(for문) 행(row) 탐색
(for문) 열(column) 탐색
min(row -> column, row -> k -> column) 코드
n = int(input())
friends = [list(input()) for _ in range(n)]
#2차원 리스트(그래프)를 만들고 0으로 초기화
connected = [[0] * n for _ in range(n)]
#점화식에 따라 플로이드 워셜 알고리즘 수행
for k in range(n): #k를 거쳐가는 경우
for i in range(n):
for j in range(n):
if i == j:
continue
if friends[i][j] == "Y" or (friends[i][k] == "Y" and friends[k][j] == "Y"):
connected[i][j] = 1
#결과 계산
answer = 0
for row in connected:
answer = max(answer, sum(row))
print(answer)테스트케이스(예제 1) 검증
3
NYY
YNY
YYNconnected
[[0, 1, 0],
[1, 0, 1],
[1, 1, 0]]answer = sum(row) = 2

