Graph
정의
A graph, in the context of mathematics and computer science, is a data structure used to represent relationships between entities. It consists of two sets:
그래프는 수학과 컴퓨터 과학의 맥락에서 엔터티 간의 관계를 나타내는 데 사용되는 데이터 구조이다. 두 세트로 구성된다.
- Vertices 정점(V): Represent the entities themselves, also called nodes or points. 엔티티 자체를 나타내며 노드나 점이라고 한다.
Edges 모서리(E): Represent the relationships between the entities, also called links or lines. 링크나 선이라고도 하는 엔티티 간의 관계를 나타난다.
A graph is denoted as G = (V, E), where:
-V is a set of vertices.
-E is a set of edges.
그래프는 G = (V, E)로 표시되며, 여기서
-V는 정점의 집합입니다.
-E는 모서리의 집합입니다.
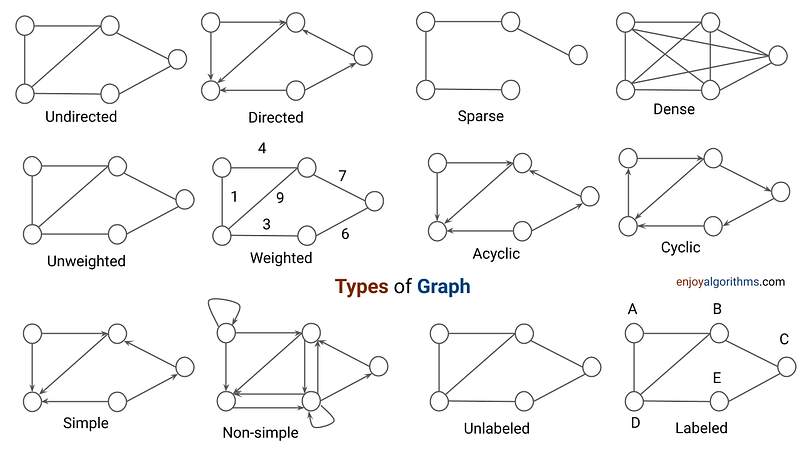
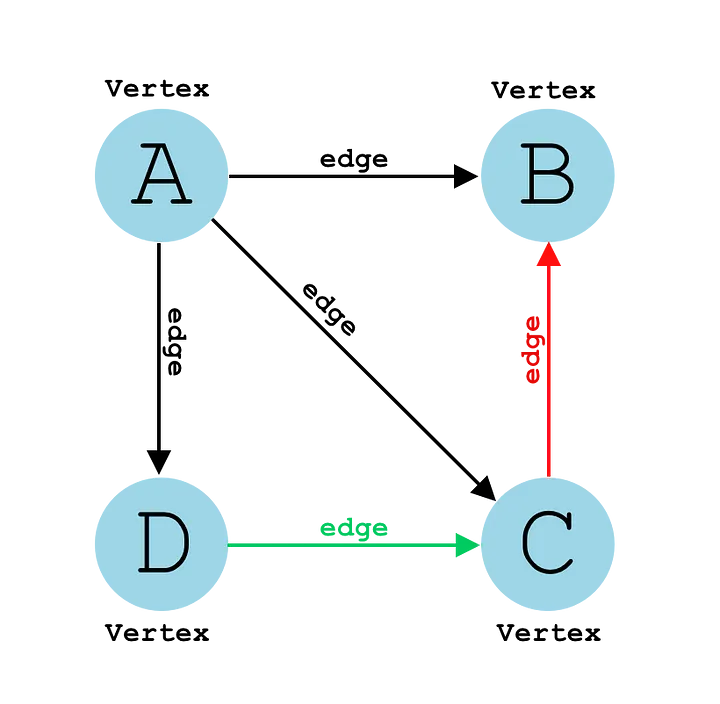
These edges can be directed or undirected:
이러한 모서리는 방향이 있거나 없을 수 있습니다.
- Directed edges: Have an arrow indicating direction, showing how one vertex connects to another (e.g., A → B).
방향이 있는 모서리: 방향을 나타내는 화살표가 있어 한 정점이 다른 정점에 연결되는 방식을 보여줍니다(예: A → B ). - Undirected edges: Have no direction, representing a bi-directional connection between two vertices (e.g., A - B).
무향 에지: 방향이 없으며 두 정점 사이의 양방향 연결을 나타냅니다(예: A - B ).
Graph Terminology
Graph: A collection of nodes (or vertices) and edges that connect pairs of nodes.
Vertex (Node): The fundamental unit by which graphs are formed. A vertex represents a point in the graph.
Edge: A line connecting two vertices in a graph. It can be directed (having a direction) or undirected (no direction).
Directed Graph (Digraph): A graph in which the edges have a direction, indicating a one-way relationship between vertices.
Undirected Graph: A graph in which the edges do not have a direction, indicating a two-way relationship.
Weighted Graph: A graph in which edges have weights assigned to them, typically representing costs, lengths, or capacities.
Unweighted Graph: A graph in which edges do not have weights.
Adjacent (Neighbors): Two vertices are adjacent if there is an edge connecting them.
Degree: The degree of a vertex is the number of edges connected to it. For directed graphs, there are in-degree (edges coming into the vertex) and out-degree (edges going out from the vertex).
Path: A sequence of edges that allows you to go from one vertex to another.
Cycle: A path that starts and ends at the same vertex without traversing any edge more than once.
Loop: An edge that connects a vertex to itself.
Subgraph: A graph formed from a subset of the vertices and edges of another graph.
Connected Graph: An undirected graph is connected if there is a path between every pair of vertices.
Disconnected Graph: A graph is disconnected if it is not connected, i.e., if there are at least two vertices with no path between them.
Complete Graph: A graph in which there is an edge between every pair of vertices.
Bipartite Graph: A graph whose vertices can be divided into two disjoint sets such that every edge connects a vertex in one set to a vertex in the other set.
Tree: A connected, undirected graph with no cycles.
Acyclic Graph: A graph with no cycles. In the context of directed graphs, it is often called a Directed Acyclic Graph (DAG).
Graph Isomorphism: Two graphs are isomorphic if there is a one-to-one correspondence between their vertex sets that preserves edge connectivity.
그래프: 노드(또는 정점)와 노드 쌍을 연결하는 모서리의 집합입니다.
정점(노드): 그래프가 형성되는 기본 단위. 정점은 그래프의 한 지점을 나타냅니다.
에지: 그래프에서 두 정점을 연결하는 선. 방향이 있거나(방향이 있음) 방향이 없을 수 있습니다.
유향 그래프(Digraph): 간선에 방향이 있는 그래프로, 정점 간의 단방향 관계를 나타냅니다.
무향 그래프: 간선에 방향이 없고 양방향 관계를 나타내는 그래프입니다.
가중치 그래프: 각 모서리에 가중치가 할당되어 있는 그래프로, 일반적으로 비용, 길이 또는 용량을 나타냅니다.
가중치가 없는 그래프: 모서리에 가중치가 없는 그래프입니다.
인접(이웃): 두 정점은 두 정점을 연결하는 변이 있는 경우 인접합니다.
차수: 정점의 차수는 정점에 연결된 에지의 수입니다. 방향 그래프의 경우, 인-차수 (정점에 들어오는 에지)와 아웃-차수 (정점에서 나가는 에지)가 있습니다.
경로: 한 정점에서 다른 정점으로 갈 수 있게 해주는 일련의 모서리.
사이클: 같은 정점에서 시작해서 끝나며, 어떤 모서리도 두 번 이상 통과하지 않는 경로.
루프: 정점을 자기 자신과 연결하는 모서리.
부분 그래프: 다른 그래프의 정점과 간선의 하위 집합으로 형성된 그래프입니다.
연결 그래프: 무향 그래프는 모든 정점 쌍 사이에 경로가 있는 경우 연결되었다고 합니다.
연결되지 않은 그래프: 그래프가 연결되지 않은 경우, 즉 두 개 이상의 정점 사이에 경로가 없는 경우 그래프가 연결되지 않은 것입니다.
완전 그래프: 모든 정점 쌍 사이에 간선이 존재하는 그래프입니다.
이분 그래프: 정점이 두 개의 분리된 집합으로 나뉘고, 모든 모서리가 한 집합의 정점을 다른 집합의 정점에 연결하는 그래프입니다.
트리: 사이클이 없고, 연결되고 방향이 없는 그래프입니다.
비순환 그래프: 사이클이 없는 그래프. 유향 그래프의 맥락에서 종종 유향 비순환 그래프(DAG)라고 불립니다.
그래프 동형성: 두 그래프는 정점 집합 간에 일대일 대응이 있고 모서리 연결성이 보존되는 경우 동형입니다.
Graph는 노드와 연결선으로 구성되어 있다.
Node가 있고 Edge로 다음을 연결하는 구조이다.
Graph는 한쪽방향으로만 연결 할 수도 있지만, 양방향으로도 연결할 수 있다. (양방향은 상,하 관계가 없다)
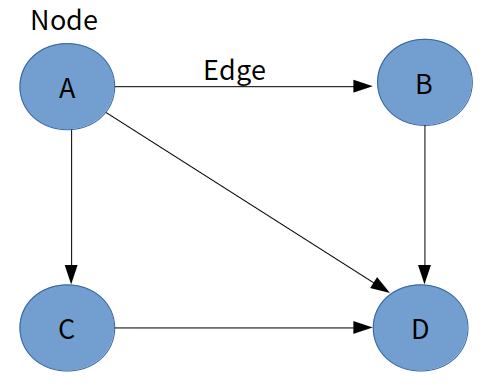
예를 들면, 현실에서는 주로 지하철 노선을 찾을 때, 많이 사용이 된다. 지금 있는 위치를 A라고 한다면, Node로 지정이 되고 D가 목적지라면 가는 방법은 분명 다양할 것이다. A-B-D로 갈수 도 있고, A-C-D로 갈수 있다. 이와 같이 Graph는 길을 찾을 때 많이 사용된다.
Node가 있으면, 다음 노드를 Edge로 연결해서 다음 값을 가르쳐 줘야한다. 방향이 있는 구조라면 하기 내용에 있는 Tree와 비슷하겠지만, 방향이 없다면 graph만의 특징을 갖는다. (상,하 구조 X)
JavaScript 그래프 알고리즘을 구현할 때는 다음과 같은 사항을 고려할 수 있다.
그래프는 인접 행렬 또는 인접 리스트로 표현할 수 있다.
인접 리스트를 사용하는 것이 더 효율적인 경우가 많습니다. 이는 메모리 사용량이 적고 검색 알고리즘을 수행할 때 시간 복잡도가 더 좋기 때문이다.
그래프를 사용하기 전에 명명법과 그래프 속성을 명확히 정의하는 것이 좋다.
js-graph-algorithms 패키지도 JavaScript 그래프 알고리즘을 구현한 패키지이다.
[Graph 알고리즘 예시]
- 미로 탐색
- 불리언 행렬 칠하기
- 둘러싸인 영역 계산
- 유향 그래프의 사이클 탐지(데드락 탐지)
- 그래프 복제
- 와이어드 연결 만들기
알고리즘 링크 : https://studyglance.in/ds/display.php?tno=32&topic=Introduction-to-Graph
