수학 1 (연습)

9613번 GCD 합

문제

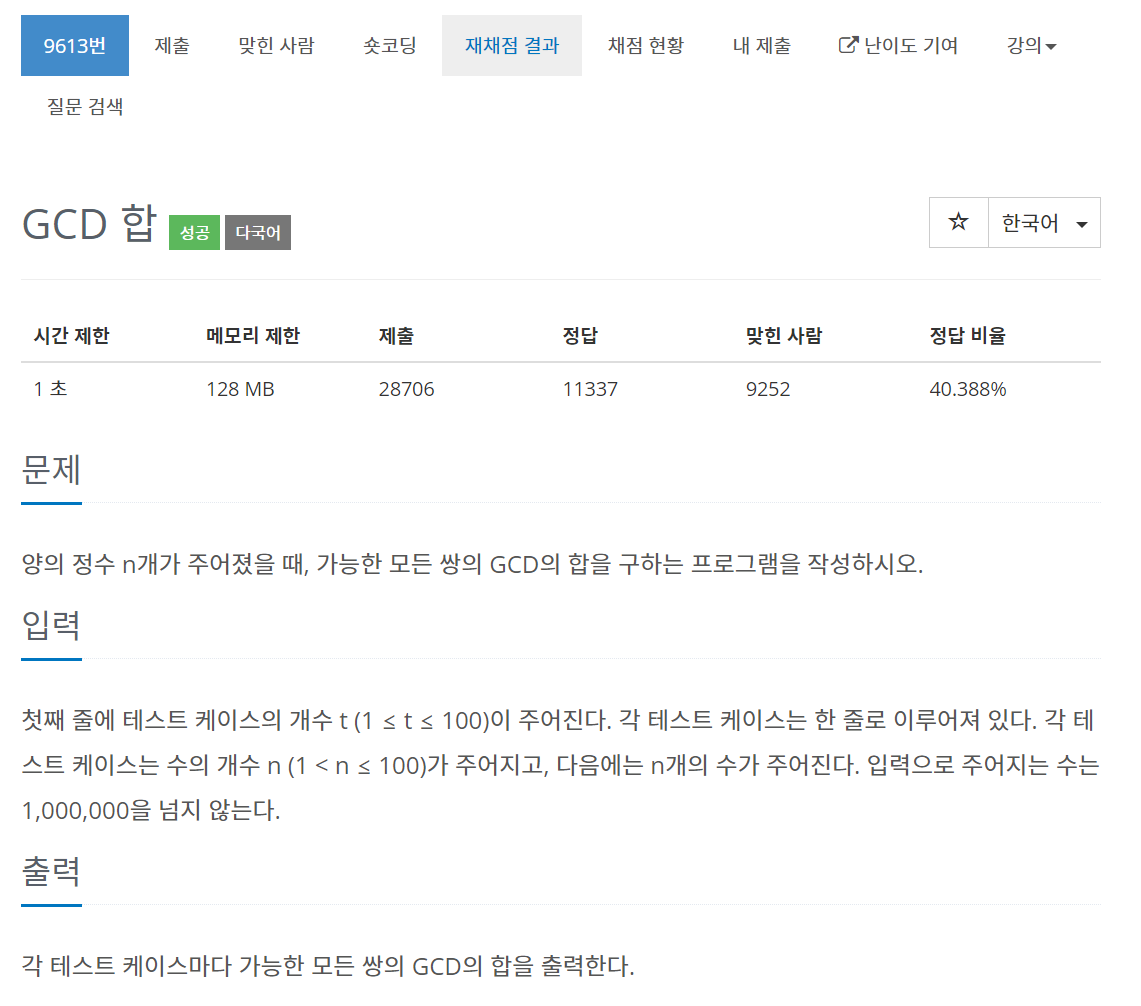
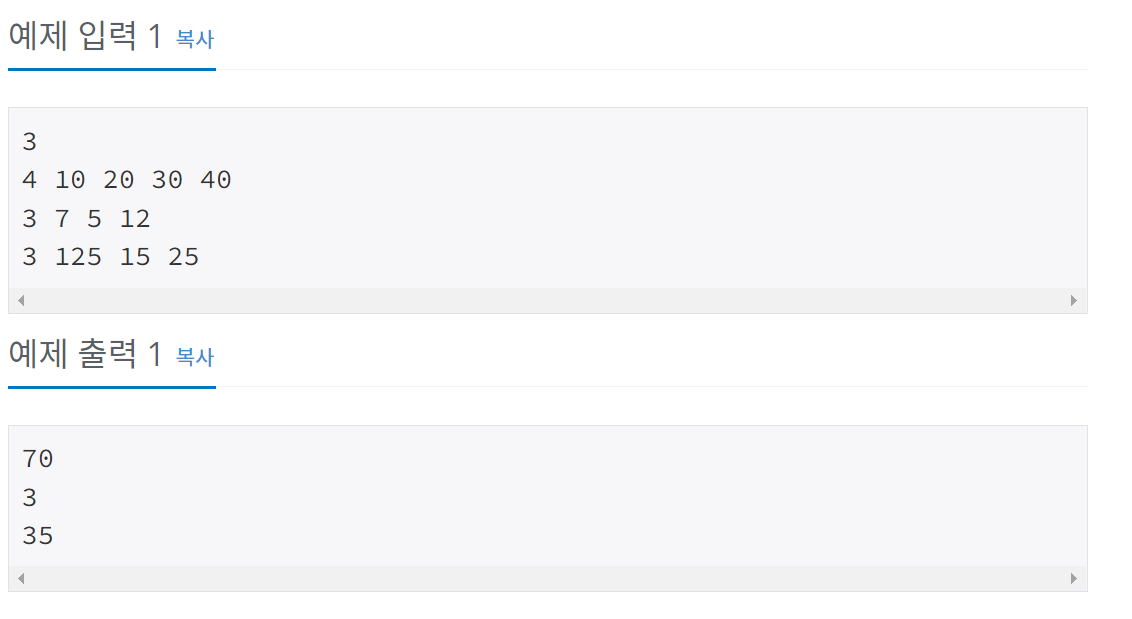
풀이

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();

        for (int i = 0; i < n; i++) {
            int a = sc.nextInt();
            int arr[] = new int[a];
            for (int j = 0; j < a; j++) {
                arr[j] = sc.nextInt();
            }
            long sum = 0;
            // 1, 2 / 2, 3 / 3, 4 이런 형태의 매개변수로 gcd 호출
            for (int k = 0; k < a - 1; k++) {
                for (int m = k + 1; m < a; m++) {
                    sum += gcd(arr[k], arr[m]);
                }
            }
            System.out.println(sum);
        }

        sc.close();
    }

    // 유클리드 호제법 이용
    static int gcd (int a, int b) {
        if(b == 0) {
            return a;
        } else {
            return gcd(b, a % b);
        }
    }
}

17087번 숨바꼭질 6

문제

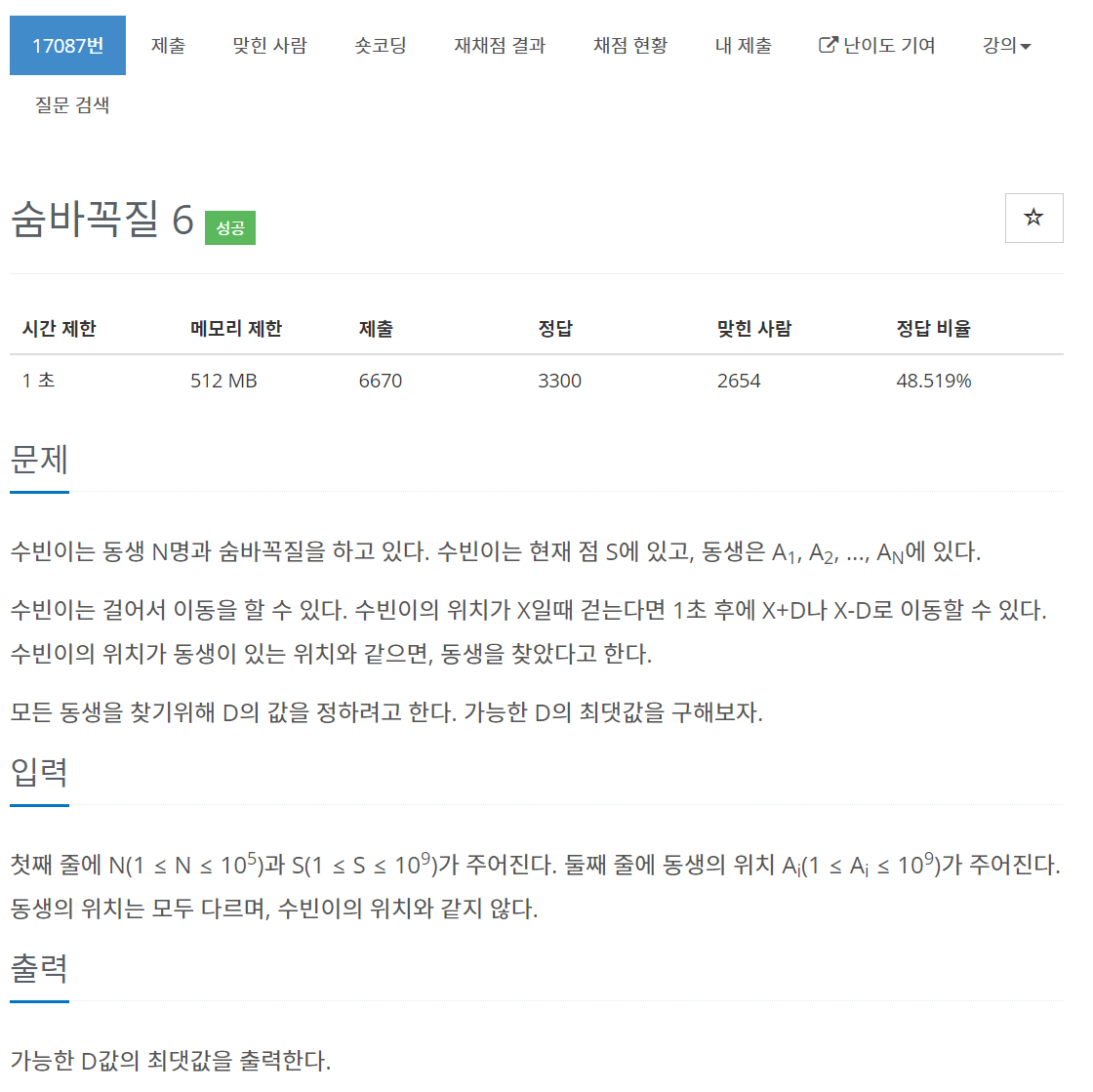
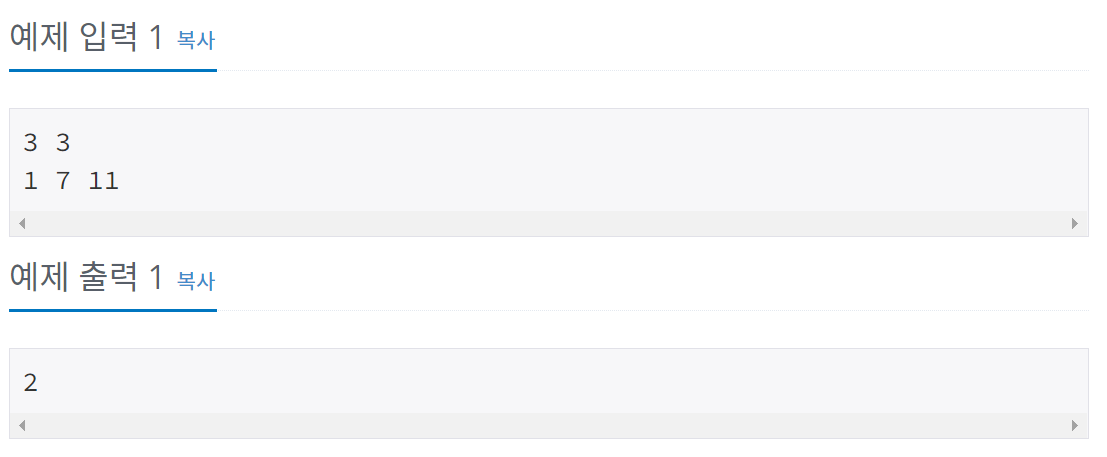
풀이

-> 최대공약수를 구하는 문제이다.

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        int a = sc.nextInt();
        int b = sc.nextInt();
        int arr[] = new int[a];

        for(int i = 0; i < a; i++) {
            int n = sc.nextInt(); // 동생 위치
            arr[i] = Math.abs(b - n); // 나의 위치와 동생의 위치 차이
        }

        int answer = arr[0];
        for(int i = 1; i < arr.length; i++) {
            answer = gcd(answer, arr[i]); // 위치 차이들 중에서 최대공약수 구하기
        }
        System.out.println(answer);

        sc.close();
    }

    // 유클리드 호제법 이용
    static int gcd (int a, int b) {
        if(b == 0) {
            return a;
        } else {
            return gcd(b, a % b);
        }
    }
}

2089번 -2진수

문제

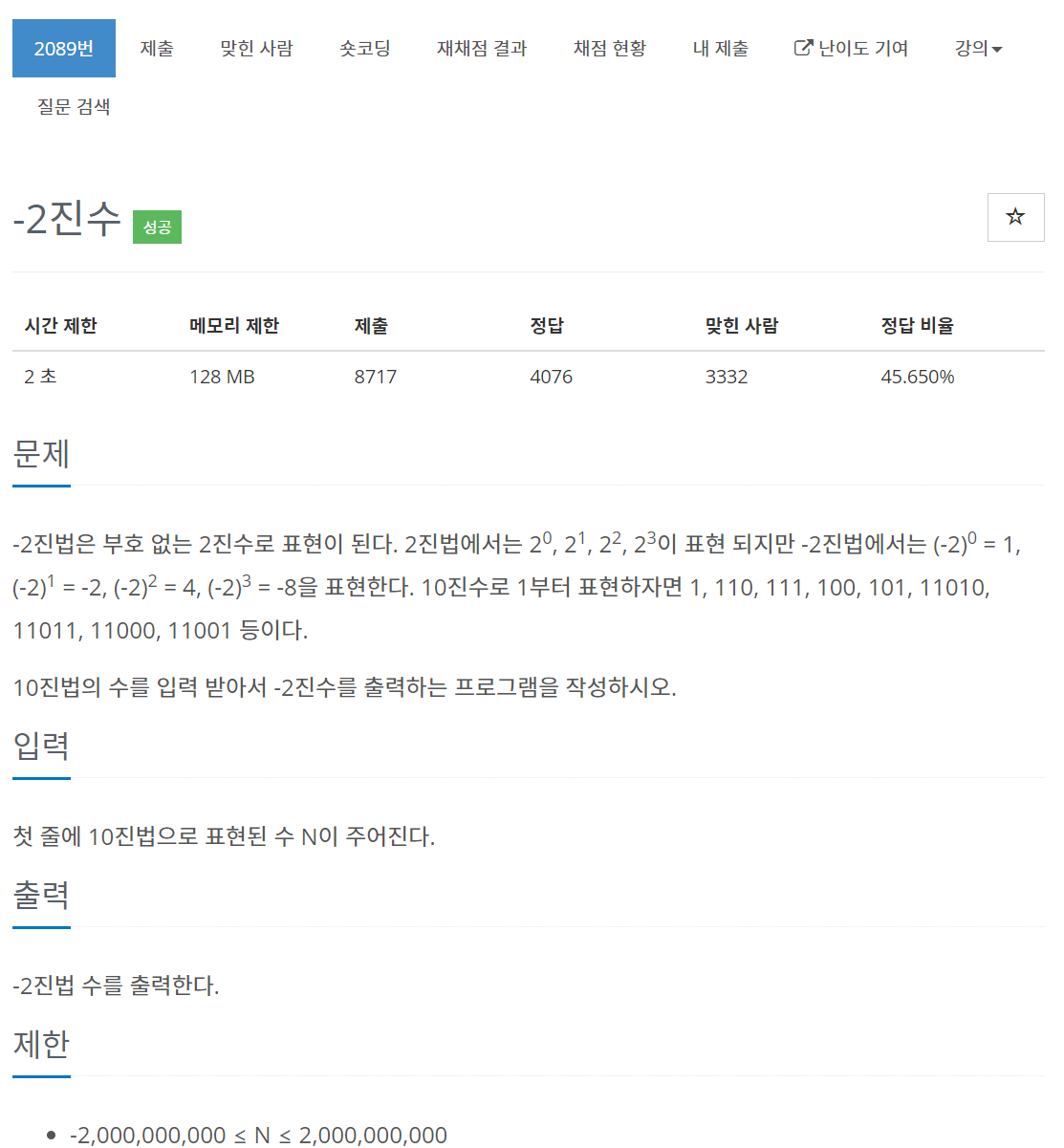
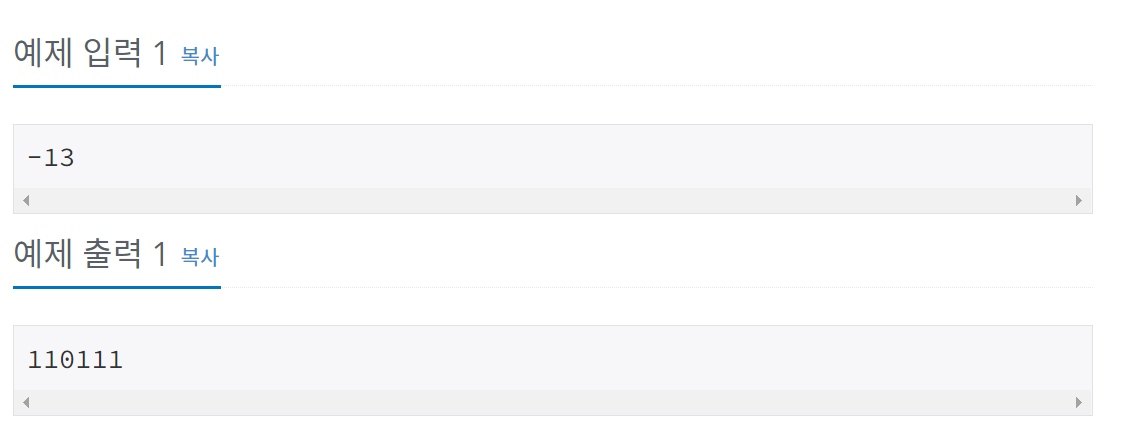
풀이

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        StringBuilder sb = new StringBuilder();
        
        int n = sc.nextInt();
        
        if(n == 0) {
            System.out.println(0);
        } else {
            while(n != 1) {
                sb.append(Math.abs(n % -2));
                n = (int)Math.ceil((double)n / (-2));
            }
            sb.append(n);
        }
        System.out.println(sb.reverse());
        
        sc.close();
    }
}