[js] 겹치는 선분의 길이

선분 3개가 평행하게 놓여 있습니다. 세 선분의 시작과 끝 좌표가 [[start, end], [start, end], [start, end]] 형태로 들어있는 2차원 배열 lines가 매개변수로 주어질 때, 두 개 이상의 선분이 겹치는 부분의 길이를 return 하도록 solution 함수를 완성해보세요.

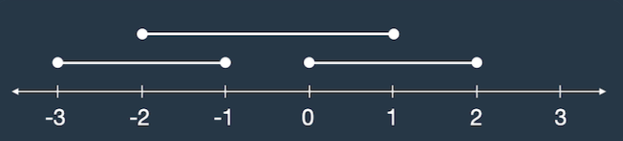
lines가 [[0, 2], [-3, -1], [-2, 1]]일 때 그림으로 나타내면 다음과 같습니다.

선분이 두 개 이상 겹친 곳은 [-2, -1], [0, 1]로 길이 2만큼 겹쳐있습니다.

제한사항

• lines의 길이 = 3
• lines의 원소의 길이 = 2
• 모든 선분은 길이가 1 이상입니다.
• lines의 원소는 [a, b] 형태이며, a, b는 각각 선분의 양 끝점 입니다.
  - -100 ≤ a < b ≤ 100
  

나의 풀이

function solution(lines) {
    const answer = 0;
    
    for (let i=-100; i<100; i++) {
        let count = 0;
        if (lines[0][0] <= i && lines[0][1] > i) count++;
        if (lines[1][0] <= i && lines[1][1] > i) count++;
        if (lines[2][0] <= i && lines[2][1] > i) count++;
        
        if(count > 1) answer++;
    }
    return answer;
}

와 이건... 진짜 너무 어려웠다... 좌표랑 선분 이런거 나오면 진짜 죽겠음 제발 ㅠㅠ 사실 못 풀어서 남친이랑 같이 풀고 날 이해시켜달라고 당당하게 나왔음 하지만 아직도 혼자 풀라고 하면 못 풀 것 같음 젠장

1. 결과를 저장할 변수 answer을 0으로 초기화한다.
2. 선분들의 범위를 고려하여 -100부터 99까지의 모든 정수 값을 순회한다.
3. 각 정수값 i에 대해 겹치는 선분의 개수를 세기 위한 변수 count를 0으로 초기화한다.
   • if (lines[0][0] <= i && lines[0][1] > i) count++; : 첫 번째 선분의 시작점이 i이하이고 끝점이 i를 초과하는 경우 count를 1 증가시킨다.
   • if (lines[1][0] <= i && lines[1][1] > i) count++; : 두 번째 선분의 시작점이 i이하이고 끝 점이 i를 초과하는 경우 count를 1 증가시킨다.
   • if (lines[2][0] <= i && lines[2][1] > i) count++; : 세 번째 선분의 시작점이 i이하이고 끝점이 i를 초과하는 경우 count를 1 증가시킨다.
   • ➡️ 이렇게 되면 선분이 최소한 하나라도 지나가는 경우 count에 값이 들어온다. 선분이 지나가는 곳만 체크하게 코드를 짠 것...
4. if(count > 1) answer++; : 특정 정수 i에 대해서 1보다 크다는 의미는 겹치는 선분이라는 뜻이다. 겹치는 선분의 개수가 2개 이상인 경우에 answer를 1증가시킨다. 이를 통해서 겹치는 값 i를 구할 수 있다.
   • count가 1이면 선분이 하나만 지나가는 것이고, 2라면 선분이 두 개, 3이라면 선분이 3개 지나가는 i임을 알 수 있다. 이를 통해서 겹치는 선분의 길이만 구할 수 있다.
5. 최종적으로 계산된 answer를 반환한다.

솔직히 이것이 그렇게 효율적인 코드인지는 잘 모르겠다. 왜냐면... i가 커지면 커질 수록 순환을 미친듯이 돌아야 하기 때문이다. 하지만 어떻게 푸는지 조차 이해가 안갔던 나 ^^,,, 겨우 좀 이해가 갈 것 같긴 한데 설명하는 건 언제나 어렵다.

다른 풀이 1

function solution(lines) {
    let line = new Array(200).fill(0);

    lines.forEach(([a, b]) => {
        for(; a < b; a++) line[a+100]++;
    });

    return line.reduce((a, c) =>  c > 1 ? a + 1 : a, 0)
}

1. 선분의 범위를 고려하여 길이가 200인 배열 line을 생성하고 모든 요소를 0으로 초기화한다.
2. foreEach() 메서드를 통해 입력으로 주어진 선분 정보 lines를 순회한다. a는 선분의 시작 좌표, b는 선분의 끝 좌표이다.
3. for(; a < b; a++) line[a+100]++;
   • 각 선분의 시작 좌표부터 끝 좌표까지 반복문을 실행한다.
   • 반복문 내부에서는 line[a+100]++ 연산이 수행된다. a+100은 배열의 인덱스를 계산하는 부분이다.
     ➡️ 좌표는 -100부터 시작이지만 우리가 line이라는 배열을 만들었을 때는 마이너스 인덱스를 만들 수 없기 때문에 +100을 통해서 음수를 양수로 바꿔주는 것이다.
   • 또한 line[a+100]++에서 ++는 해당 인덱스의 값을 1 증가시키는 연산이다. 이를 통해서 각 좌표에서 겹치는 선분의 개수를 기록할 수 있다.
     ➡️ 0으로 초기화했던 인덱스의 값을 1씩 증가시키기 때문에! 위에서 풀었던 풀이와 비슷함.
4. lines 배열을 reduce() 메서드를 통해서 순회한다. 현재 값이 1 초과라는 것은 겹치는 선분이 존재한다는 뜻이기 때문에 a+1을 해주고, 아니라면 a를 그대로 둔다.최종적으로 겹치는 선분의 길이를 모두 합한 a값을 반환한다.

와... 이렇게 또 풀어봐야 하는데... 머리로 구조화하는 것이 진짜 어렵다. 어려워서 뤼튼한테 물어봄. 나중에 또 보면 이해 못할 것 같으니까 사진 첨부해둠.

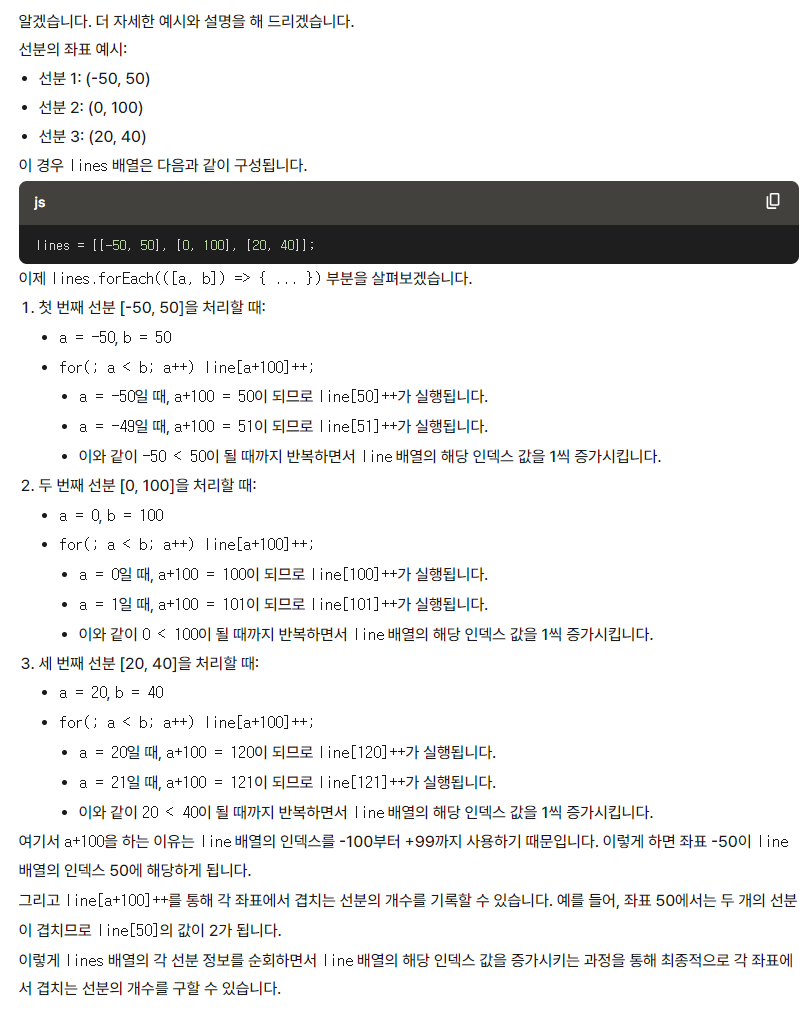
이해가 안 가서 한 세 번은 다시 물어봤다 ㅋㅋㅋㅋ

다른 풀이 2

function solution(lines) {
    var min = Math.min(...lines.flat());
    var max = Math.max(...lines.flat());
    var totalOverlappedLength = 0;

    function isInbound(x, [a,b]){

        var s = Math.min(a,b);
        var e = Math.max(a,b);

        x = x + 0.5;

        if ((s < x)&&(x < e)){
            return true;
        }
        return false;
    }

    for(let x = min; x < max; x++){
        var overlappedOnX = 0;
        lines.forEach((el) => {
            if(isInbound(x,el)){
                overlappedOnX = overlappedOnX + 1;
            }
        });

        if(overlappedOnX > 1){
            totalOverlappedLength = totalOverlappedLength + 1;
        }
    }

    return totalOverlappedLength;
}

1. min과 max는 각각 lines 배열에 있는 모든 좌표 중 가장 작은 값과 큰 값을 구한다.
2. totalOverlappedLength는 겹치는 선분의 총 길이를 저장할 변수이다.
3. isInbound(x, [a, b]) 함수는 주어진 좌표 x가 선분 [a, b]안에 포함되는지를 확인한다. x에 0.5를 더하는 것은 정수 좌표에서 겹치는 부분을 확인하기 위한 것이다.
4. for 루프를 통해서 min부터 max - 1까지 모든 정수 좌표 x를 확인한다.
5. 각 좌표 x에 대해서 lines 배열의 모든 선분을 확인하고 해당 좌표가 선분 안에 포함되는지 isInbound함수로 확인한다.
6. overlappedOnX > 1 : 선분이 겹치는 경우 totalOverlappedLength를 1 증가시킨다.
7. 마지막으로 반환한다.