2D Homography

Henry·2023년 4월 10일
3D VisionDLHomographyML딥러닝선형변환
1

3D Vision

목록 보기
1/3

왜 2D Homography가 중요한가?

2020년 ECCV에 발표된 NeRF(Neural Radiance Fields)를 기점으로 3D vision 분야는 어마어마한 주목을 받았다.

3D vision의 여러 연구를 살펴보면서 느낀 것은 카메라, 좌표계, 그리고 전통적인 그래픽스 내용들에 대한 이해가 정말 중요하다는 사실이었다.

또한 회사를 다녀보면서 raw data로부터 3D vision model을 만들기까지 얼마나 많은 수학적인 내용들이 필요한지 뼈저리게 체험할 수 있었다.

3D 상의 image들의 변환과 좌표계를 이해하기 위해 2D Homography를 이해하는 것은 필수적이다.

과거의 나처럼 3D vision 공부를 처음 시작하는 이에게 도움이 되고자 포스트를 써본다.

2D Homography

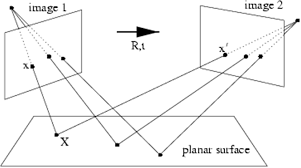
2D Homography (Projective Transformation)는 점 x,y,zx, y, z와 점 h(x),h(y),h(z)h(x), h(y), h(z)가 iffiff 각자 하나의 line 위에 놓여있는 때, P2\mathbb{P}^2에서 자기 자신으로의 invertible mapping hh를 의미한다.

쉽게 말해 두 이미지의 매칭 관계, 즉 한 쪽에서 바라본 2차원의 이미지를 다른 한 쪽에서 바라볼 때로 전환하는 변환을 모델링 할 때 사용하는 방법이다.

이는 한 쪽 좌표가 다른 좌표의 선형 변환임을 두고 풀 수 있다.

x′=Hxx'=Hx
(x1′x2′x3′)=[h11h12h13h21h22h23h31h32h33](x1x2x3)\begin{pmatrix} x^{'}_{1} \\ x^{'}_{2} \\ x^{'}_{3} \\ \end{pmatrix} = \begin{bmatrix} h_{11} & h_{12} & h_{13}\\ h_{21} & h_{22} & h_{23}\\ h_{31} & h_{32} & h_{33}\\ \end{bmatrix} \begin{pmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{pmatrix}

위와 같이 matrix로 나타내었지만 이미지는 2차원 좌표이므로 zz축을 나타내는 x3′x^{'}_{3}과 x3x_{3}은 1이다.
그러면 마지막 x3x_{3}를 1로 만들기 위해 HH matrix는 나눗셈을 해줘야하고 이 나눗셈은 9개의 변수가 서로 연관이 되어버리게 만들어 HH matrix가 9개가 아닌 8개의 자유도를 갖게 된다.

(x1′x2′x3′)=[h11′h12′h13′h21′h22′h23′h31′h32′1](x1x2x3)\begin{pmatrix} x^{'}_{1} \\ x^{'}_{2} \\ x^{'}_{3} \\ \end{pmatrix} = \begin{bmatrix} h^{'}_{11} & h^{'}_{12} & h^{'}_{13}\\ h^{'}_{21} & h^{'}_{22} & h^{'}_{23}\\ h^{'}_{31} & h^{'}_{32} & 1\\ \end{bmatrix} \begin{pmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{pmatrix}

따라서 2D Homography (Projective Transformation)은 8 df (degrees of freedom)8 \space df \space (degrees \space of \space freedom)을 갖는다.

이외에도 더 다양한 변환들이 있다.

Translation

앞선 8자유도의 변환 외에도 제약을 가한 변환들이 많다. 하나씩 살펴보자.
Translation은 평행이동만을 하는 변환이다.

(x1′x2′x3′)=[10tx01ty001](x1x2x3)\begin{pmatrix} x^{'}_{1} \\ x^{'}_{2} \\ x^{'}_{3} \\ \end{pmatrix} = \begin{bmatrix} 1 & 0 & tx\\ 0 & 1 & ty\\ 0 & 0 & 1\\ \end{bmatrix} \begin{pmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{pmatrix}

이를 풀어쓰면 다음과 같고

x1′=x1+txx2′=x2+tyx^{'}_{1} = x_1 + tx \\ x^{'}_{2} = x_2 + ty

txtx와 tyty에 의해 결정되므로 dfdf는 2이다.
이때 txtx는 tt와 xx의 곱이 아닌 하나의 변수이니 오해말자.

Euclidean Transformation

Euclidean Transformation은 회전(rotation)과 변환(translation)이 가능한 변환으로 강체 변환(Rigid Transformation)이라고도 부른다.

(x1′x2′x3′)=[cos(t)−sin(t)txsin(t)cos(t)ty001](x1x2x3)\begin{pmatrix} x^{'}_{1} \\ x^{'}_{2} \\ x^{'}_{3} \\ \end{pmatrix} = \begin{bmatrix} cos(t) & -sin(t) & tx\\ sin(t) & cos(t) & ty\\ 0 & 0 & 1\\ \end{bmatrix} \begin{pmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{pmatrix}

이는 아래와 같은 회전 변환 matrix에 translation을 결합한 것이다.

[cos(t)−sin(t)sin(t)cos(t)]\begin{bmatrix} cos(t) & -sin(t)\\ sin(t) & cos(t)\\ \end{bmatrix}

coscos과 sinsin의 각도를 결정하는 tt와 txtx 그리고 tyty에 의해서 결정되므로 3 dfdf이다.

Similarity Transformation

Similarity Transformation은 Euclidean Transformation에 scaling을 추가한 것이다.

(x1′x2′x3′)=[s∗cos(t)−s∗sin(t)txs∗sin(t)s∗cos(t)ty001](x1x2x3)\begin{pmatrix} x^{'}_{1} \\ x^{'}_{2} \\ x^{'}_{3} \\ \end{pmatrix} = \begin{bmatrix} s*cos(t) & -s*sin(t) & tx\\ s*sin(t) & s*cos(t) & ty\\ 0 & 0 & 1\\ \end{bmatrix} \begin{pmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{pmatrix}

ss라는 scaling factor가 추가되었으므로 4 dfdf를 갖는다.

Affine Transformation

(x1′x2′x3′)=[abcdef001](x1x2x3)\begin{pmatrix} x^{'}_{1} \\ x^{'}_{2} \\ x^{'}_{3} \\ \end{pmatrix} = \begin{bmatrix} a & b & c\\ d & e & f\\ 0 & 0 & 1\\ \end{bmatrix} \begin{pmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{pmatrix}

Affine Transformation은 x3x_3를 이미 1로 만들고 있으므로 a~f만 변환에 영향을 끼친다. 따라서 6 dfdf를 갖는다.

Affine Transformation과 Similarity Transformation의 차이는 무엇일까?

많은 사람들이 Affine Transformation과 Similarity Transformation을 헷갈려한다.

Similarity Transformation은 회전과 변환 그리고 스케일링만 갖는다면 Affine Transformation은 그 외의 변환(e.g. reflection)도 나타날 수 있다.

여기서 그 외의 변환이라함은 3차원에서 물리적으로 일어날 수 없는 변환들을 의미한다.

따라서 이러한 관점으로 봤을 때, 6자유도의 변환인 Affine Transformation이나 8자유도를 갖는 Projective Transformation은 현실 세계에서 존재하지 않는 변환들이 모델링 될 수 있다.

그렇다고 두 변환이 의미 없는 것은 아니며, 다만 선형 변환의 해를 구하여 사용 할 때 불가능한 변환을 제거 후 사용해야한다.

Case of Impossible Transformation

현실 세계에서 일어날 수 없는 변환들에 대해 다시 한번 알아보자.

Affine Transformation

6 dfdf를 갖는 Affine Transforamtion에서는 뒤집힘(reflection)이 발생하게 된다.

reflection은 언뜻 보기에 물리적으로 일어날 수 있어보이지만 pattern matching 관점에서 일어날 수 없는 변환이다.

2D Homography

8 dfdf를 갖는 2D Homography, Projective Transformation에서는 reflection뿐만 아니라 뒤틀림(twist)과 오목(concave) 현상 또한 나타난다. 이는 2D Homography가 Affine Transformation보다 더 많은 자유도를 갖고 있기 때문이다.

How to Find the Homography

그렇다면 어떻게 HH를 구할까? 선형 변환 HH를 구하는 방법은 여러 가지가 있을 수 있다. 대표적인 방법인 DLT (Direct Linear Transformation)에 대해 알아보자.

Direct Linear Transformation

HH를 찾는 방법인 DLT의 수식 전개를 살펴보기 전에 다음과 같은 사실에 대해 remind하자.

  1. 우리는 homogenous system에서 논의하고 있으므로 scaling은 중요하지 않다.

  2. Let x=(x, y, z) and [x]x=(0z−y−z0xy−x0)x×xT=[x]xxTLet \space x = (x, \space y, \space z) \space and \space [x]_{x} = \begin{pmatrix} 0 & z & -y \\ -z & 0 & x \\ y & -x & 0 \end{pmatrix} \\ x \times x^T = [x]_xx^T

이 때, [x]x[x]_{x}는 외적곱 matrix이다.

다음으로, 교차하는 두 직선 lal_a와 lbl_b에 대해 교차점 xx는 x=la×lbx=l_a \times l_b 로 구할 수 있으며

두 점 pap_a와 pbp_b를 지나는 직선 ll은 l=pa×pbl = p_a \times p_b 로 구할 수 있다.

위와 같은 notation과 theorem에서

(x1′x2′x3′)=[h11h12h13h21h22h23h31h32h33](x1x2x3)⇒x′=Hx⇒x′×Hx=0⟺[x′]xHx=0\begin{pmatrix} x^{'}_{1} \\ x^{'}_{2} \\ x^{'}_{3} \\ \end{pmatrix} = \begin{bmatrix} h_{11} & h_{12} & h_{13}\\ h_{21} & h_{22} & h_{23}\\ h_{31} & h_{32} & h_{33}\\ \end{bmatrix} \begin{pmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{pmatrix} \Rightarrow x^{'} = Hx \Rightarrow x^{'} \times Hx = 0 \Longleftrightarrow [x^{'}]_{x}Hx = 0

[x1′x2′x3′]\begin{bmatrix} x^{'}_{1} \\ x^{'}_{2} \\ x^{'}_{3} \\ \end{bmatrix}를 [h1h2h3]\begin{bmatrix} h_1 & h_2 & h_3 \end{bmatrix}로 나타내고 [x′]x[x^{'}]_{x}를 풀어 쓰면 수식은 다음과 같다.

[x′]xHx=[x′]x[h1Txh2Txh3Tx]=[0T−x3′xTx2′xTx3′xT0T−x1′xT−x2′xTx1′xT0T][h1h2h3]=Q[h1h2h3]=0[x^{'}]_{x}Hx = [x^{'}]_{x} \begin{bmatrix} h_1^Tx \\ h_2^Tx \\ h_3^Tx \end{bmatrix} = \begin{bmatrix} 0^T & -x^{'}_{3}x^T & x^{'}_{2}x^T\\ x^{'}_{3}x^T & 0^T & -x^{'}_{1}x^T\\ -x^{'}_{2}x^T & x^{'}_{1}x^T & 0^T\\ \end{bmatrix} \begin{bmatrix} h_1 \\ h_2 \\ h_3 \end{bmatrix} = Q\begin{bmatrix} h_1 \\ h_2 \\ h_3 \end{bmatrix} = 0

이 때, QQ에서 첫번째 row에 x1′x^{'}_1을 곱하고 두번째 row에 x2′x^{'}_2를 곱한 후 이 둘을 더하고 scaling하여 세번째 row를 구할 수 있다.

이는 QQ가 linear combination임을 의미하며 따라서 QQ의 세번째 row는 지울 수 있다.

∴  [0T−x3′xTx2′xTx3′xT0T−x1′xT][h1h2h3]=Ah=0\therefore \space \space \begin{bmatrix} 0^T & -x^{'}_{3}x^T & x^{'}_{2}x^T\\ x^{'}_{3}x^T & 0^T & -x^{'}_{1}x^T \end{bmatrix} \begin{bmatrix} h_1 \\ h_2 \\ h_3 \end{bmatrix} = Ah = 0

위와 같은 form에서 hh의 해는 SVD (Singular Vector Decomposition)로 찾을 수 있다.

우선 Ah=0Ah = 0의 가장 쉬운 해는 h=0h=0이나 이 경우는 카메라를 무한히 먼 거리에 둔 것과 같은 의미이므로 trivial solution이다.

따라서 결과적으로 우리가 찾고자하는 hh는 가장 작은 singular value를 갖는 singular vector가 된다. 이 과정을 수학적으로 살펴보자.

Mathematics in DLT

두 카메라의 관계를 일정한 scale 범위 내에서 측정하는 것이 좋고, homogeneous system에서는 scaling이 상관없으므로 ∣∣h∣∣=1||h|| = 1와 같이 euclidean norm을 도입한다. 따라서 구해야할 해는 다음과 같다.

Ah=0where  ∣∣h∣∣=1Ah = 0 \\where \space\space ||h|| = 1

이러한 문제 상황은 Convex Optimization의 KKT condition을 만족하며, 이 조건에 따라 위 문제는 다음과 같이 라그랑지안으로 변형할 수 있다.

L=(Ah)−1(Ah)+λ(1−hTh)  \mathcal{L} = (Ah)^{-1}(Ah) + \lambda(1-h^Th) \space\space
∵(Ah)T(Ah)=0 and (hTh)12=1\because (Ah)^T(Ah)=0 \space and \space (h^Th)^{1 \over 2} = 1

이에 대한 라그랑지안의 derivative는 다음과 같다.

∇hL=2ATAh−2λh\nabla_h \mathcal{L} = 2A^TAh - 2 \lambda h
ATAh∗=λh∗A^TAh^* = \lambda h^*

이는 결국 singular value problem이므로 아래를 만족해야한다.

L(h∗)=λ\mathcal{L}(h^*) = \lambda

이 때 라그랑지안이 가장 작은 hh가 optimal solution인 h∗h^*가 되므로 h∗h^*는 singular value가 가장 작은 singular vector가 된다.

Problems of DLT

(1) DLT is not an optimal solution
DLT는 Algebraic solution이며 hh는 ∣∣Ah∣∣=∣∣x′×Hx∣∣||Ah|| = ||x^{'} \times Hx||를 만족한다.

그러나 우리가 해결해야할 문제 상황은 ∣∣x′−Hx∣∣||x^{'} - Hx||이다.

∣∣x′×Hx∣∣||x^{'} \times Hx|| 와 ∣∣x′−Hx∣∣||x^{'} - Hx|| 가 동일한 상황이라면 같은 solution이 될 수 있지만 실제 두 이미지의 연관에는 noise가 있으므로 두 상황이 동일하다고 보기 어렵다.

따라서 DLT를 통해 찾아낸 h∗h^*가 물리적으로 유의미하지 않은 결과일 수 있다.

그러나 이러한 부정확성에도 불구하고 DLT는 SVD를 통해 값을 얻어낸다는 점에서 수학적으로 잘 정의되어있고, 또한 SVD는 미분 가능한 operation이므로 DNN의 학습의 관점에서 DLT를 쓰는 것은 합리적이라고 볼 수 있다.

(2) Normalization issue
이미지는 2차원이므로 z축이 1인점을 고려한다면 AA matrix에서 어떠한 값은 작은 range를 갖고, 어떠한 값은 굉장히 큰 range를 갖게 된다.

즉, 0에 가까운 작은 수와 굉장히 큰 수가 하나의 matrix 안에 공존할 수 있는 것이다.

이러한 상황은 수학적으로 완벽한 수식이더라도 computation 관점에서 numerical precision 문제를 일으켜 noise가 많이 발생할 수 있다.

이는 (x, y)(x, \space y) 좌표계를 DLT에 넣기 전 0 ~ 1로 normalize 함으로써 해결할 수 있다.

(3) 2D is not ENOUGH
DLT와 그것의 장단점을 알고 개선함에도 불구하고 여전히 2D to 2D 상황에서는 3차원 현실의 물리법칙으로는 설명할 수 없는 transformation들이 발생한다. (e.g. shear transformation)

Conclusion

  1. 2D에서 2D로의 다양한 변환들이 존재한다.
  2. 일부 변환들은 3차원 현실에 존재하지 않는 변환들도 표현될 수 있으므로 조심해야한다.
  3. 문제의 특성에 맞게 변환을 선택해야한다.
  4. 그럼에도 불구하고 3차원을 거쳐가는 transformation이 필요하다.

References

https://darkpgmr.tistory.com/79
https://en.wikipedia.org/wiki/Homography
https://www.cs.umd.edu/class/spring2020/cmsc426-0201/files/18_Homography-estimation-and-decomposition.pdf

profile
Henry
Intern of Arcreal
다음 포스트

Pinhole Camera & Camera Calibration

0개의 댓글