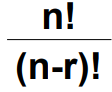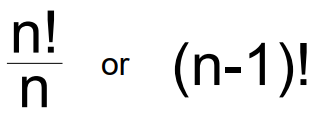기초수학 2

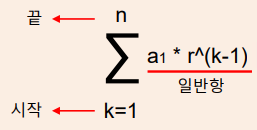
1. 시그마

• 

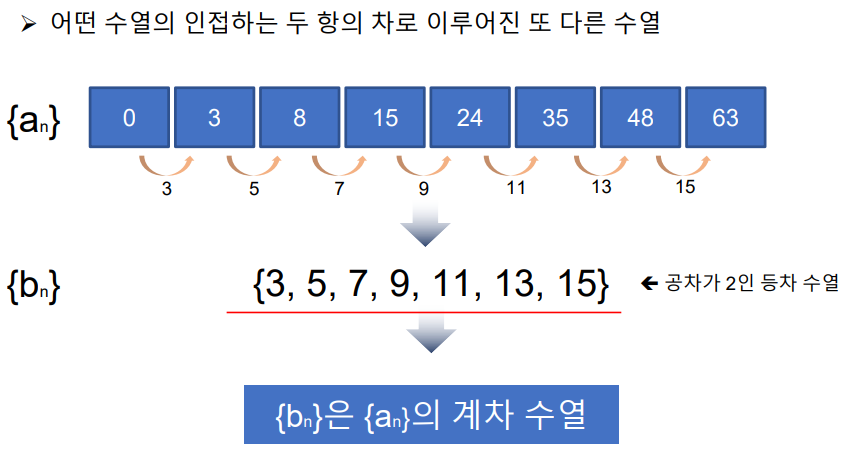
2. 계차수열

• 

실습1.

• 

inputA1 = int(input('A1 의 값: '))
inputAN = int(input('n번째 항 : '))
inputBN1 = int(input('b1 의 값'))
inputBD = int(input('bn의 공차 입력: '))

valueAN = 0
valueBN = 0
n = 1

while n <= inputAN:
    if n == 1:
        valueAN = inputA1
        valueBN = inputBN1
        print(f'A{n}항 : {valueAN}',end=', ')
        print(f'B{n}항 : {valueBN}')
        n+= 1
        continue
    valueAN += valueBN
    valueBN += inputBD
    print(f'A{n}항 : {valueAN}',end=', ')
    print(f'B{n}항 : {valueBN}')
    n+=1

A1 의 값: 3
n번째 항 : 5
b1 의 값4
bn의 공차 입력: 2
A1항 : 3, B1항 : 4
A2항 : 7, B2항 : 6
A3항 : 13, B3항 : 8
A4항 : 21, B4항 : 10
A5항 : 31, B5항 : 12

3. 피보나치 수열

실습1. 피보나치 수열의 n항 값 구하는 코드

inputN = int(input('n번째 항 의 값: '))
valueN = 0
valuePreN1 = 0
valuePreN2 = 0

sumN = 0
n =1

while n <= inputN:
    if n == 1 or n == 2:
        valueN = 1
        valuePreN1 = valueN
        valuePreN2 = valueN
        n+=1

    else:
        valueN = valuePreN2 +valuePreN1
        valuePreN2 = valuePreN1
        valuePreN1 = valueN
        n += 1

print(f'{inputN}번째 항 : {valueN}')

n번째 항 의 값: 9
9번째 항 : 34

4. 팩토리얼

• 1부터 양의 정수 n까지의 정수를 모두 곱한 값
• n!

실습1. 입력한 숫자의 팩토리얼 값 구하기

inputNum = int(input('숫자 입력: '))
result = 1
for i in range(1,inputNum+1):
    result *= i
print(f'{inputNum}의 팩토리얼 : {result}')

숫자 입력: 4
4의 팩토리얼 : 24

실습2. 재귀함수를 이용한 팩토리얼 값

• 재귀함수 : 자기 자신을 호출하는 함수

inputN = int(input('n 입력:'))
def factorialFun(n):
    if n == 1:
        return n
    return n * factorialFun(n-1)

print(f'{inputN}의 팩토리얼 값 : {factorialFun(inputN)}')

n 입력:4
4의 팩토리얼 값 : 24

5. 군수열

• 

실습1. 입력한 n번째 항 구하기

inputN = int(input('n항 입력: '))
flag = True
n = 1
nCnt = 1
searchN = 0

while flag:
    for i in range(1,n+1):
        print(f'{i}',end='')
        nCnt+=1

        if nCnt > inputN:
            searchN = i
            flag = False
            break
    print()
    n+=1
print(f'{inputN}번째 항 : {searchN}')

n항 입력: 20
1
12
123
1234
12345
12345
20번째 항 : 5

6. 순열(nPr)

• n개에서 r개를 택하여 나열하는 경우의 수 (단, 순서 중요)
• ex) 1,2,3 뽑을 수 있는 경우의 수는 (123)(132)(213)(231)(312)(321) 총 6가지
• 공식
  

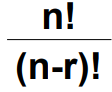
실습1. 입력받은 n개에서 r개 뽑는 경우의 수(0<r<=n)

inputN = int(input('n 입력: '))
inputR = int(input('r 입력: '))

result = 1

for i in range(inputN, inputN-inputR, -1):
    print(f'{i}')
    result *= i

print(f'{inputN}개 에서 {inputR}개 뽑는 경우의 수 : {result} ')

n 입력: 5
r 입력: 3
5
4
3
5개 에서 3개 뽑는 경우의 수 : 60 

7. 원순열

• 시작과 끝의 구분이 없는 순열
• 공식
  

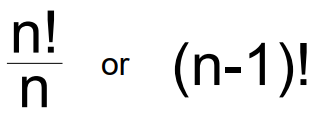
실습1. 원형 테이블에 친구가 앉을 수 있는 경우의 수

inputN = int(input('친구 수 입력 : '))
result = 1

for i in range(1,inputN):	#(n-1)!이므로 range(1,n) 은 1~n-1이다
    result*=i
print(f'{inputN}명의 친구가 원형테이블에 앉을 경우의 수 : {result}')

친구 수 입력 : 4
4명의 친구가 원형테이블에 앉을 경우의 수 : 6

8. 조합(nCr)

• 순서 상관 없이 n개 에서 r개 선택
• 공식
  

실습1. 입력받은 n개에서 r개 뽑는 경우의 수(순서 상관 없음)

• 공식을 이용해서 하기

numN = int(input('n 입력: '))
numR = int(input('r 입력: '))

resultP = 1
resultR = 1
resultC = 1

for i in range(numN, numN-numR, -1):
    resultP *= i
for n in range(1,numR+1):
    resultR *= n

resultC = int(resultP / resultR)
print(f'{numN}에서 {numR}개 순서상관 없이 뽑는 경우의 수 : {resultC} ')

n 입력: 7
r 입력: 5
7에서 5개 순서상관 없이 뽑는 경우의 수 : 21 

9. 확률

• 모든 사건에서 특정 사건이 일어날 수 있는 수를 나타내는 것
  모든사건 = 표본공간(sample)
  특정사건 = 사건(event)

실습1. 꽝,꽝,꽝,꽝,선물,선물,선물 중 꽝 2개 선물 1개 뽑는 확률은?

def Combination():
    numN = int(input('n 입력: '))
    numR = int(input('r 입력: '))

    resultP = 1
    resultR = 1
    resultC = 1

    for n in range(numN, numN-numR,-1):
        resultP *= n
    for n in range(1,numR+1):
        resultR *= n
    resultC = resultP/resultR

    return resultC

sample = int(Combination())
print(f'총 뽑을 수 있는 경우의 수 : {sample}')

event1 = int(Combination())
print(f'꽝2장 뽑는 경우의 수 : {event1}')

event2 = int(Combination())
print(f'선물 1장 경우의 수 : {event2}')

percent = round(event1 * event2 / sample * 100,2)

print(f'{percent}%')

n 입력: 7
r 입력: 3
총 뽑을 수 있는 경우의 수 : 35
n 입력: 4
r 입력: 2
꽝2장 뽑는 경우의 수 : 6
n 입력: 3
r 입력: 1
선물 1장 경우의 수 : 3
51.43%