LCS

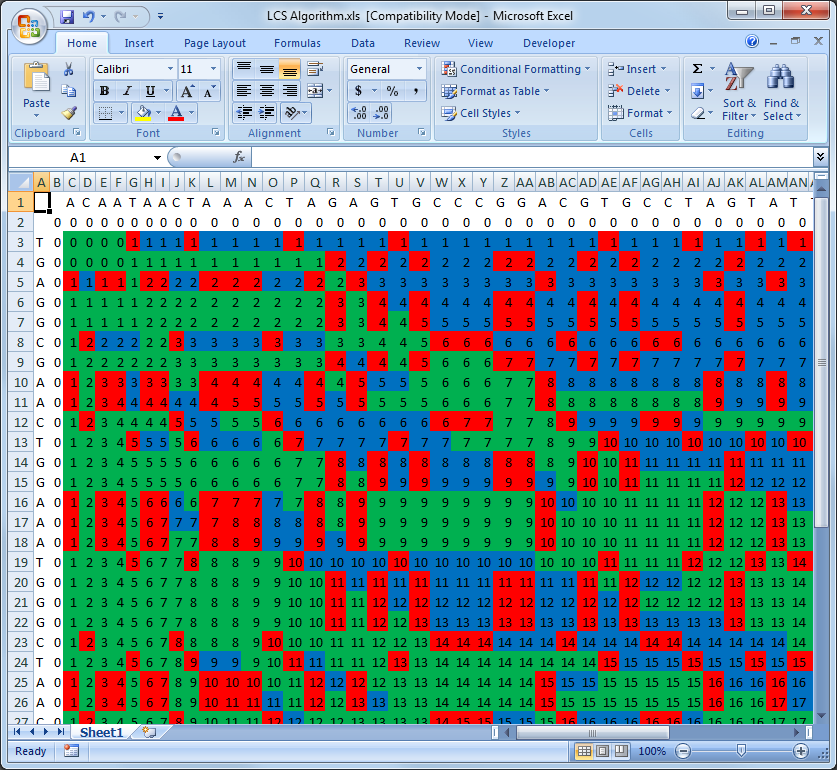
1.LCS란?

LCS는 주로 최장 공통 부분수열(Longest Common Subsequence)을 말하지만 최장 공통 문자열(Longest Common Substring)을 말하기도 한다.

Subsequence와 Substring의 차이는 ABCD,ABED라는 두 문자열이 있을때 Subsequence의 경우 연속하지 않아도 되기에 정답 문자열이 ABD가 되지만 Substring의 경우 무조건 연속적으로 공통적인 문자열만 구하기에 AB가 된다.

1-1. Substring

Substring은 연속적인 문자열만 구하면 되기때문에 쉬운 편이다. 알고리즘의 작동은 이렇다.

• A문자열의 길이를 i, B문자열의 길이를 j라고 한다.

• dp[0][0]부터 dp[i + 1][j + 1]까지 모두 0으로 초기화한다.
  (i+1,j+1로 초기화 하는 이유는 0부터 시작할시 배열을 벗어나기 때문이고, 0으로 초기화 하는 이유는 두 문자열이 같을때만 값을 업데이트 해주면 되기 때문이다.)

• 문자열A, 문자열B의 한글자씩 비교한다.

• 두 문자가 같다면 dp[i - 1][j - 1] 값을 찾아 +1 한다.

위 과정을 문자열 끝까지 반복한다.

dp[i - 1][j - 1]가 의미 하는것은 자신 앞글자까지의 공통 부분을 가져 오는것이다.

for i in range(len(A)):
    for j in range(len(B)):
        if A[i] == B[i]:
            dp[i][j] == dp[i-1][i-j] + 1
            result = max(dp[i][j],result)
            
print(result)
            #갱신될때마다 최대값 비교해서 저장한다.

시간복잡도는 O(n*m) 이다.

1-2. Subsequence

그렇다면 이번에는 다른 LCS인 최장 공통 부분수열(Longest Common Subsequence)를 만들어 보겠다.

• A문자열의 길이를 i, B문자열의 길이를 j라고 한다.

• dp[0][0]부터 dp[i + 1][j + 1]까지 모두 0으로 초기화한다.

• 문자열A, 문자열B의 한글자씩 비교한다.

• 두 문자가 같다면 dp[i - 1][j - 1] 값을 찾아 +1 한다.

• 두 문자가 다르다면 dp[i - 1][j] 와 dp[i][j - 1] 중 큰 값을 가져와 dp[i][j]에 저장해준다.

Substring과 차이점은 두 문자열이 같지 않을 때에도 값을 업데이트 해주는 것이다.

dp[i - 1][j] 와 dp[i][j - 1] 의미는 연속적인 부분공통수열이 아니므로 현재의 문자를 비교하는 과정 이전의 최대 공통 부분수열은 계속해서 유지된다. '현재의 문자를 비교하는 과정' 이전의 과정이 바로 dp[i - 1][j]와 dp[i][j - 1]가 된다.

for i in range(len(A)):
    for j in range(len(B)):
        if A[i] == B[i]:
            dp[i][j] == dp[i-1][i-j] + 1
            result = max(dp[i][j],result)

        else:
            dp[i][j] = max(dp[i-1][j],dp[i][j-1])

print(dp[N][M])

1-3. LCS 문자열 구하기

지금까지는 수열이 몇개로 구성되었는지 구하는거였다면 이제는 직접적으로 수열을 구해야한다.

우선 Substring의 경우에는 쉽게 temp 라는 빈 문자열과 resultLine이라는 결과 값을 저장할 빈 문자열을 만든다. 비교하는 문자열 값이 같을때마다 temp 문자열에 값을 저장하다가 현재의 부분문자열의 최대 길이가 갱신되면 temp의 값을 result에 저장하는 방식을 생각 할 수 있다.

하지만 Subsequence와 같은 경우는 다르다. 수행방법은 다음과 같다.

• dp배열의 가장 마지막(n,m)에서 시작한다. 결과를 저장할 result 배열을 준비한다.

• dp[i-1][j] 와 dp[i][j-1] 값 중 현재 값과 같은 값을 찾는다.

  • 있다면 그 전의 값을 가져왔으므로 현재 문자는 공통부분에 속하지 않는다. 값을 가져온 곳으로 이동한다.
  • 없다면 내가 부분배열의 공통 부분이다. result 배열에 자신의 값을 넣는다. dp[i-1][j-1]로 이동한다.

• 이전 항목을 반복하다가 0에 도착하면 종료한다.

  i, j = n, m
  result = ""
  while i == 0 or j == 0:
  
     if dp[i][j] == dp[i-1][j]:
         i -= 1
     elif dp[i][j] == dp[i][j-1]:
         j -= 1
     else:
         result += A[i] #A문자열이나 B문자열 아무것이나 가져와서 넣으면 된다.
         i -= 1
         j -= 1
  
  print(result[::-1])