🎲[알고리즘] 재귀함수

이강욱·2022년 10월 2일

정글 정글 / PS

🎲 알고리즘

목록 보기

1/5

아픈 손가락(?)

1주차가 끝나고 운영진 분들이 참석하신 티타임에서 한 분이 질문을 하셨다.

"재귀함수가 많이 헷갈리는데 현업에서도 많이 사용하나요?"

대표님 답변.

'더하기 많이 써요?' 같은 질문이라고 생각하면 돼요. ~~(아.)~~

언젠간 정리를 해보고 싶었다.
쉬운 문제들을 풀면서 보였던 패턴이나, 백트래킹, 분할정복 같은 개념도 간단히 정리해보고자 한다.
파이썬 책(Do it! 시리즈)을 참고했다.

재귀 (Recursion)

전체적인 이해

나는 재귀를 다음과 같은 비유적 상황으로 이해했다.

전체 문제상황에서 처리해야할 범위를 분할해서 각각을 떠넘기거나, 또는 최소단위 하나만 챙기고 나머지를 다시 떠넘긴다.

떠넘기다 남은 문제상황이 최소단위 하나가 되면
그때 알맞은 반환값을 반환하거나 저장(외부에 선언된 배열, 변수 등에)한다.

위의 그림은 2번에서의 반환 상황의 두가지 종류를 보여준다.

왼쪽 그림은 상향식으로 결과를 계산한다. 최소단위(Terminating case, Base case)에서 반환한 값을, 바로 위 재귀호출이 자신이 가지고 있던 하나와 함께 계산해서 다시 반환한다.
그 과정이 반복되면 최초 재귀호출의 반환값이 전체 문제상황의 해결값이 되는 것이다.
오른쪽 그림은 하향식으로 결과를 계산한다. 전체 문제상황의 해결값을 저장하는 paramter 자리를 하나 만들고, 아래 재귀에게 자신이 가지고 있던 하나를 추가(또는 필요한 연산)한 값을 전달한다. 이 과정이 반복되면서 재귀의 밑바닥(최소단위까지 연산 완료 된 후)에 도착했을 때는, 바로 위 재귀에서 보내준 값이 곧 전체 문제상황의 해결값이 된다. 바로 그 값이 재귀를 탈출하면서 연속적으로 반환되게 되고, 최초 재귀 호출의 반환값이 최소단위에서 반환한 그 값이 된다.

코드로 보면 다음과 같다.

# 왼쪽 (상향식)
def sumVector(A, n):
   if n == 1:
      return A[0]
   else:
      return A[n-1] + sumVector(A,n-1)

# 오른쪽 (하향식)
def sumVector(B, n, sum):
   if n == 0:
      return sum
   else:
      return sumVector(B,n-1,sum+B[n-1])

오른쪽의 경우를 꼬리 재귀(tail recursion)라고도 한다. 만약 컴파일러가 꼬리 재귀 최적화를 지원한다면, 꼬리 재귀는 연속적인 재귀 호출로 일어나는 stack의 오버헤드를 줄일 수 있다.

두번 이상 호출 될 때

재귀 호출이 함수 내에 두번 일어날 수도 있다. 책에서는 다음의 재귀함수를 소개한다.

def recur(n):
	if n > 0:
    	recur(n - 1)
        print(n)
        recur(n - 2)

오묘하게도 이러한 재귀 호출을 비재귀적으로 바꾸는 과정에서 함수를 이해할 수 있다.

1. 뒤에 나오는 재귀

먼저 뒤에 나오는 재귀 recur(n - 2)를 없애보자. 해당 호출은 이런 의미이다.

인수로 n-2 의 값을 전달하고 recur( )함수를 호출해라.

재귀를 없앤다는 것은 recur()함수의 호출을 없앤다는 것. 따라서 아래와 같은 방안이 있다.

n의 값을 n -2로 업데이트 한 후, 함수의 시작지점으로 돌아가면 된다.

이를 적용한 코드이다.

def recur(n):
	while n > 0:
    	recur(n - 1)
        print(n)
        n = n - 2 	# 업데이트 한후, while 반복문 다음 루프.(시작지점으로 돌아가기)

2. 앞에 나오는 재귀

앞에 등장하는 재귀는 위와 같은 방법으로는 제거할 수 없다.
왜냐하면 n값을 업데이트(n = n - 1)하고 시작지점으로 돌아가면, print(n)이 올바르게 실행 될 수 없기 때문이다. 다시 말해, 현재 루프의 n의 값을 임시로 저장해야 한다. 그래서 recur(n - 1)의 처리를 끝낸 후에 저장했던 n의 값을 꺼내 print(n)해줘야 한다.

결국 스택을 사용하여 n의 값을 저장해야 한다.

이를 적용한 코드이다.

from collections import deque
def recur(n):
	stk = deque()	# 스택으로 사용할 덱.
	while True:
    	while n > 0:
        	stk.append(n)	# 스택에 n부터 1씩 줄여나가면서 저장. 현재 루프의 'n'을 저장한다는 의미.
            n = n - 1
            
    	if stk:
        	n = stk.pop()
            print(n)
        	n = n - 2 	# 업데이트 한후, while 반복문 다음 루프.(시작지점으로 돌아가기)
            continue	# 무한 while로 복귀
        break

스택 저장 과정이 끝나고, stk.pop()을 통해 맨 위의 값(가장 작은 값이 되겠다. 여기서는 1)을 꺼낸뒤, 프린트 하고, n = n - 2를 해서 시작점으로 돌아오면 아까 그 스택에 다시 값들을 쌓는다. 즉, 호출 순서가 지켜지는 것이다.

분할 정복 (Divide & Conquer)

나폴레옹의 전술에서 유래했다. 개괄하면 다음과 같다.

Divide an instance of a problem into one or more smaller instances.

Conquer(solve) each of the smaller instances. Unless a smaller instance is sufficiently small, use recursion to do this.

If necessary, combine the solutions to the smaller instances to obtain the solution to the original instance.

큰 사이즈의 문제 instance를 최대한 작게 나누어 각각 해결한다. 그리고 필요에 따라 이 결과들을 combine한다. 최대한 작게 나누어 해결 하는 과정에서 재귀적인 방법이 쓰인다.
그렇게 크지 않은 사이즈의 문제에서는 유용하지 않을 수 있다.
대표적인 활용으로는 이진 탐색, 병합 정렬, 퀵 정렬, 행렬 곱셈, 최근접 점의 쌍(closest Pair Problem) 이 있다.

백트래킹 (Backtracking)

아래는 N-queen 문제의 상태 공간 트리.

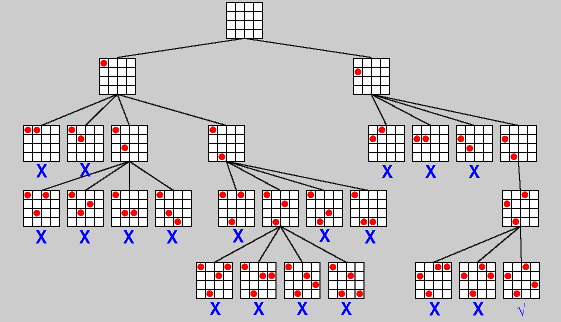
백트래킹(back-tracking)이란 상태 공간 트리(state space tree)를 탐색하는 기법 중 하나.
다음과 같은 탐색 기법들이 있다.

0. Brute Force Method
말 그대로 짐승같이 무식하게 모든 경우의 수를 다 검사해보는 방법이다. 조금 정제된 말로는
Solution space를 모두 탐색하여 해를 얻는 방법이다. instance의 사이즈가 작을 경우 오버헤드가 적어 효율적이다.

1. 완전탐색(Exhaustive Search)
모든 경우의 수를 다 검사하여 해를 찾는 방법이다. Brute Force Method의 일종으로, 거의 같은 의미로 쓰인다. 보통 완전탐색은 순열이나 조합(permutational or combinational-related)으로 경우의 수를 생성해서 전부 탐색하는 경우를 의미한다.

It is a brute-force approach to deal with combinatorial problems (permutations, combinations). In this approach, we generate each element in the problem and then select the ones that satisfy all the constraints, and finally find a desired element.
...
출처: https://towardsdev.com/brute-force-and-exhaustive-search-f431484e5293

2. 백트래킹(Backtracking)
완전탐색의 방법과 유사하지만, 가지치기(pruning)를 하여 더 효율적이다.
위의 그림과 같이 분기에서 '막히면'(= not promising 하면 = 이 분기의 하위 탐색이 의미가 없으면) 그 하위 분기를 탐색하지 않는다.
promising 함수를 따로 구현하는 경우가 많다. DFS(Depth-First-Search)로 구현.

3. 분기 한정 기법(Branch & Bound)
백트래킹에서 '가지치기'의 기준 즉, promising함수의 판정이 상태 공간 트리 각 노드의 한정값에 의존한다. 백트래킹 기법보다 빠르게 해를 찾는다. 가장 우수한 한정값을 가진 노드를 먼저 탐색하는 최우선 탐색(Best First Search)으로 해를 찾는다. Best Fisrt Search와 Breadth First Search의 차이점은 (여기를 참고).

동적프로그래밍 (DP : Dynamic Programming)

동적 계획법

프로그램 실행 중에 작은 답들을 찾아서 그것을 활용한다는 점에서 동적.
static vs dynamic 에서의 dynamic과는 관련이 없다.

최적 부분 구조 (Optimal Substructure)

큰 문제를 작은 문제로 나눌 수 있고, 작은 문제들의 답을 모아서 큰 문제를 해결할 수 있다.

메모이제이션(memoization)

'이미 계산된 결과를 메모리에 저장' ➡️ 메모이제이션
함수의 반환값 DP 테이블에(주로 배열) 캐싱.
하지만 메모이제이션과 DP는 별개의 개념.
탑다운 방식에서 메모이제이션을 '사용'하는 것 뿐.

탑다운(재귀) vs 바텀업(반복문)

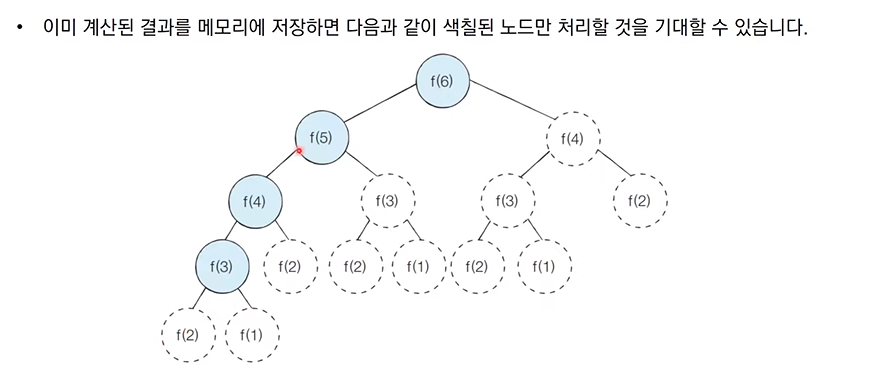
탑다운의 재귀호출에서 위의 그림과 같이 매우 많은 분기가 생길 수 있지만, 메모해둔 값을 얻어와서 하위 분기를 생성하지 않는다.
바텀업 방식에서는 점화식에 충실하게 배열을 왼쪽부터 채워나간다. 메모이제이션과는 살짝 다르다.
전형적 형태는 바텀업.
연습하기에는 탑다운이 좋다.(코치님)

다이나믹 프로그래밍 vs 분할 정복
'부분 문제의 중복' 여부의 차이

피보나치 수열
역시 피보나치 수열이 가장 좋은 예시.

a_n = a_n-1 + a_n-2, a_1 = 1, a_2 = 1

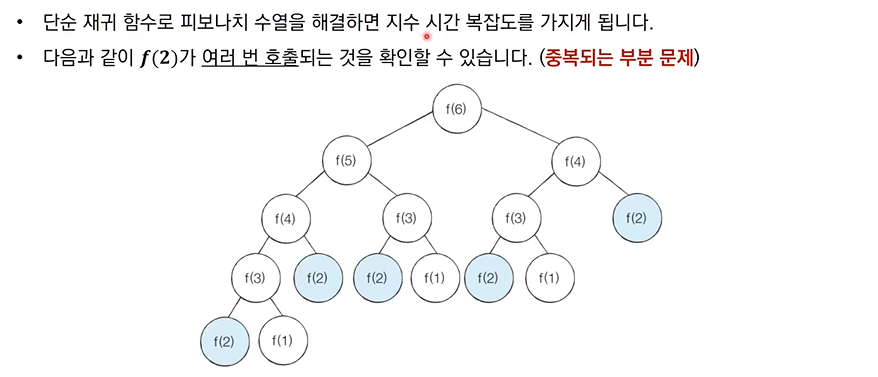
⬆️ 위의 그림은 메모이제이션 없이 재귀호출을 계속하는 경우.
⬇️ 아래는 탑다운 방식의 DP를 통해(/w 메모이제이션) 하위 분기를 생성하지 않게 되는 경우.

🐍 파이썬 코드 (피보나치 수열 99번째 항 구하기).

# dp 테이블
d = [0] * 100

###############################################################
# 탑다운 다이나믹 프로그래밍
# 재귀함수와 메모이제이션으로 구현
def fibo(x):
	if x==1 or x==2 :
    return 1
    
    # 이미 값이 구해져 있는 경우 그 값을 반환
    if d[x] != 0:
    	return d[x]
    # 아니라면 점화식 따라 재귀호출
    d[x] = fibo(x-1) + fibo(x-2)
    return d[x]
    
print(fibo(99))

###############################################################
# 바텀업 다이나믹 프로그래밍
# 반복문을 이용
# dp 테이블 초기화
d = [0] * 100

# 첫 값(?)
d[1] = 1
d[2] = 1
n = 99

for i in range(3, n+1):
	d[i] = d[i-1] + d[i-2]

print(d[n])

참고 페이지

이강욱

I think I think too much.

다음 포스트