문제

https://www.acmicpc.net/problem/27498

풀이

문제에서 주어진 조건들을 하나씩 살펴보자

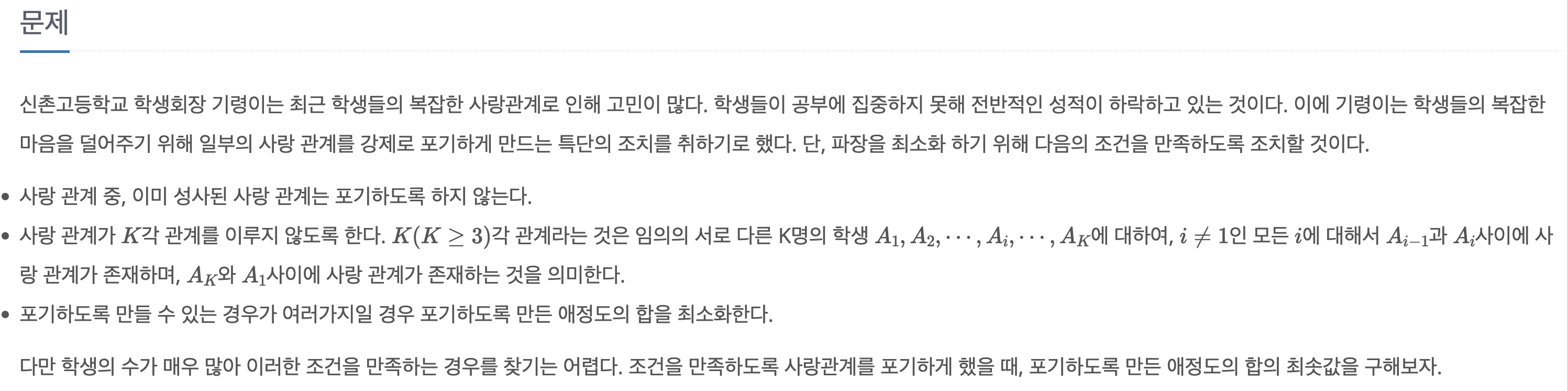
• 사랑 관계 중, 이미 성사된 사랑 관계는 포기하도록 하지 않는다.
  : 이미 성사된 관계는 포기할 수 없다 -> 반드시 이어져야하는 관계가 따로 주어진다.

• 사랑 관계가 $K$각 관계를 이루지 않도록 한다. $K$$(K \geq 3)$각 관계라는 것은 임의의 서로 다른 K명의 학생
  $A_1, A_2, \cdots, A_i, \cdots, A_K$에 대하여, $i \neq 1$인 모든 $i$에 대해서 $A_{i-1}$과 $A_{i}$사이에 사랑 관계가 존재하며,
  $A_K$와 $A_1$사이에 사랑 관계가 존재하는 것을 의미한다.
  : 구하고자 하는 사랑관계가 스패닝 트리가 됨을 알 수 있다.

• 포기하도록 만들 수 있는 경우가 여러가지일 경우 포기하도록 만든 애정도의 합을 최소화한다.
  : 말 그대로 없애야 하는 총 간선의 합을 최소화 해야한다.

다음 조건들을 정리하여 생각해보자.
가중치의 합이 최대가 되도록 하는 신장트리를 만들고 전체 가중치의 합에서 그 신장트리의 합의 차를 구해주면 된다.
단, 이때 반드시 union 되어야하는 간선은 따로 주어지므로 해당 간선들을 미리 union 시키고 나머지 간선들에 대하여
가중치 기준으로 내림차순 정렬 후 크루스칼 알고리즘을 진행하면 된다.

CODE

import sys

input = sys.stdin.readline


def solve():
    n, m = map(int, input().split())
    edges = []
    total = 0
    success_sum = 0
    par = [-1 for _ in range(n+1)]

    def find(cur):
        if par[cur] < 0:
            return cur
        par[cur] = find(par[cur])
        return par[cur]

    def union(u, v):
        u, v = find(u), find(v)
        if u == v:
            return False
        if par[u] < par[v]:
            u, v = v, u
        par[v] += par[u]
        par[u] = v
        return True

    for i in range(m):
        u, v, val, is_union = map(int, input().split())
        total += val
        # 조건 1 : 이미 성사된 사랑 관계
        if is_union:
            success_sum += val
            union(u, v)
        else:
            edges.append([u, v, val])
    # 가중치 기준 내림차순 정렬
    edges = sorted(edges, key=lambda x: -x[2])
    
    for u, v, val in edges:
        if union(u, v):
            success_sum += val

    print(total - success_sum)


solve()