이전 글에서 공부한 Symmetric Ciphers 에서 송신자와 수신자는 같은 key 를 가집니다. 그렇다는 것은 이 key를 사전에 공유하여야 한다는 것을 의미하기도 합니다.

Key Sharing

하지만 인터넷에서는 서로가 누구인지를 모를 뿐더러 결과 완전히 안전한 채널이 존재하지도 않습니다. 그렇다면 어떻게 key를 안전한 방식으로 공유할 수 있는 것일까요?

발상을 좀 바꿔봐야 합니다.

아래의 예시를 보시죠.

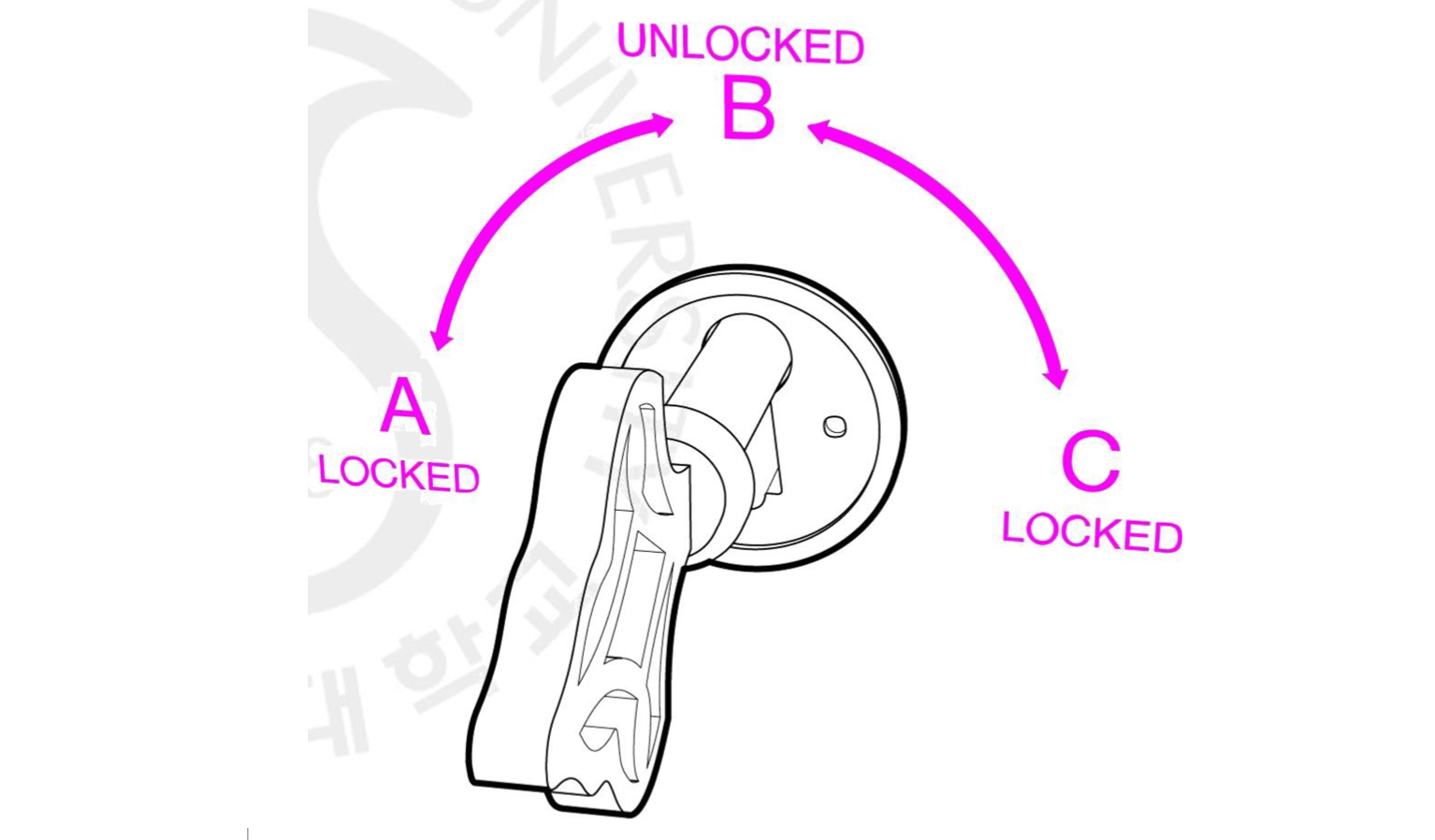
위와 같은 이 A와 C는 잠긴 상태, B는 열린 상태로 하는 lock이 있습니다. 그리고 이 lock에 쓸 수 있는 key는 두 가지 타입이 존재합니다. 첫 번째 key는 A - B - C 로 시계 방향으로만 동작합니다. 두 번째 key는 C - B - A 로 반시계 방향으로만 동작합니다. 이 때 주인인 Alice는 첫 번째 자신이 첫 번째 key를 가지고 두 번째 key는 복사해서 여러 사람들에게 뿌립니다.

그렇기 때문에 Alice가 가진 첫 번째 key가 Private Key, 나눠준 key가 Public Key 가 되는 것입니다. 이게 어떻게 가능할까요? 다음과 같은 상황을 생각해봅시다. 두 번째 key의 복사본을 가진 Bob은 Alice에게 비밀리에 서류를 전달하기 위해 박스에 담아 시계 반대방향으로 A로 박스를 잠굽니다. 그렇게 되면 이 박스를 B로 돌려 풀 수 있는 것은 첫 번째 key를 가진 Alice 만이 유일무이하게 됩니다. 박스 안의 서류가 안전하게 되는 것이죠.

이와 같은 상황 또한 가능합니다. Bob이 Alice에게 돈을 빌려주고 Alice가 차용증을 써서 박스에 담아 자신의 key를 이용해 C 방향으로 잠갔습니다. 그런데 Alice가 자신은 빌린 적이 없다며 발뺌하는 것입니다. 화가 난 Bob은 박스를 가지고 법정에 가서 박스를 엽니다. 박스를 C에 놓을 수 있는 것은 오직 Alice 밖에 없기 때문에 박스 안 서류는 Bob이 썼을 리가 없는 것이죠. Alice는 부정을 못하게 되는 것입니다. 기본적인 Asymmetric 의 이론입니다. 실제로 이것이 우리가 사용하고 있는 Digital Signature 의 원리이기도 하죠.

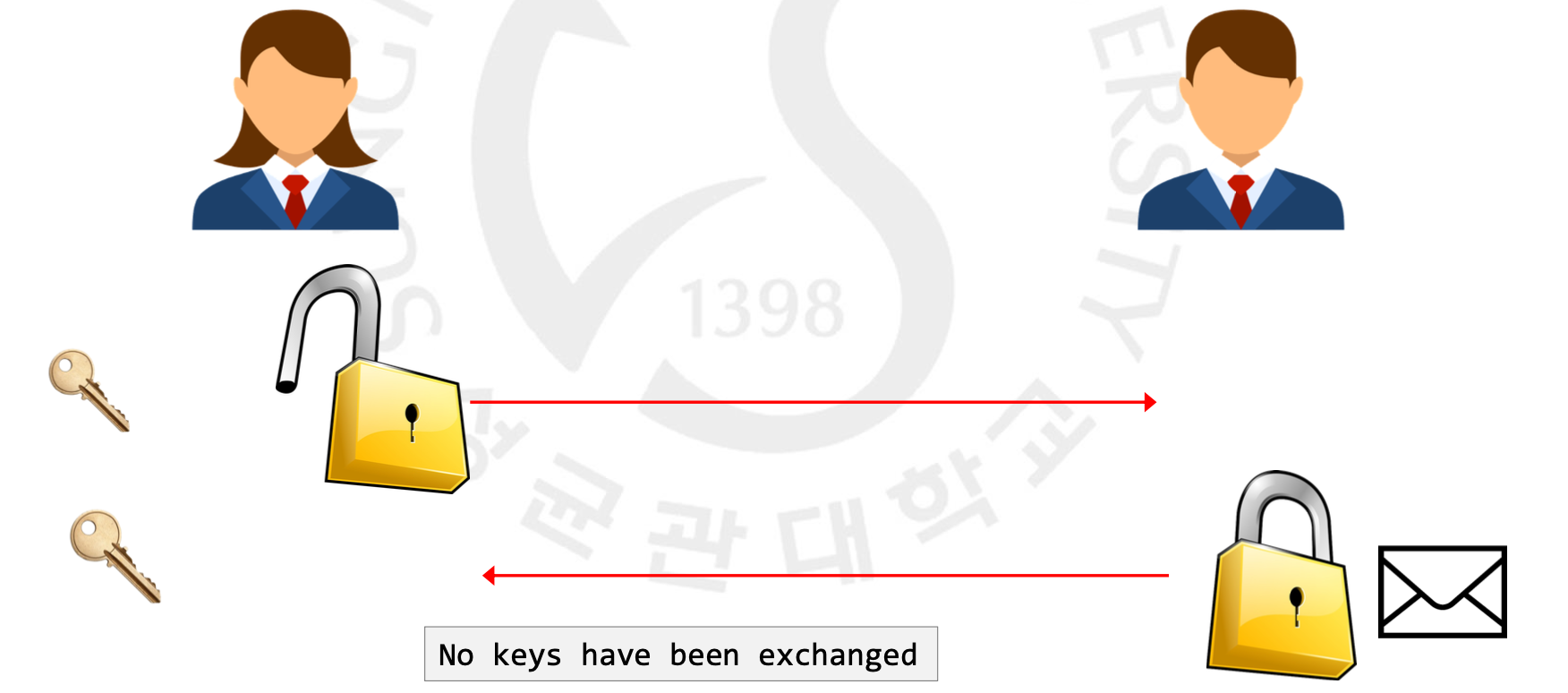
간단히 표현하면 위 그림과 같습니다. Alice는 lock을 잠그지 않고 Bob에게 줍니다. 그러면 Bob은 메시지를 넣고 lock을 잠그는 것이죠. 다시 Alice에게 보내면 key를 가지고 있는 Alice만이 이 lock을 풀어 내용을 확인할 수 있게 되는 겁니다.

이러한 Non-Secret Encryption 방식은 key를 공유하지 않기 때문에 비밀이 밖으로 나가지 않는다는 강력한 장점을 가집니다. 이것이 동작할 수 있는 이유는 즉 잠그는 것은 쉬운 데 반해 푸는 것은 매우 어렵기 때문입니다. 누구나 열쇠가 없는 사람도 잠그는 lock 과정은 할 수 있으나 그것을 푸는 unlock 과정은 열쇠가 있는 사람만이 풀 수 있는 것입니다.

한 쪽(lock)은 쉽고, 다른 쪽(unlock)은 어렵게 하는 ONE-WAY 방식입니다. 이와 같이 우리는 하나는 어렵고 하나는 쉬운 상반되는 두 개의 operation을 찾아 쉬운 건 공개해 버리고 어려운 것을 자신만이 갖고자 하는 겁니다. 이것이 바로 가장 중요한 원리입니다.

한 가지 비유로는 색을 섞는 것을 들 수 있습니다. 우리가 임의로 초록과 빨강의 섞어 노란색을 만들었다 해봅시다. 이 노란색을 다른 많은 사람들에게 알려준다 한들, 이 것이 초록과 빨강의 조합이라는 것을 알기는 쉽지 않습니다. 노란색을 만들기 위한 너무 많은 경우의 수가 존재하기 때문이죠. 섞는 것은 쉽고 분리하는 것은 어려운 ONE-WAY 방식입니다.

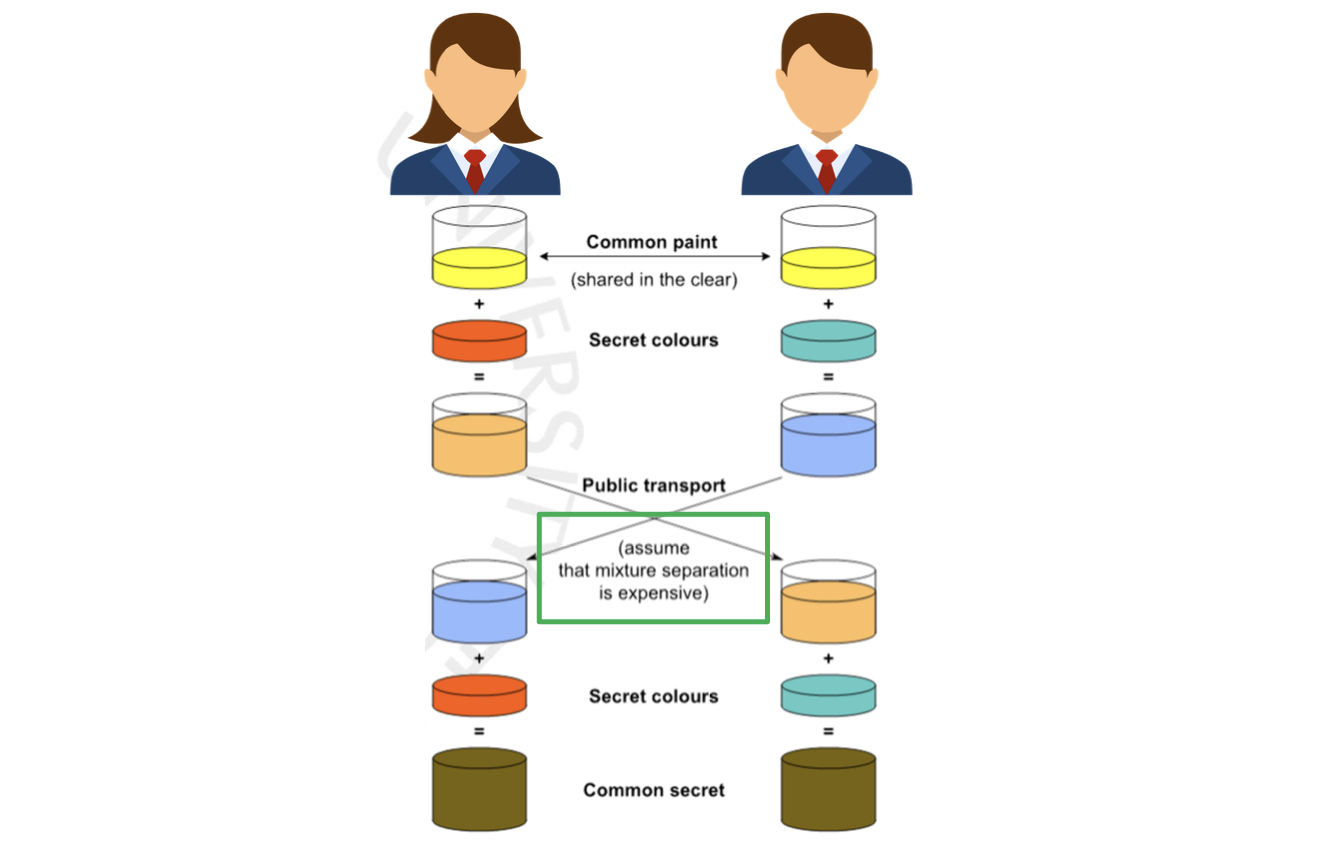
원리 이해를 이해 예시를 하나 더 살펴봅시다. 먼저 Alice와 Bob은 시작하는 색을 노랑으로 합의를 본 것으로 시작합니다. 그 다음에 자신만의 private 한 색을 섞어 새로운 색을 만들고 이를 public 으로 서로에게 전송합니다. 공격자가 이 색을 안다한들 조합을 찾기는 매우 힘듭니다. 받은 서로의 색에 자신의 색을 더하면 같은 두 가지 색이 섞인 최종의 색은 같게 됩니다. 누구도 알면 안되는 자신만의 색은 Prviate Key, 시작하는 색과 섞인 색들은 누가 봐도 상관이 없는 Public Key 가 되는 겁니다. 나만 알고 있어야 하는 공인인증서 비밀번호는 private key, 관리하는 금융결제원에서 갖고 있는 것은 public key 인 것이죠. 이제 감이 오시죠??

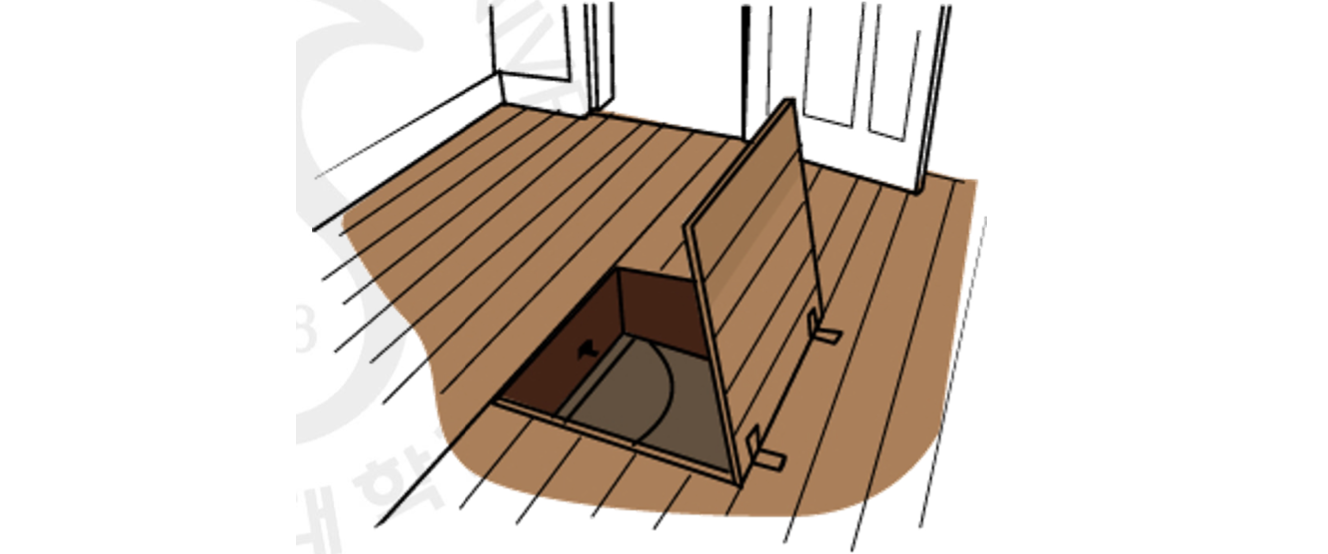
결국 우리가 하고 싶은 것은 바로 Trapdoor Function 을 찾는 것입니다. 한 쪽으로는 계산이 쉽고 다른 쪽으로는 계산이 어려운 함수를 뜻합니다. ONE-WAY 와 다른 점은 Trapdoor Function 은 어려운 계산도 trapdoor 라는 단서의 도움이 있으면 쉽게 풀린다는 점입니다. 위와 같은 아무것도 없는 깊은 지하 구멍이 있을 때 뛰어 내려가는 건 쉽고 밑에서 올라오는 것은 불가능에 가깝습니다. 하지만 사다리라는 trapdoor 가 있으면 단 번에 올라오는 것이 쉬어지죠.

Number Theory

이러한 Trapdoor Function 을 찾기 위해 우리는 수학을 조금 해야 합니다. 그것이 바로 Number Theory(정수론) 이죠. 우리가 주목해야 해야 할 것은 Modular(나머지) 연산입니다.

46을 12로 나눈 것은 10 이고 이는 10을 12로 나눈 것과 같습니다. 이를 수식으로 표현하면 다음과 같습니다.

$46\mod\ 12 \equiv 10 \mod \ 12$

이를 우리는 modulus 12 상에서 46과 10이 Congruent 하다(동치 이다)라고 표현하며 아래와 같이 줄여서 씁니다.

$46 \equiv 10\ (mod \ 12)$

그리고 $modular\ n$ 상에서 모든 수의 집합 은 $n$으로 나누었을 때 나올 수 있는 나머지인 $Z = \{0, 1, 2, ...,(n-1)\}$ 이 됩니다. 이를 알았다면 Modular 연산의 여러 특징들을 알아보도록 합시다.

만약 $a \equiv b\ (mod\ N)$ 일 때, 다음을 만족합니다.

• 아무 정수 $k$에 대해
  $a + k \equiv b + k\ (mod\ N)$ (translation)
• 아무 정수 $k$에 대해
  $ka \equiv kb \ (mod\ N)$ (scaling)
• 아무 양의 정수 $k$에 대해
  $a^k \equiv b^k \ (mod\ N)$ (exponentiation)
• 하지만 다음은 불가능 합니다!
  $k^a \equiv k^b \ (mod\ N)$

또 중요한 특징으로는 다음이 있습니다.

$k$ 가 $N$ 과 서로소일 때
$ka \equiv kb \ (mod \ N)$ 이라면 $a \equiv b \ (mod \ N)$

또 정말 특이한 다음과 같은 특징을 기억해야 합니다. 우리 $a$의 Multiplicative Inverse(곱셈의 역원) $a^{-1}$은 $\frac{1}{a}$ 이라는 것을 압니다. 그러나 모듈러 상에서는 정수만을 취급합니다. 그래서 $a^{-1}$ 또한 정수이죠. 이는 다음과 같은 특징을 가집니다.

$a$ 가 $N$ 가 서로소 일 때 $aa^{-1} \equiv 1 \ (mod \ N)$ 을 만족하는 $a^{-1}$ 이 존재한다.

아래 예시를 보겠습니다.

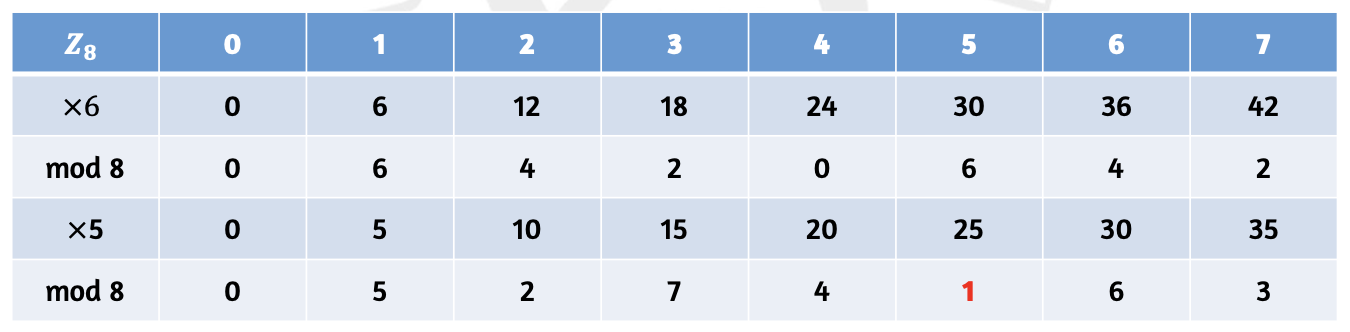
6의 경우에는 나누는 8과 서로소가 아니기 때문에 0부터 7까지 곱해봐도 모듈러 값이 1인 경우가 나오지 않습니다. 5는 8과 서로소이기 때문에 5에서 모듈러 값이 1이 나올 수 있는 것입니다.

Fermat's Theorem(페르마의 정리)

다음으로 알아야 할 것이 Fermat's Theorem(페르마의 정리) 입니다. 내용은 다음과 같습니다.

$p$가 소수이고 $a$가 $p$와 서로소인 양의 정수일 때
$a^{p-1} \equiv 1 \ mod \ p$

증명을 해볼까요? $P \rightarrow \{1, 2, ...,p-1\}$ 과 $X \rightarrow \{a\ mod\ p, 2a\ mod \ p, ...,a(p-1) \ mod \ p\}$가 있습니다. 먼저 증명하고 싶은 것은 $X$의 모든 원소가 서로 다르다는 것입니다. 이를 증명하기 위해 $P$ 에서 서로 다른 $j$와 $k$를 뽑는다면, 이들에 $a$ 를 곱하고 $p$ 로 모듈러 연산한 것은 $X$의 서로 다른 두 원소가 됩니다. 만약 이 두 원소의 값이 같다고 미리 결과를 부정해봅시다. 귀류법을 이용하는 겁니다.

즉, $aj \ mod \ p = ak \ mod \ p$ 입니다. 이를 다시 쓰면 $ja \equiv ka \ (mod \ p)$ 가 됩니다. 근데 여기서 우리는 위에서 배운 특성 중 하나로 $a$ 가 소수인 $p$ 와 서로소이므로 저 식은 $j \equiv k\ (mod \ p)$ 를 만족한다고 표현할 수 있습니다. 그런데 $j$ 와 $k$ 가 모두 $p$ 보다 작은 수로 설정했기 때문에 저 식은 $j =k$ 가 되어버립니다. 모순이 생기는 것이죠. 따라서 모든 원소가 서로 다른 $p-1$ 개의 $p$ 의 나머지들을 원소로 하는 집합 $X$ 는 $P$ 와 동치인 겁니다.

자, 그렇다면 이 원소들을 모든 곱한 것이 같게 됩니다. 즉, $a\ mod\ p\ \times 2a\ mod\ p\ \times ... \times a(p-1)\ mod\ p = 1\ \times 2\ \times .. \times \ (p-1)$ 입니다. 여기서 $P$ 의 원소들은 모두 $p$ 보다 작기 때문에 이 식을 $a\ mod\ p\ \times 2a\ mod\ p\ \times ... \times a(p-1)\ mod\ p = 1\mod \ p \times 2\ mod \ p \times .. \times \ (p-1)\ mod \ p$ 로 쓸 수 있습니다. 양변 전체를 $p$ 로 모듈러 연산 하여 $[a\ mod\ p\ \times 2a\ mod\ p\ \times ... \times a(p-1)\ mod\ p] \equiv [1\mod \ p \times 2\ mod \ p \times .. \times \ (p-1)\ mod \ p] \ mod \ p$ 까지 표현할 수 있습니다.

여기서 우리는 모듈러 연산의 곱셈 특성을 하나 알아야 합니다.

$((a \mod\ N) \times (b \mod\ N)\ mod\ N = (a \times b)\ mod\ N$

간단하게 $a = xN + \alpha$, $b = yN + \beta$ 라고 할 때 적용하면 $(\alpha\beta) \ mod \ N = (xyN^2 + \alpha yN + \beta xN + \alpha\beta) \ mod \ N = (\alpha\beta) \ mod \ N$ 이기 때문입니다. 이를 이용하면 저 위의 식을 간단하게 $[a \times 2a \times ... \times a(p-1)] \equiv [1 \times 2 \times ... \times (p-1)] \ mod \ p$ 로 쓸 수 있으며 이를 계산하면 $a^{p-1}(p-1)! \equiv (p-1)! \ mod \ p$ 이고 양 변에서 $(p-1)!$ 을 제거하면 최종적으로 $a^{p-1} \equiv 1 \ mod \ p$ 를 유도할 수 있습니다.

이렇게 페르마의 정리를 증명할 수 있습니다.

Euler's Phi(Totient) Function(오일러 파이함수)

그 다음으로 알아볼 것은 Euler's Phi(Totient) Function(오일러 파이함수) 입니다. 간단합니다.

오일러 파이함수 $\phi(n)$는 $n$ 보다 작으며 $n$ 과 서로소인 양의 정수의 개수를 의미합니다.

그렇기 때문에 소수 $p$ 에 대해서 $\phi(p) = p - 1$ 이 성립합니다. 이를 기반으로 할 때, 다음과 같은 식이 성립합니다.

서로 다른 두 소수 $p$ 와 $q$ 이며 $n=pq$ 라 할 때, $\phi(n) = \phi(pq) = \phi(p) \times \phi(q) = (p-1)\times(q -1)$

이것 또한 증명을 해볼까요? $n$ 보다 작은 양의 정수는 $P \rightarrow \{1,2,...,(pq-1)\}$ 가 있습니다. $n = pq$ 에서 $p$ 와 $q$ 가 소수 이기 때문에 이 $P$ 에서 $n$ 과 서로소가 아닌 수는 $p$ 의 배수인 $\{p,2p,...,(q-1)p\}$ 로 총 $q-1$ 개이고, $q$ 의 배수인 $\{q,2q,...,(p-1)q\}$ 로 총 $p-1$ 개 입니다. 따라서 $\phi(n)$ 은 $(pq - 1) - (p - 1) - (q - 1) = pq - p - q + 1 = (p-1)(q-1) = \phi(p)\times\phi(q)$ 이 됩니다.

Euler's Theorem(오일러의 정리)

오일러의 정리는 다음과 같습니다.

$a$ 와 $n$ 가 서로소인 양의 정수일 때, $a^{\phi(n)} \equiv 1 \ (mod \ n)$

여기서 $n$ 이 소수인 $p$ 일 때 $a^{p-1} \equiv 1 \ mod \ p$ 과 같은 식이 나옵니다. 페르마의 정리이죠? 맞습니다. 오일러의 정리는 페르마의 정리를 보다 넓은 범주로 확장한 공식입니다. 증명해볼까요?

$n$ 과 서로소인 $n$ 보다 작은 집합 $R = \{x_1, x_2, ...,x_{\phi(n)}\}$ 과 같습니다. $\phi(n)$ 개니까요! $R$ 의 각각의 원소에 $n$ 과 서로소인 $a$ 를 곱하여 $n$ 으로 모듈러 연산을 취한 집합 $S=\{(ax_1mod \ n),(ax_2mod \ n),...,(ax_{\phi(n)} mod \ n)\}$ 와 같습니다. $a$와 $x_i$ 과 모두 $n$ 과 서로소이기 때문에 $ax_i$ 또한 $n$ 과 서로소입니다. 이를 알고 페르마의 정리를 증명했던 매커니즘을 적용하면 똑같이 $R$ 과 $S$ 과 동치임이 밝혀지고 원소들을 모두 곱해 최종적으로 위와 같은 공식이 유도되게 되는 것입니다.

자 이제 오일러의 정리를 통해 $a^m \equiv 1\ (mod \ n)$ 을 만족하는 $m$ 중에 $\phi(n)$ 이 있음을 알게 되었습니다. 하지만 $m$ 을 만족하는 수는 많이 존재합니다. 그 중에 하나가 $\phi(n)$ 일 뿐 인것이죠. 아래 $a$를 7, $n$을 19로 하는 예시를 봅시다.

• $7^1 = 7(mod \ 19)$
• $7^2 = 49 = 11(mod \ 19)$
• $7^3 = 343 = 1(mod \ 19)$
• $7^4 = 7(mod \ 19)$
• $7^5 = 11(mod \ 19)$
• $7^6 = 1(mod \ 19)$

$m$ 에는 3과 6이 있음을 알 수 있습니다. $\phi(19)$는 18인데 벌써 18 전에도 이렇게 나오는 군요. 기억해야 할 것은 $a^m \equiv 1\ (mod \ n)$ 를 만족하는 $m$ 중에 가장 작은 값을 바로 Order 라고 한다는 것입니다. 여기서는 order 가 3이 되겠네요. 아래는 modulo 19 의 예시입니다.

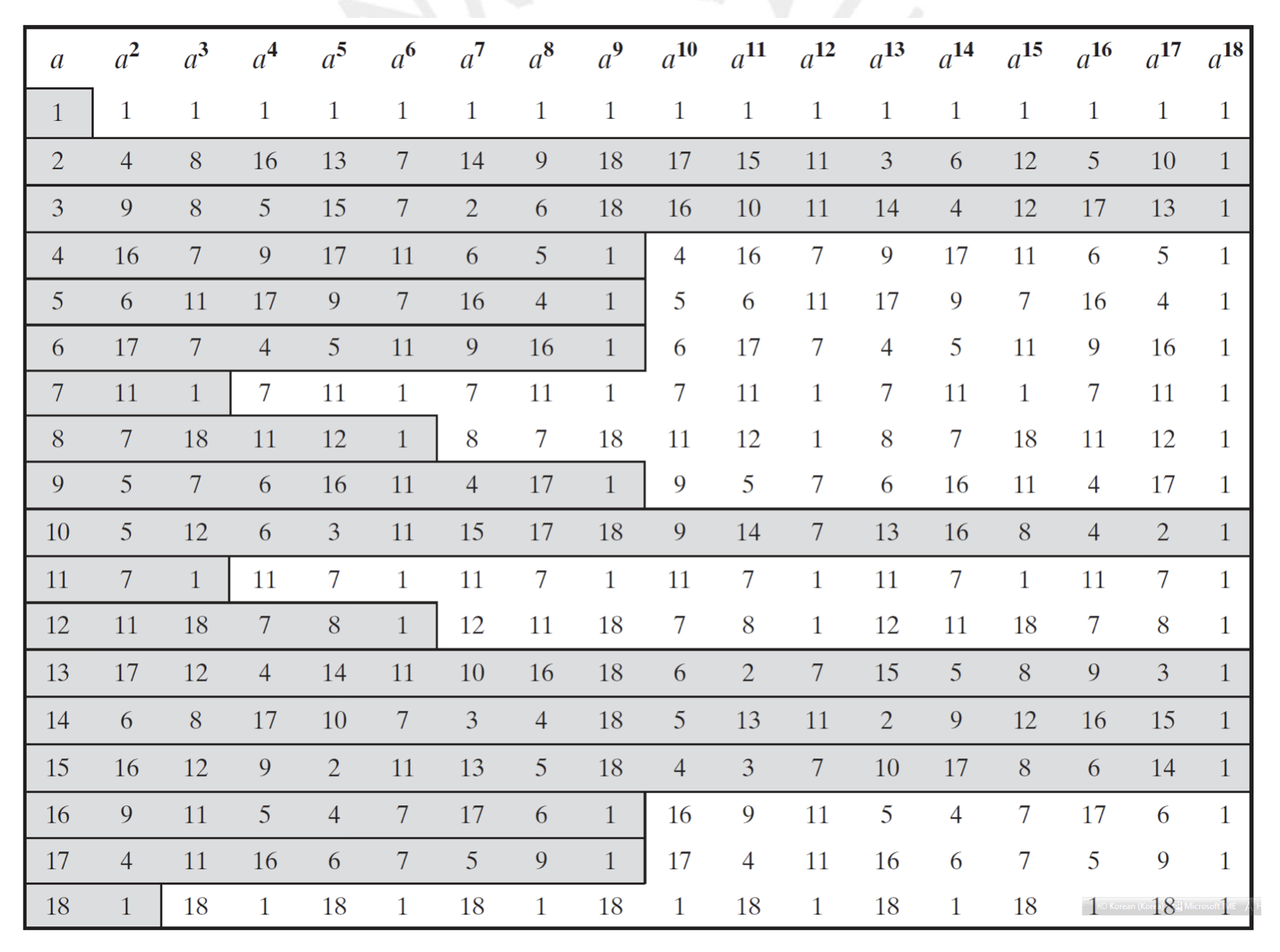
modulo 19 상에서 $a$는 1에서부터 18까지의 정수만이 가능합니다. 모듈러의 곱셈 특성만 봐도 19보다 큰 결과는 어차피 위와 같을 테니까요. 그렇게 보면 1부터 18까지의 modulo 19 상에서의 order 를 알 수 있을 뿐만 아니라 1이 order의 주기 로 반복되는 것을 확인할 수 있습니다.

그런데 만약 어떤 $a$ order 가 오일러 정리에서 사용되었던 $\phi(n)$ 과 같다면 우리는 이 때의 $a$ 를 $n$ 의 Primitive Root(원시근) 이라 부릅니다.

위의 $n$이 19일 때의 예시에서 $\phi(19)$ 는 18이므로 order 가 18인 2, 3, 10, 13, 14, 15가 19의 Primitive Root 가 되는 것이죠. 오일러 정리에 따라 $a$ 는 $n$ 과 서로소인 양의 정수이면 되지 $n$ 이 꼭 소수여야 할 필요는 없습니다. 그러면 $a$ 의 경우의 수가 제일 많을 뿐이지요. 예시로 $n$ 이 14 일 때, $a$ 는 14 와 서로소인 {1, 3, 5, 9, 11, 13} 가 되고, 계산을 해보면 이 중 order 가 $\phi(14) = 6$ 인 원시근은 3과 5 입니다.

또한 원시근은 다음과 같은 특징을 지닙니다.

만약 $a$ 가 $n$ 의 원시근일 때, 그것의 제곱인 $a, a^2, ..., a^{\phi(n)}$은 모두 mod n 상에서 각자 다르며 모두 $n$과 서로소이다.

$n$과 서로소인 $a$의 제곱들이 mod n 에서 $n$과 서로소인 건 당연하겠지만, 제곱들이 모두 다른 것은 정말 신기하지 않나요?

Discrete Logarithm

이제 지금까지 배운 것들을 이용해서 Trapdoor Funciton 을 만들어 봅시다. 먼저 $p$ 를 다른 모두 수들이 서로소가 되도록 소수로 잡습니다. 그리고 양의 정수 $a, b$ 가 있을 때 다음과 같은 식을 세우는 겁니다.

$b \equiv a^i(mod \ p)$

여기서 $i$ 를 찾는 문제를 Discrete Logarithm 문제라고 합니다. $p$는 다 아는 값이고 만약 $a$ 와 $i$ 가 주어졌을 때, $b$ 를 찾는 건 어떨까요? 정말 그대로 연산해서 $b$ 값을 구해보면 될 것입니다. 그런데 만약 역으로 $a$와 $b$ 가 주어지고 $i$ 를 찾으라 한다면요? 만약 $a$ 가 원시근이라면 $i$ 가 달라질 때마다 모듈러 값도 항상 달라지기 때문에 모든 경우의 수를 다 해보는 수밖에 없을 겁니다. 한 쪽은 쉽고 한 쪽은 어려운 것이죠.

$a$ 가 원시근일 경우 $i$ 가 될 수 있는 범위는 $0 \leq i < p$ 이기 때문에 만약 이 $p$ 가 4000 비트에 달할 정도로 무~~~지하게 큰 수라면 $i$ 를 찾는 것은 너무 지치는 방법일 겁니다. 제곱이 쉬운 연산은 아니니까요! 우리가 만약 continous 한 영역에서 이를 수행하면 사실 $i = log_ab$ 로 쉽게 구할 수 있을 겁니다. 하지만 우리가 하는 discrete 한 모듈러 영역에서는 굉장히 빡센 일이 되버리는 겁니다.

Diffie and Hellman

이 Discrete Logarithm 이라는 Trapdoor Funciton 으로 개발한 Asymmetric Alogorithm 으로 Symmetric Key Sharing을 도모한 사람이 바로 Diffie 와 Hellman 입니다.

Public Key Distribution 을 도입한 것이죠. 이제 본격적으로 Diffie-Hellman 알고리즘을 살펴보도록 하겠습니다.

사용자로는 다시 한 번 Alice와 Bob을 설정하겠습니다.😁 둘은 global 한 변수인 $a$ 와 $p$ 값을 오픈합니다. 여기서 당연히 $p$ 는 매우매우 큰 소수이고 $a$ 는 이 $p$ 의 primitive root 인 것이죠. 그 다음 각각은 랜덤을 이용해서 자신만의 secret(private) key 를 생성합니다. $p$ 보다 작은 각각 $X_A$ 와 $X_B$ 를 생성한 것이죠. 그리고 이를 이용해서 각각 public key 로 $Y_A = a^{X_A} \ mod \ p$, $Y_B = a^{X_B} \ mod \ p$ 를 생성합니다. 그리고 이 값을 공유합니다. 어차피 풀기 힘든 public 값이기 때문에 굳이 안전한 채널일 필요도 없죠.

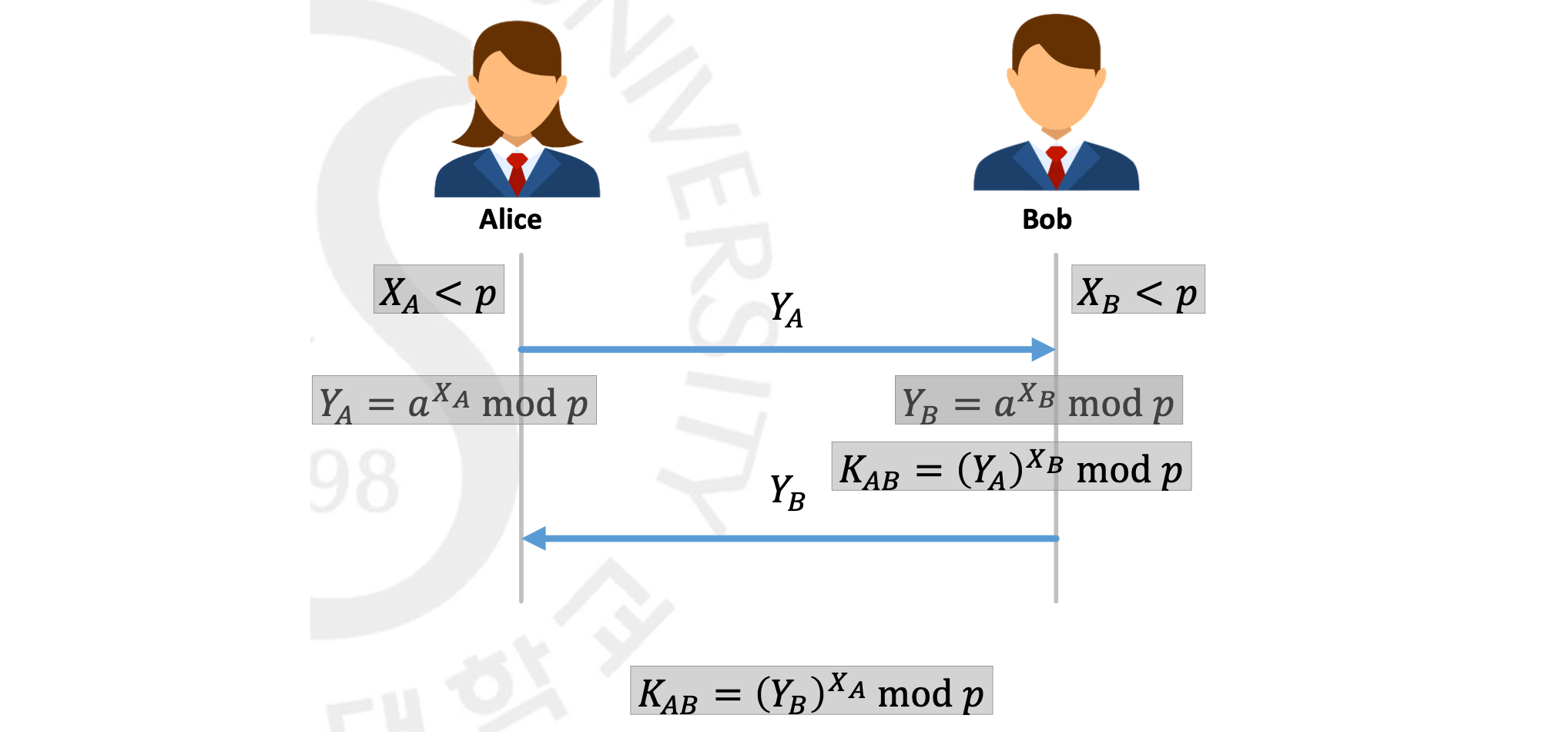
그러면 Bob은 받은 $Y_A$ 를 이용해서 $(Y_A)^{X_B} \ mod \ p$ 를 구하고 Alice 는 받은 $Y_B$ 를 이용해서 $(Y_B)^{X_A} \ mod \ p$ 를 구하는 데 계산해보면 이 값을 둘 다 $a^{X_AX_B} \ mod \ p$ 로 같습니다. 이 값을 $K_{AB}$ 라고 하죠. 이 값은 둘만이 아는 값이기 때문에 session key 로써 활용하는 것입니다.

공격자가 아무리 $a, b, Y_A, Y_B$ 를 안다고 쳐도 진짜 private key 인 $X_A, X_B$ 를 알기 위해서는 하드를 훔치는 게 아닌 이상 필연적으로 Discrete Logarithm 에 직면할 수밖에 없는 겁니다.😂

하지만 재차 얘기하듯이 $p$ 를 아주 크게 잡아버리면 Discrete Logarithm 은 거의 풀 수가 없습니다. 거기에다가 실제로는 비밀키 $X$ 를 약 30분마다 바꾸기 때문에, 설령 푼다해도 30분만에 풀지 못하면 아무 소용도 없게 되는 겁니다. 그래서 일부 공격자들은 미리 트래픽을 다 저장해놓고 있다는 썰도 있습니다. 시간이 지나면 계속해서 컴퓨터는 빨라지기 때문에 언젠가 풀리게 됬을 때 과거의 암호들을 풀 수도 있게 되니까요.

그러나 이러한 방식도 보안에서 가장 취약한 공격 중 하나인 Man In The Middle Attack 에는 약합니다. 아래를 보시죠.

Man In The Middle(MITM)

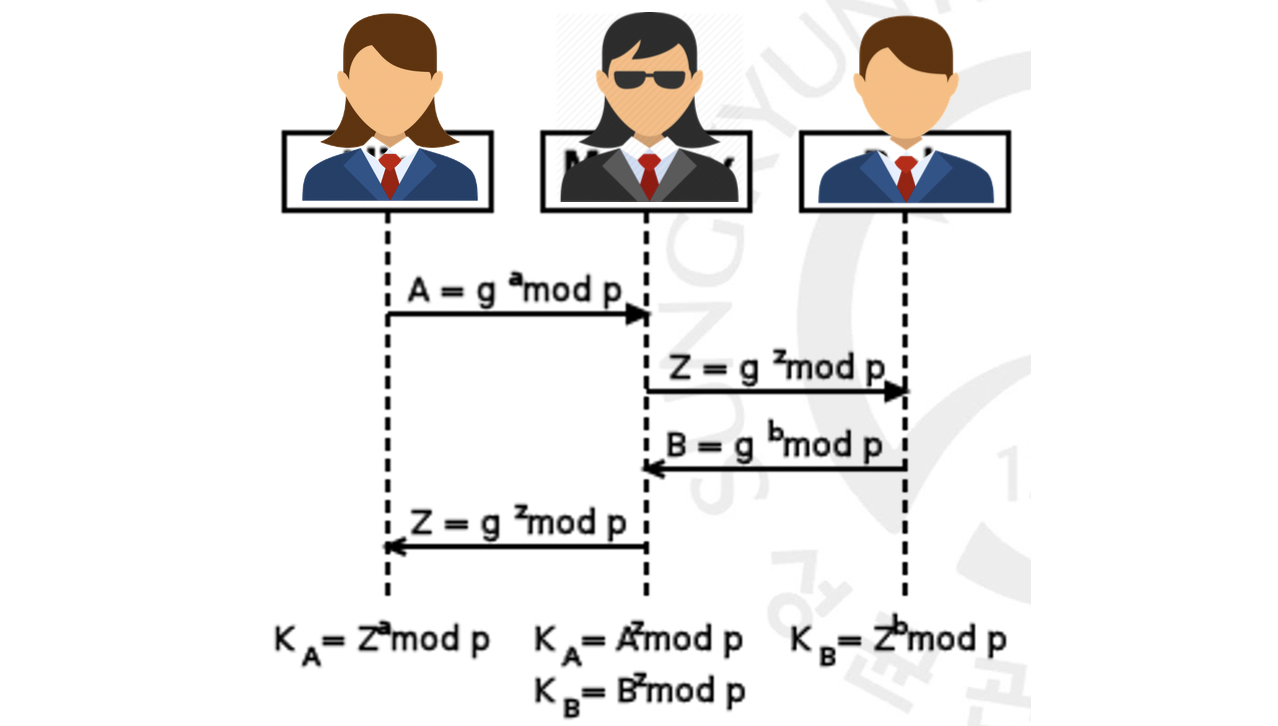
(위 그림에서 $a$ 와 $b$ 는 각각 기존의 $X_A$ 와 $X_B$ 를 의미하며, 마찬가지로 $A$ 와 $B$ 는 $Y_A$ 와 $Y_B$ 를 의미합니다.)
기존에 서로 $Y_A, Y_B$ 를 공유하는 과정에서 공격자가 중간에 껴서 이를 자신도 아는 값인 $Y_Z$ 로 변조하여 보내는 것입니다. 공격자를 중심으로 왼쪽과 오른쪽을 나누어서 봅시다. 이렇게 되면 Alice와 Bob이 비밀값 $K_{AB}$ 를 만드는 것이 아니라 Alice와 공격자가 $K_A = Z^amod\ p = A^zmod\ p$ 를 만들고 Bob 과 공격자가 서로 $K_B = Z^bmod\ p = B^zmod \ p$ 를 만드는 것이 되버립니다. 이러면 공격자가 각각 Alice와 Bob의 암호문을 열어볼 수가 있게 되는 것이죠!😱

이 Man In the Middle 의 원인은 무엇일까요? Alice와 Bob이 서로 모르는 사람이기 때문에 그런 겁니다. Alice는 상대가 Bob 인지를 모르고 마찬가지로 Bob도 상대가 Alice 인지에 대한 확신이 없는 것이죠. 그래서 Authentication(인증) 이 중요한 겁니다!

key 의 주인에 대한 인증이 필요합니다. Alice와 Bob은 서로 인증된 상태에서 public key 를 안전한 방식으로 교환해야 합니다. 그래서 Alice와 Bob 이 서로 신뢰하는 기관(제 3자, Trusted Third Party(TTP)) 에서 받은 인증서로 나의 public key를 입증할 수 있는 겁니다.

Prime Factorization

부록처럼 다른 Trapdoor Function 도 하나 알아보면서 마무리를 할 텐데 그건 바로 Prime Factorization(소인수 분해) 입니다. 우리에게 소수 $p$ 와 $q$ 가 있을 때 이 둘을 곱하여서 $n = p \times q$ 를 만드는 건 너무나 쉽습니다. 그러나 $n$ 을 인수분해하여 $p$ 와 $q$ 를 구하는 것은 무지 어렵다는 겁니다. $p$ 를 무지하게 크게 만들면 최소 $\frac{p}{2}$ 만큼 전수조사를 해봐야 하기 때문이죠.

Asymmetric Cipher - RSA

Symmetric 한 방식이 private-key scheme 이고 Asymmetric 한 방식은 public-key scheme 임을 이제 아실 겁니다. Asymmetric Cipher 의 대표 주자 격이 바로 RSA 입니다. 1977년 MIT 교수인 Rivest, Shamir, Adleman 이 만든 회사로 그래서 이름이 RSA 인 겁니다. 2048비트 이상의 3-400 자리 아주 큰 정수에서의 소수로 방금 설명한 Prime Factorization 을 이용합니다. 셋업을 살펴 보시죠.

먼저 랜덤으로 아주 큰 소수인 $p$ 와 $q$ 를 만들어 둘을 곱한 $n = p\times q$ 를 만듭니다. 그 다음 Euler's Phi(Totient) Function 으로 $\phi(n) = (p-1)(q-1)$ 으로 $\phi(n)$ 을 구합니다. 이는 본인만이 알아야 하는 값이며 $n$은 공개합니다. $n$ 을 알고 있다 하더라도 $\phi(n)$은 $n$ 을 소인수 분해 해야되기 때문에 무지하게 어려운 것이죠.

그 다음 encyption key 인 $e$ 값을 고릅니다. 이 $e$ 값의 조건은 먼저 $1 < e < \phi(n)$ 으로 1과 $\phi(n)$ 의 중간 정도에 있는 값이 적당합니다. 그리고 $gcd(e, \phi(n)) = 1$ 이어야 하는데 이는 Euclidean 으로 쉽게 풀 수 있는 문제이죠. $n$ 과 마찬가지로 $e$ 도 공개를 하는 public 값이 됩니다.

그 다음 decryption key 인 $d$ 값을 구합니다. $d$ 의 조건은 먼저 $0 \leq d$ 이고 $ed = 1\ mod\ \phi(n)$ 으로 바로 $e$ 의 곱셈의 역원, 즉 multiplicative inverse 입니다. 자 근데 여기서 $e$ 알고 $n$ 알아도 소인수 분해를 해야 알 수 있는 $\phi(n)$ 을 구할 수 없기 때문에 마찬가지로 $d$ 또한 구하지 못하는 것입니다. 이런 RSA 는 현재에도 활발히, 특히 비트코인에서도 사용되고 있습니다. 이제 과정을 살펴봅시다.

먼저 상대방이 보내고 싶은 $M$ 이 있을 때 암호문 $C$ 는 public key 인 $e, n$ 을 활용하여 단순 $C=M^e\ mod \ n$ 으로 나타낼 수 있습니다. 물론 $M$ 에 $e$ 승을 구하는 것이 쉬운 일은 아니지만요... 그 다음에 복호화는 private key 인 $d$ 를 활용하여 단순 $M=C^d\ mod \ n$ 으로 나타낼 수 있습니다.

상대방이 보낸 메시지는 오직 나만이 복호화 할 수 있는 것이죠.

그런데 여기에는 $0 \leq M < n$ 이라는 조건이 있습니다. 왜냐면 복호화를 보시면 $M$ 은 $C^d$ 를 모듈로 $n$ 함으로써 구하기 때문입니다. 절대 $n$ 보다 커서는 안되는 것이죠. 근데 처음에 언급했듯이 예전에는 $n$ 에 2048비트가 사용됬습니다.(요즘은 4096이지만요...). 이는 $2^{2048}$ = 617 바이트를 이용하기 때문에 영어를 기준으로 메시지는 617자 까지 밖에 암호화할 수 없는 것입니다. 무슨 1MB도 훨씬 안되는군요! 게다가 symmetric key 에 비해 10 배가 넘는 CPU processing time 이 걸립니다.

그래서 이러한 RSA와 같은 Asymmetric 은 실제로 데이터 자체를 암호화하는 데 사용하기에는 굉장치 적절치 않습니다. 키만 공유가 잘된다면 Symmetric 이 훨씬 좋으니까요. 그래서 Asymmetric 은 Symmetric 을 위한 비밀키를 공유하는 데에 사용이 되어 이 둘을 적절히 혼합하여 사용한답니다.

이 RSA 에서 위와 같은 복호화가 가능한 것은 바로 이전에 공부하였던 Euler's Theorem 덕분입니다. 다시 상기하자면 $a$ 와 $n$ 이 서로소인 양의 정수일 때 $a^{\phi(n)} \ mod \ n \equiv 1$ 이 가능하다는 것이죠. 이 때 $n = p \times q$ 이기 때문에 $\phi(n) = (p-1)(q-1)$ 이 되고요. 그리고 우리가 $d$ 를 $mod \ \phi(n)$ 상에서 $e$ 의 곱셈의 역원으로 구했기 때문에 $ed = 1 + k\phi(n)$ 이 성립합니다. 이 상태에서 보면 모듈로 연산의 특성 중 exponentiation 때문에 $C^d \equiv M^{ed} \ mod \ n$ 가 성립됩니다. 이를 쭉쭉 계산해 보면 $M^{ed} \equiv M^{1+k\phi(n)} \equiv M(M^{\phi(n)})^k mod n$ 가 됩니다. 그런데 여기서 $M$ 이 $n$ 과 서로소라면 이 식은 최종적으로$M(1)^k\equiv M mod \ n$ 이 되기 때문에 이와 같이 복호화가 가능한 것입니다. 실제로 $n = p\times q$ 이기 때문에 $M$ 이 서로소가 안되려면 $p$ 나 $q$ 의 배수여야 하는데 $n$ 이 매우 크면 이럴 확률도 매우 적습니다.

정리하자면, $n$ 과 $e$ 는 public key 이고, $d$ 는 private key 입니다. 유념해야 할 것은 $d$ 를 구할 수 있는 $\phi(n)$ 은 절대 공개하면 안된다는 겁니다!😤

그래서 우리는 결과적으로 $n$ 은 어떻게 구할까요? $n$ 을 구하려면 먼저 소수인 $p$ 와 $q$ 를 구해야 합니다. 따라서 $p$ 보다 작은 큰 값을 정하고 이것이 소수인지를 판단하기 위해 Fermat's little Theorem 을 사용합니다. 다시 상기하자면 $p$ 가 소수라면 $a^{p-1}\ mod \ p =1$ 이라는 것인데 $p$ 가 소수가 아닌 경우라도 이를 만족할 수는 있는 것이기 때문에 $p$ 가 소수가 아닌 것만 정확히 판별할 수 있는 한계를 지닙니다. 따라서 한 8번 정도 페르마의 정리로 테스트로 해서 통과를 하면 그냥 그 값을 택합니다. 아쉽게도 이 외에 다른 방법은 아직 없습니다...🥲

결론적으로, RSA는 훌륭하지만 크기의 한계가 명확하게 드러나있기 때문에, 실제로 어떤 데이터를 암호화할 때는 아래와 같은 순서로 진행합니다.

1. 랜덤으로 256비트의 keystring $K$ 를 구합니다.
2. 데이터를 AES 와 CBC 를 $K$ 를 이용해 암호화 합니다.
3. $K$ 값을 RSA 를 이용해서 암호화 합니다.
4. 이 두 값을 모두 상대에게 보냅니다.

이렇게 나만 풀어볼 수 있는 RSA 를 통해서 우리는 Diffie-Hellman 과 마찬가지로 Symmetric Cipher 를 위한 secret key 공유를 할 수 있습니다. 물론 이도 마찬가지로 Man In The Middle 공격을 받을 수 있습니다. 암호화 하기 위해 쓰는 public key 가 정말 상대방의 것인지 확신이 없기 때문입니다. 이를 위해 서로가 신뢰하는 Trusted Third Party(TTP) 를 통해 public key 에 대한 Authentication(인증) 이 필수라는 것은 잊지 마시기 바랍니다.

이를 위해 RSA 를 Digital Signature(디지털 서명) 으로도 사용할 수 있습니다. 서명은 자신을 증명하는 것으로 남들이 절대 위조를 하지 못하야 하는 것이 목적입니다. 그래서 나만의 private key 로 암호화를 하면 public key 를 가진 모든 사람이 복호화를 함으로써 증빙을 할 수 있게 됩니다. 내 private key 를 모른다면 그 누구도 해당 public key 로 풀리는 암호문을 만들 수가 없을테니까요! RSA 에서 암호화는 $C=M^e\ mod \ n$ 이고, $M=C^d\ mod \ n$ 인데 여기서 기존과 달리 $e$ 를 private key 로 하고 $d$ 를 public key 로 하면 되는 것이죠. 정리하자면, 나를 증명하기 위해 제 3자가 Authentication 해주는 과정에서 Digital Signature 가 쓰이는 것이지요.

결론적으로 이번에 공부한 Asymmetric 방식은 자신만의 key 가 외부에 노출될 위험이 현저히 적기 때문에 Symmteric 의 취약점을 보안할 수 있는 겁니다.