
여러분들 혹시 파노라마 사진을 찍어본 경험이 있나요? 옆으로 돌면서 사진을 차례차례 찍으면 나중에 그 사진이 이어져 하나의 긴 전경이 되는 것을 확인할 수 있습니다. 이런 식으로 수평정적으로 길게 이어진 전경의 이미지를 Panorama 라고 합니다. 이러한 파노라마 사진은 넓은 각도를 가지는 렌즈를 가지는 카메라로 찍을 수도 있지만, 그렇지 못한다면 여러 장의 사진을 이어 붙이는 것으로 만들 수 있겠지요.
이렇게 이미지를 이어 붙이는 것을 Iamge Stiching 이라고 합니다. 그러면 저희가 아래와 같은 여러 장의 이미지들을 찍었다고 생각해 봅시다.

이 이미지들을 정말 순서에 맞게 그대로 가져다가 이어 붙인다면 어떠한 결과가 나올까요? 중간의 계단 부분만 붙여 봅시다.

위와 같이 중앙 오른쪽을 보면 맞물려 있지 않고 엇갈려 있어 부자연스러운 느낌을 받을 수 있습니다. 우리가 붙인 두 사진의 각도가 다르기 때문입니다. 실제로 우리가 이 이미지를 찍었을 때 눈으로 봤던 것과 같은 넓은 전경을 가지기 위해서는 각도를 맞춰주어야 합니다. 이때 사용되는 것이 바로 오늘 공부할 Image Homographies 입니다.

Homographies 를 이용해 각도를 맞춘다는 것을 조금 더 명시적으로 느끼기 위해 아래의 그림을 첨부하겠습니다.

평면의 각도를 변환하는 Homography 는 아래와 같이 사용될 수도 있습니다.

서로 같은 곳에서 다른 각도로 찍은 두 건물을 같은 방향으로 돌려 팽행하게 정렬시켜 줄 수도 있습니다. 이를 Image Rectification 이라고 합니다.
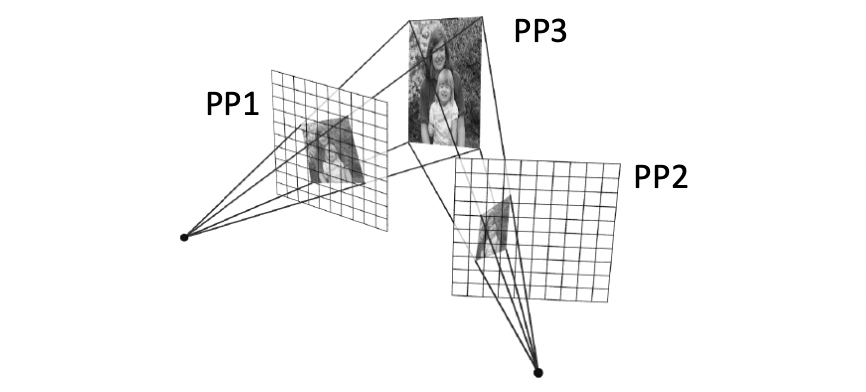
Homography 의 기본적인 아이디어는 위와 같습니다. PP3 라는 사진의 평면을 서로 다른 방향에서 보고 있다, 아니 찍었다고 하죠. 서로 다른 지점에서 보고 있는 방향을 나타내는 벡터를 법선벡터로 가지는 평면이 있겠지요? 간단히 상상해보면 향하고 있는 방향에 평행한 평면 PP1, PP2 가 있을 겁니다. 그러면 해당 지점에서 찍은 사진은 평면 원본 사진 PP3 를 각 평면 PP1, PP2 에 Project 한 평면일 것입니다.
잠깐 평면의 Project 라고요? 바로 이전 글에서 공부하였던 2D Transformations 를 상기해 봅시다.
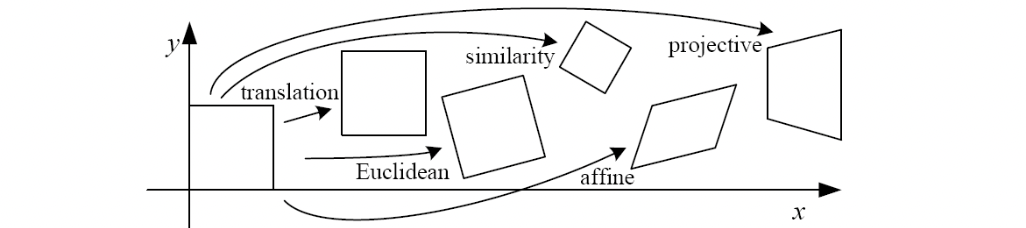
맞습니다. Homography 는 바로 Projective Transformation 을 의미하는 것입니다.

다른 어떤 Transformation 보다 projective transformation, 즉 Homography 로 했을 때 stiching 이 가장 잘 되는 것을 확인할 수 있습니다.

homography 평면 정보를 알기만 한다면 위와 같이 projective transformation 을 이용해서 뷰를 옮길 수도 있습니다. View Warping 을 하는 것인데요. 원본에서 밑부분 바닥 부분을 늘리고 각을 맞추면 위에서 본 가운데 이미지처럼 되지 않겠어요?
그러나 이런 Homography 도 언제나 사용할 수 있는 건 아니구요. 총 세 가지 조건이 있습니다.

- 피사체가 평면입니다.
Homography 는 무조건 평면을 대상으로 합니다. 애초에 2D Transformation 이니까요.

- 피사체(장면)이 평면에 가까워야 합니다.
만약 평면이 아니라면 적어도 평면에 가까워야 합니다. 왜냐하면 실제로 평면이 아니라도 우리는 평면이라 가정하여, 즉 평면화 시켜서 생각할 것이기 때문입니다. 그래서 어떤 장면에 여러 물체들이 있다면 그것들의 Depth 가 아예 가깝거나 멀어야 합니다.
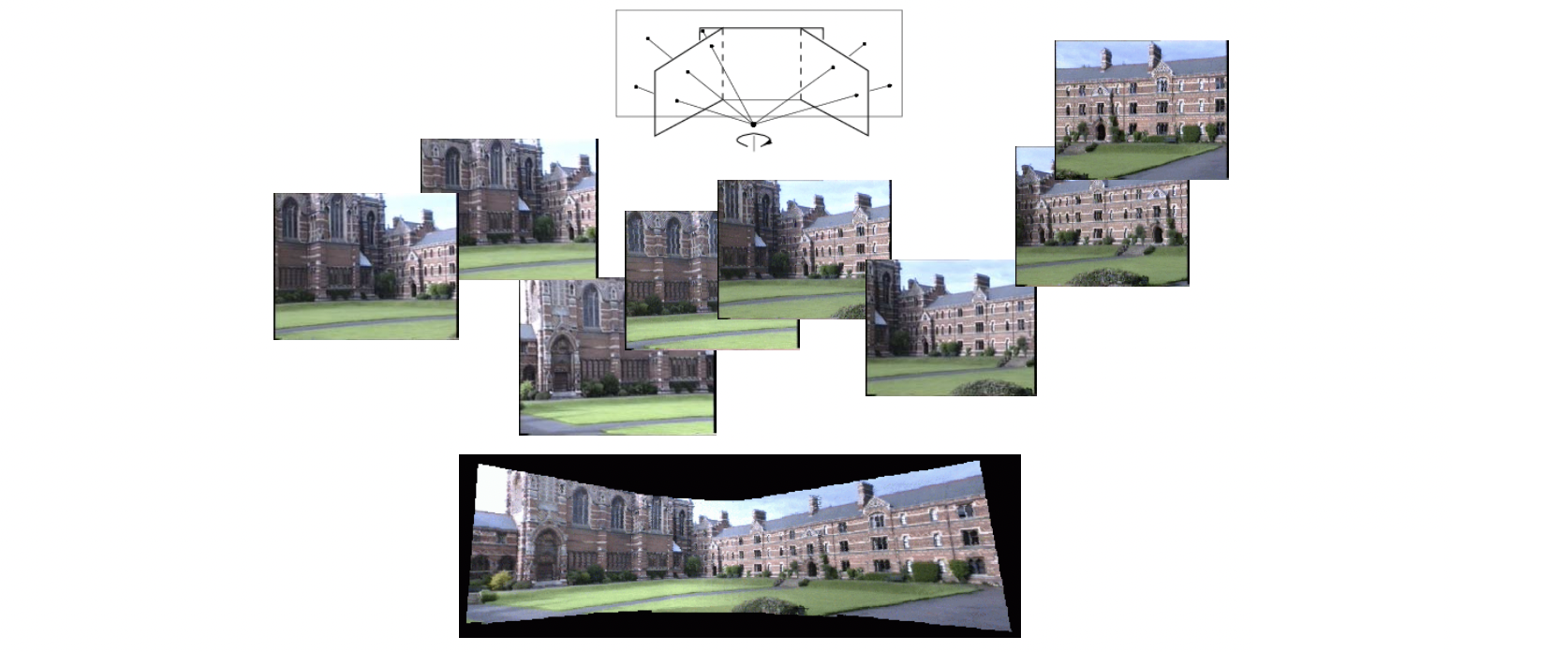
- Tranformation 하는 두 이미지는 같은 중앙에서 찍은 것이어야 합니다.
카메라는 위치를 움직이지 않고 오직 회전만 한 것이어야 합니다. 왜인지는 위를 보다시피 이 원리를 그림으로 표현한 것을 보면 알 수 있습니다. 파노라마는 한 장소에서 서로 다른 각도로 인해 서로 다른 평면들을 뒤에 굉장히 큰 평면이 있다고 가정하여 이 곳에 Project 시키는 것입니다.
Determining a Homography
이제 서로 다른 두 이미지 사이의 Homograpy(Projective Transformation) 를 결정해 봅시다. 이미 다 한 내용입니다.
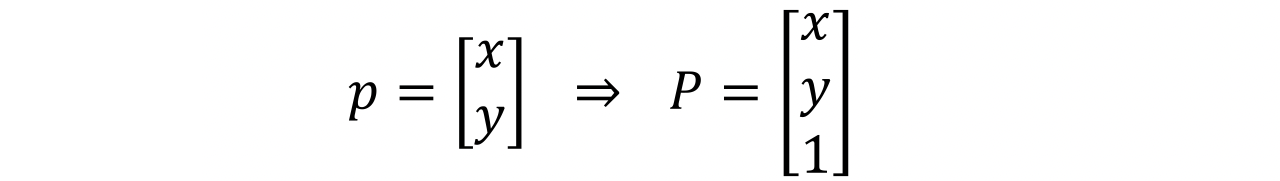
먼저 2 차원 상에서의 위치 좌표 를 homogeneous coordinates 로 바꾼 를 사용할 겁니다. 그리고 나서 매칭되는 feature 의 좌표 가 있음을 전제로 합니다. 이 매칭 관계를 이용해서 우리는 두 이미지의 Homography 를 구하고 싶은 겁니다.

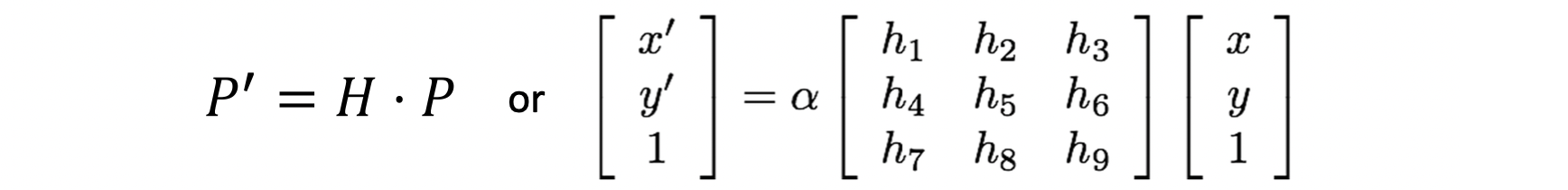
변경되어야 할 좌표 를 찾는 것은 오직 위와 같이 Transformation Matrix 와 곱하는 것 뿐입니다. 이 matrix 는 언급했다 시피 Projective(Homography) Matrix 입니다. 는 homogenous 상에서는 scale invariance 하기 때문에 벡터의 마지막 값을 1로 맞처주기 위해 곱하여진 상수겠구요. 계산해볼까요?
이며 여기서 마지막 식이 1 임을 이용해 위 두 식의 좌향에 곱해주면
이를 재정렬 하면 최종적으로 아래와 같은 식이 나오는데요.
이 식은 아래와 같은 matrix 의 곱으로 표현할 수 있습니다!
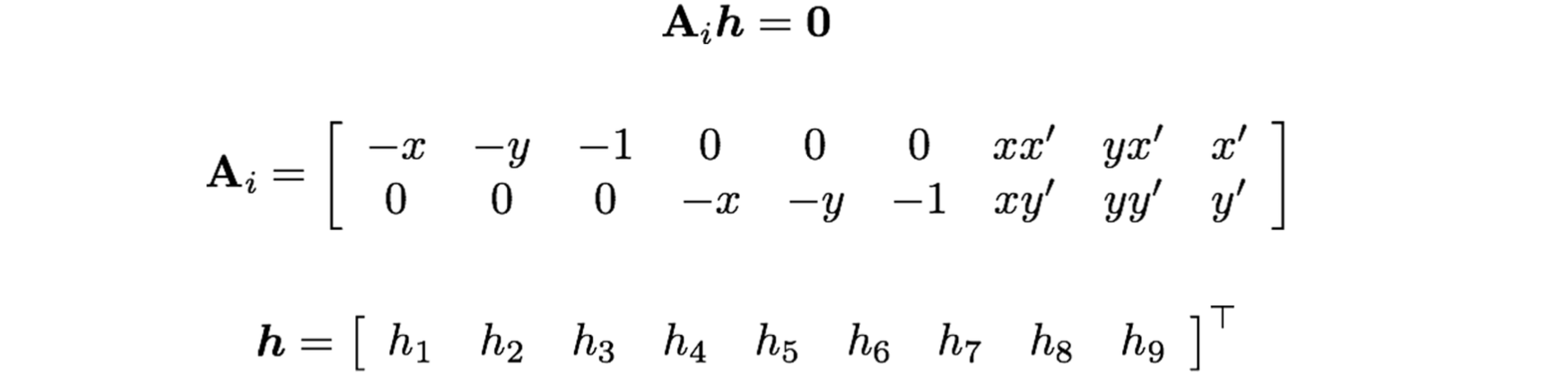
그런데 이러한 feature 매칭들은 한 두 개가 아니겠지요? 그래서 이를 담고 있는 matrix 에 이 값들을 쌓아 matrix 를 키우는 겁니다. 아래처럼요.

매칭 데이터 하나로는 식이 2개 나옵니다. 그런데 이미 아시다시피 Homography Matrix 의 자유도, 즉 우리가 구해야 할 미지수의 개수는 8개 입니다. 그렇기 때문에 우리는 를 정의하기 위해선 최소 4 개 이상의 데이터가 필요합니다. 이보다 적은 것을 underconstraint 라 하며 이 때 우리는 를 정의하는 것이 불가능합니다. 딱 4개라면 값이 완전이 이 4개의 데이터에 최적화되어서 결과가 나올 것이구요. 만약 4 개를 넘는다면 overconstraint 로 이 때는 최대한 이 데이터들에 부합되는 를 찾아야 할 것입니다. 일반적으로는 이 overconstraint 상황이 유력합니다. 아무리 못해도 특징점 매칭이 4 개는 넘을 것이고 그리고 많으면 많을 수록 결국 전체적으로 정확한 homography 를 구할 수 있을 테니까요.
이러한 문제를 Linear Least Squares Problem 이라 하며 Singular Value Decomposition(SVD) 로 풀 수 있습니다. 를 SVD 한 결과는 아래와 같습니다.
여기서 의 크기가 이라 했을 때 는 크기의 orthonormal matrix 이고, 은 크기의 diagonal matrix, 마지막으로 는 크기의 orthonormal matrix 입니다. 이렇게 하면 신기하게도 의 열 벡터는 의 해가 됩니다. 그리고 번째 열 벡터일 때 해당되는 오류 값이 바로 matrix 의 번째 값 (diagonal 이라 열에 값은 하나이므로) 이 되는 겁니다. 그래서 에서 0 이 아닌 (이러면 해도 영벡터가 되버리기 때문에) 가장 작은 값에 해당하는 열이 번째 열이라면 의 번째 열이 우리가 최종적으로 찾고자 하는 벡터가 되는 것입니다. 왜 그런지는 선형대수학에 대하여 해당 부분을 공부하시기 바랍니다.😉
Feature-based Alignment
앞에서 Homography 를 구한다는 것은 결국 매칭되는 feature 들을 전제로 하였습니다. 그렇다면 과연 이 feature 들은 어떻게 매핑을 시킬 수 있을까요? 이 예시에서는 우리가 transformation matrix 로 Projective matrix 를 가정한 것으로 시작해봅시다.

일단 가장 먼저 할 것은 당연하게도 feature extraction(detection + description) 입니다. 저번 글에서 설명드린 SIFT 같은 것들을 쓰면 되겠지요? 위의 이미지를 보시면 우리 눈으로는 왼쪽 이미지의 오른쪽과 오른쪽 이미지의 왼쪽 부분이 다른 각으로 겹치는 것을 확인할 수 있습니다. 그런데 컴퓨터가 이에 대한 매핑 관계를 찾아내기 위해서는 어떻게 해야 할까요?

먼저 모든 feature 들의 매핑 관계를 지어봐야 합니다. 왼쪽의 feature 의 수가 개 이고, 오른쪽이 개라면 총 개의 feature 매칭들이 생기게 됩니다.

이 중에서 feature 들의 Similarity(유사도) 를 판단하여 가장 상위의 5% (예시 - 디자인 초이스) 만 남깁니다. 남은 매치들을 Potential Matches 라 합니다. 유사도를 판단하는 방법은 히스토그램을 비교하는 등 여러 가지가 있겠지요? 개발자가 선택하기 나름, 즉 디자인 초이스 중 하나가 됩니다.

그 다음, 할 것은 Verify(검증) 과정입니다. 남은 매칭 관계들 중에서 4 개를 랜덤으로 고릅니다. 그러면 이 4개를 가지고 Transformation matrix 를 구할 수 있게 됩니다. 그런데 이 4개의 매칭 관계가 정확해야 homography 도 정확한데 랜덤으로 고른 거라 이를 알 수 없습니다. 그래서 검증이 필요합니다. 이 구한 로 남은 매칭들의 오류를 구해보는 겁니다. 시간이 될 때까지 이를 반복한 뒤, 최종적으로 오류가 가장 적은 를 선정합니다.

이렇게 Homography 까지 구할 수 있는 것이죠.
그런데 문제는 우리가 앞선 과정에서 Similarity 를 판단할 때 오직 비주얼적인 것으로만 판단하게 되기 때문에 굉장히 모호한 매치들이 생겨날 수 있다는 겁니다. 예를 들어 아래 그림을 봅시다.

울타리 위에 튀어나온 부분을 feature extraction 했습니다. 그런데 문제는 이렇게 생긴 부분이 오른쪽 이미지에서도 많아서 이 뿐만 아니라 다른 많은 feature 과의 유사도가 너무 높게 나올 수 있다는 것입니다. 우리는 직관적으로 오른쪽 이미지에서도 같은 위치의 feature 와 매칭되야 된다는 걸 알지만 시각적인 것으로만 판단하는 컴퓨터는 이와 같은 오류를 범할 수 있다는 것이지요.
이와 같은 문제를 해결하기 위해, 즉 올바른 feature matching 을 찾기 위해 우리는 RANSAC(RANdom SAmple Consensus) 을 활용할 것입니다. 사실 방금 Homography 를 구하는 과정을 살짝 확장한 것인데요. 마찬가지로 transformation matrix 로 homography 를 가정하고 시작했다고 합시다. 그러면 랜덤으로 4 개의 매치를 골라 를 구합니다. 그 다음 나머지 매칭들 하나하나에 대하여 해당 에 대한 오류 값을 구한 뒤, 특정 threshold 보다 작은 inlier 들의 개수가 얼마나 되는지를 세는 겁니다. 이를 시간이 허락하는 한 최대한 반복해서 inliner 의 수가 가장 많은 를 고르는 것이지요.

헤매고 있었는데 정리가 잘 되어있어서 도움이 많이 되었습니다. 좋은글 감사합니다!