컴퓨터 비전에 맨 첫 번째 Image Filtering 을 설명하는 글에서 아래와 같은 사진을 보였습니다.
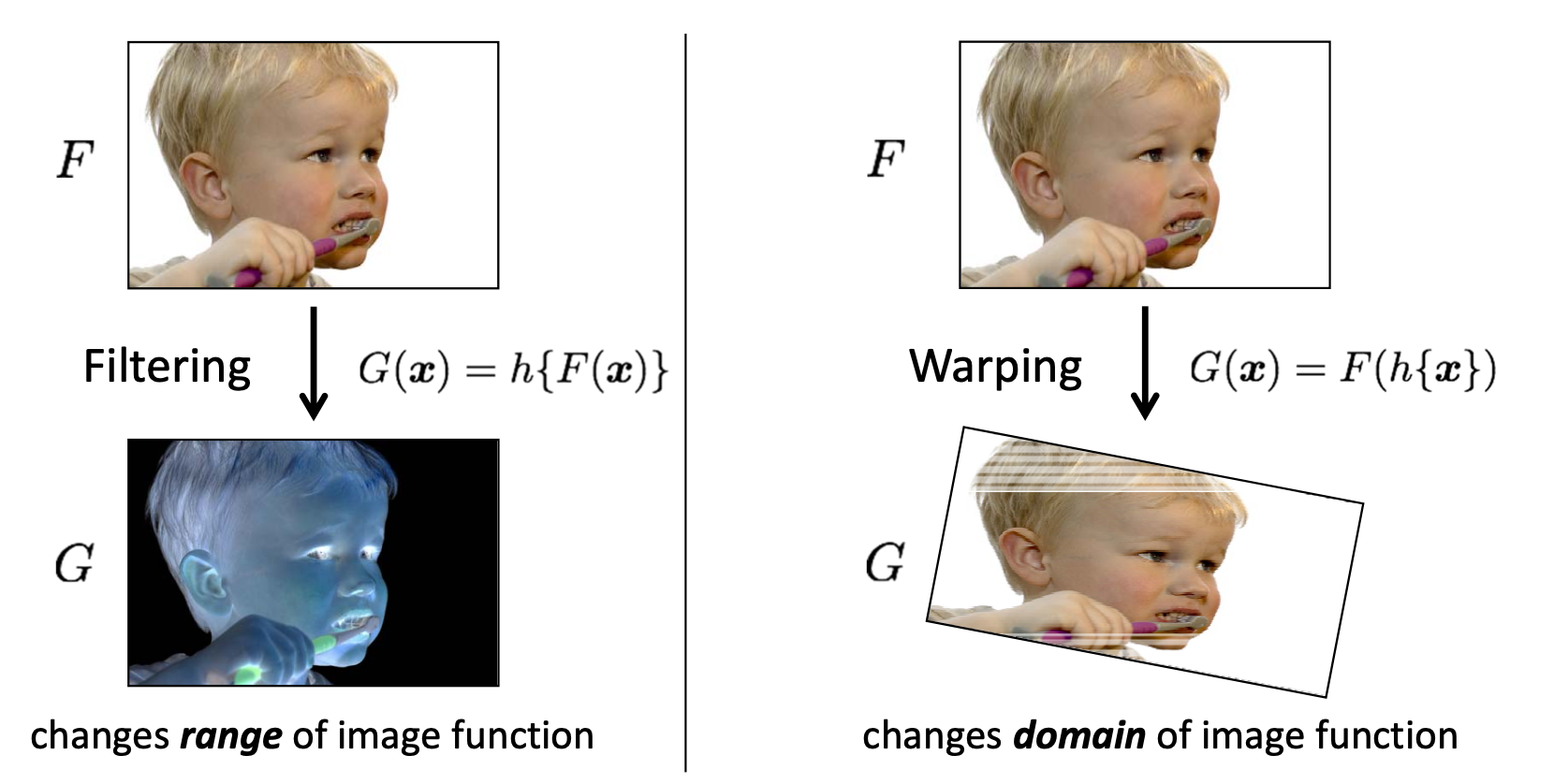
다시 정리하자면, 값을 변화시키는 함수를 로, 이미지를 라고 했을 때 Filtering 은 이미지 픽셀 값들에 를 적용하는 것입니다. 예를 들어, 라고 한다면 2 배가 밝아진 이미지가 되겠네요. 이를 이미지 함수의 Range 를 변경한다고 표현합니다. 그리고 Warping 은 좌표에 를 적용하는 것이기 때문에 똑같이 라면 반이 줄은 이미지가 되겠군요. 이를 이미지 함수의 Domain 을 변경한다고 표현합니다. 이번에 다룰 내용은 바로 이 Warping 에 관한 내용입니다.

위와 같이 서로 다른 이미지 와 에 대하여 feature matching 을 진행한 결과입니다. 매칭된 부분들끼리는 3차원 공간 상에서 같은 점에 해당되는 것이지요. 즉, 우리가 알고 있는 것은 , , 그리고 매칭 정보로 이것들을 이용해서 어떻게 의 를 구할 수 있는 것인지를 얘기해보려 합니다.
매칭되는 두 점을 각각 와 라고 할 때 우리는 transformation function 인 를
로 정의할 수 있습니다. 여기서 는 함수 의 parameter 입니다. 예를 들어 를 quadratic 모델이라고 했을 때 하나의 모델인 가 되고 여기서 가 가 되는 것이지요. 우리의 목적은 매칭 관계에 가장 잘 부합하는 의 추정치를 찾는 것입니다.
2D Transformations
다시 말하자면 2D Transformations 는 Image Warping 을 의미하는 것입니다. 아래와 같이 다양한 종류의 2D Transformation 이 존재합니다.

당연히 input 은 2D 이미지이고 output 또한 2D 이미지인 것이지요. 우리는 먼저 2D 공간 자체에서 일어나는 2D Planar Transformations 를 살펴보도록 하겠습니다.
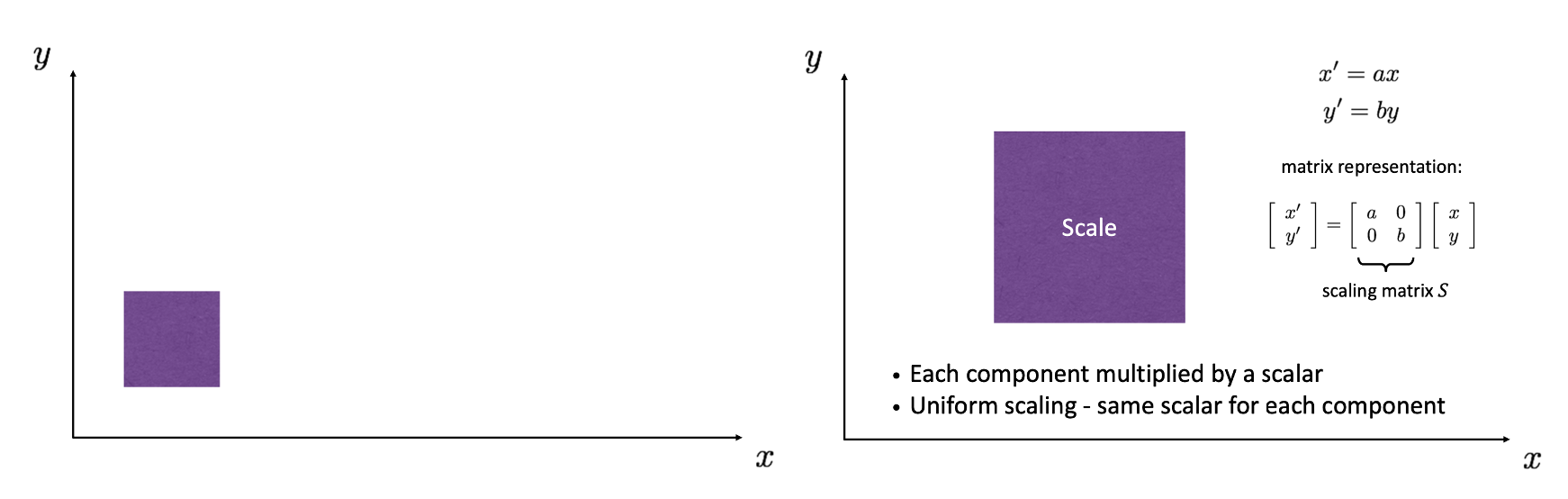
예를 들어 왼쪽의 도형 이미지를 오른쪽과 같이 가로로 배, 세로로 배 키우고, 즉 Scaling 하고 싶을 때는 와 를 적용하면 됩니다. 이를 벡터로 다시 쓰면 가 됩니다.
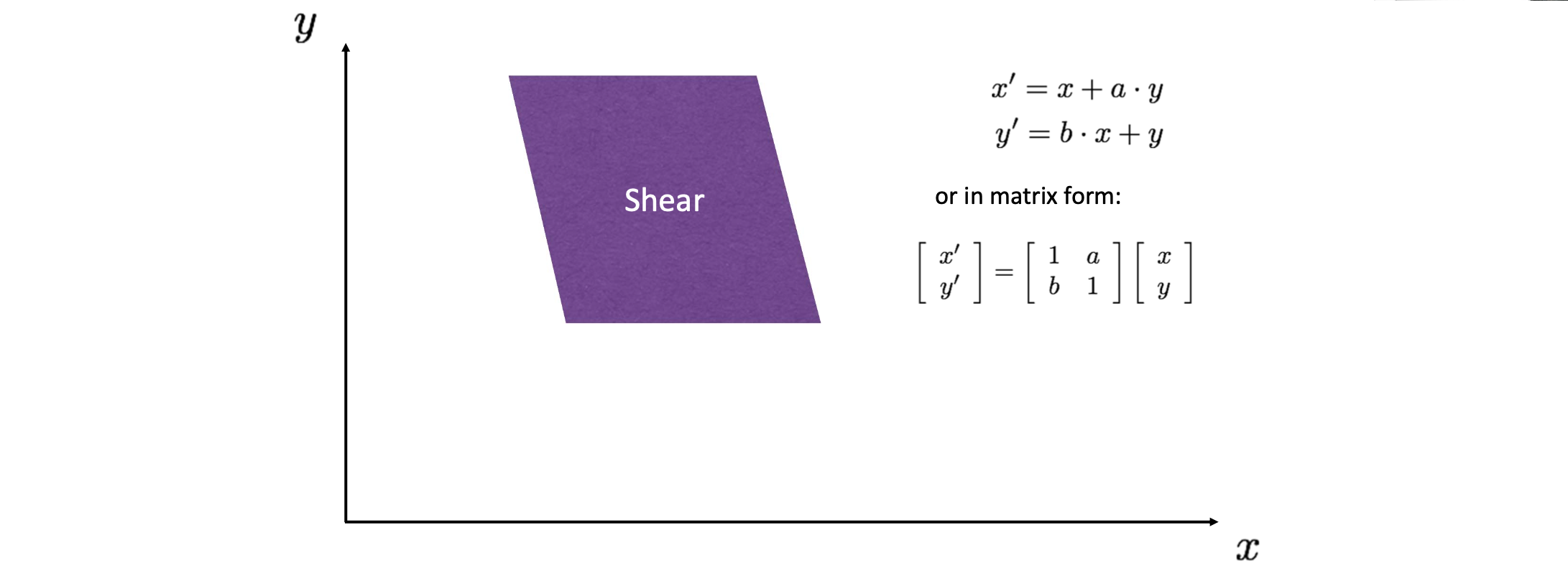
옆으로 민 것 같은 Shearing 형태는 위와 같이 만들 수 있습니다.
그 다음으로 바로 Rotation 입니다. 고등학교 때 배웠듯이 삼각함수를 이용하면 시게 반대 방향으로 만큼 돌렸을 때의 좌표를 알 수 있습니다. 결과는 아래와 같습니다.
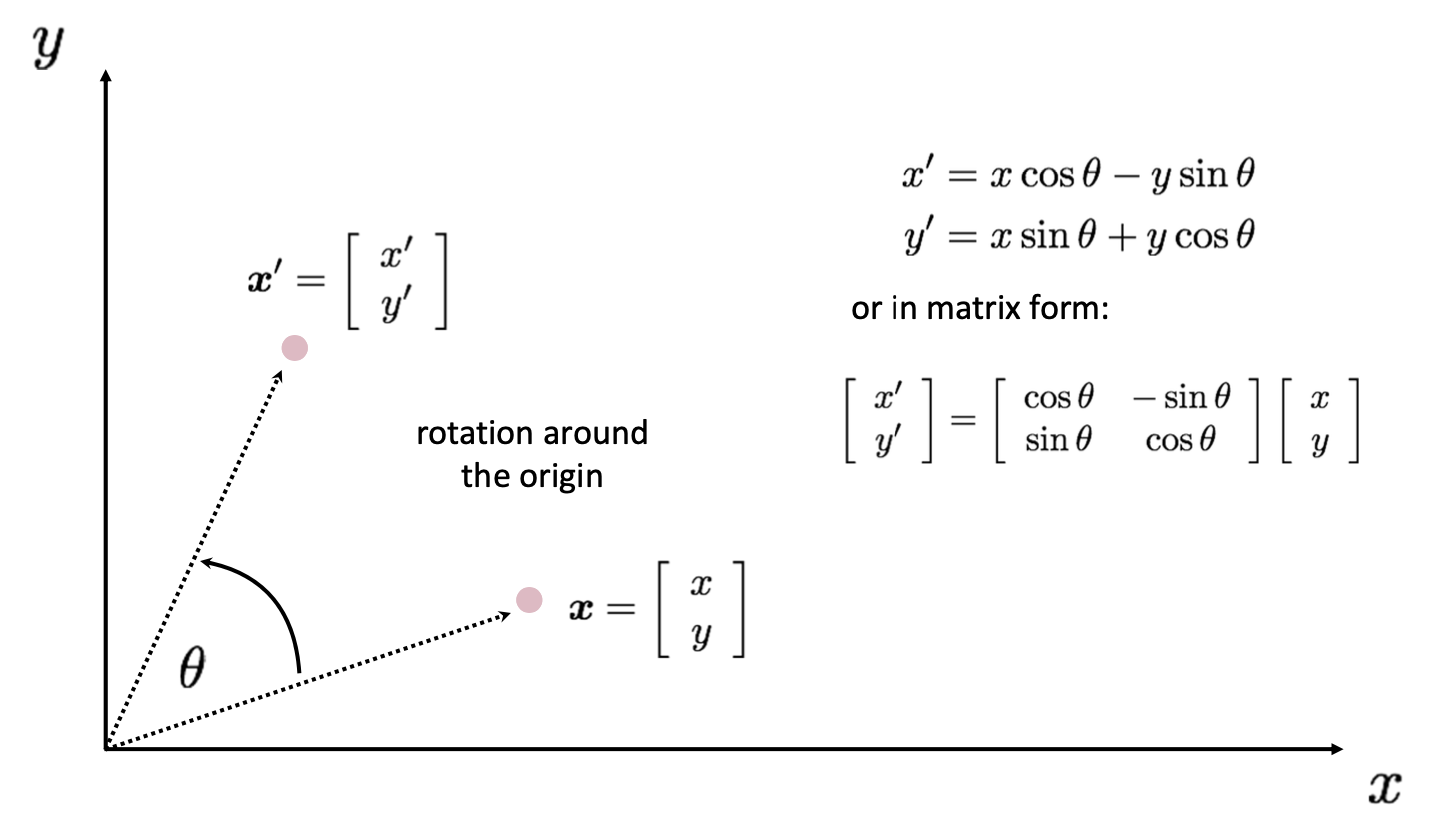
에시를 보면서 자연스럽게 습득하셨겠지만 결국 우리는 를 아래와 같이 matrix 로 표현하고 싶은 겁니다.
( = parameter )
이와 같이 다양한 목적을 위한 은 아래와 같습니다.
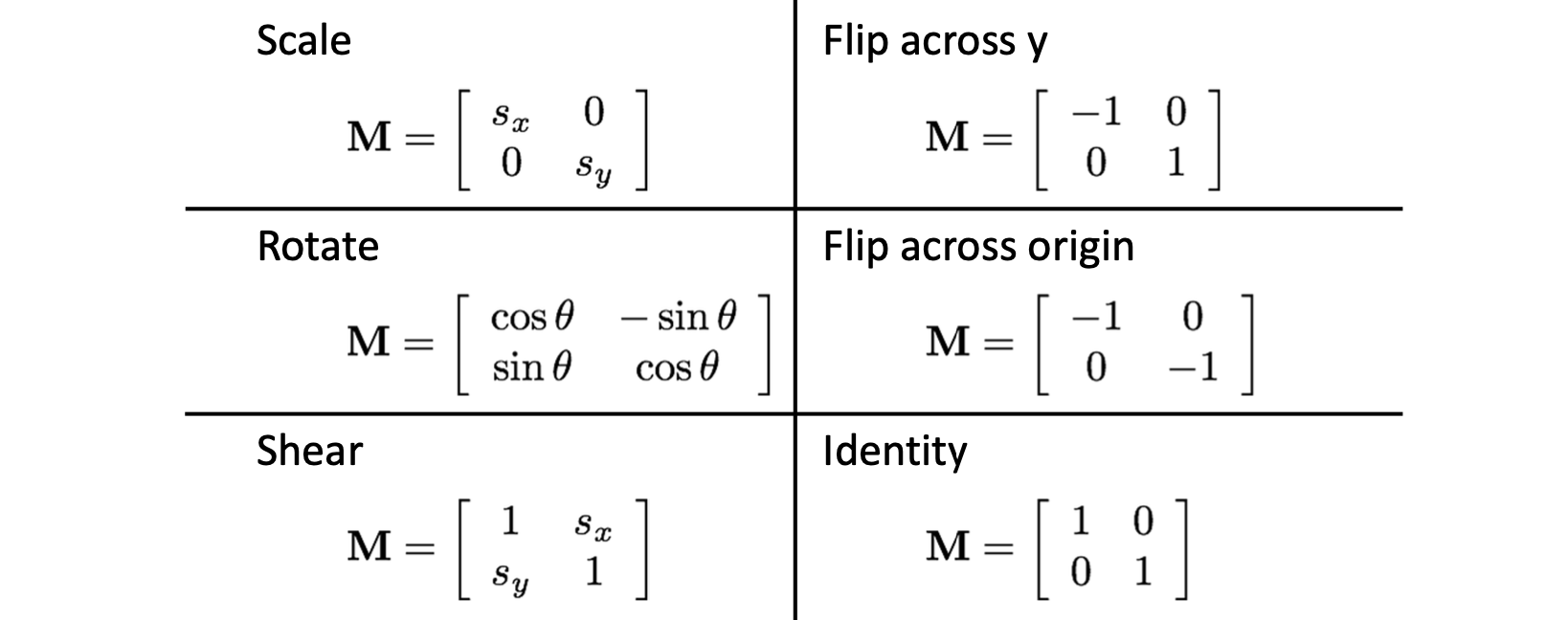
새로 보이는 것은 축을 기준으로 회전, 원점을 기준으로 회전, 그리고 원본 그대로 보존하는 matrix 입니다. 그런데 여기서 관건은 평행이동 2D Translation 입니다. 아래 예시를 보시죠.
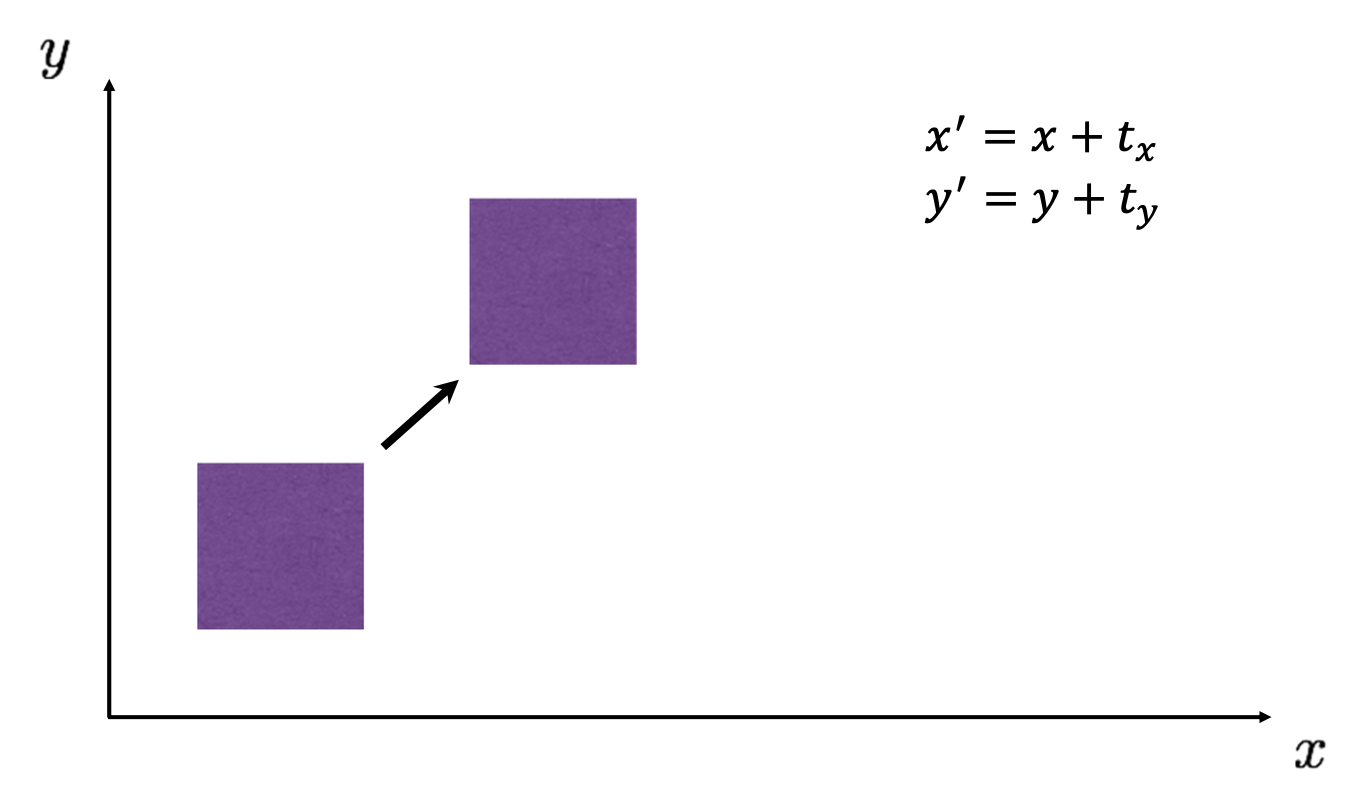
이미지를 축으로 만큼, 축으로 만큼 평행이동 한 것에 대한 식은 위와 같이 쉽게 구할 수 있습니다. 그렇다면 이를 이용해 matrix 을 생각해 보실까요? 떠오르질 않죠? 맞습니다. 와 곱을 해서는 나 값을 도출해낼 수가 없습니다. 이제부터는 이런 Translation 문제까지 어떻게 하면 단일 모델로 해결을 할 수 있을까에 대해 얘기해보도록 하겠습니다.
Projective Geometry Basics
우리가 일반적으로 생각하고 있는 좌표계를 heterogeneous coordinates 라고 하며, 2D 좌표를 아래와 같이 로 표현합니다. 그런데 우리가 알아야 할 homogeneous coordinates 는 이와 같은 2차원 점을 3차원 벡터로 표현하기 위해 가장 아래에 1을 덧붙여 로 표현합니다.
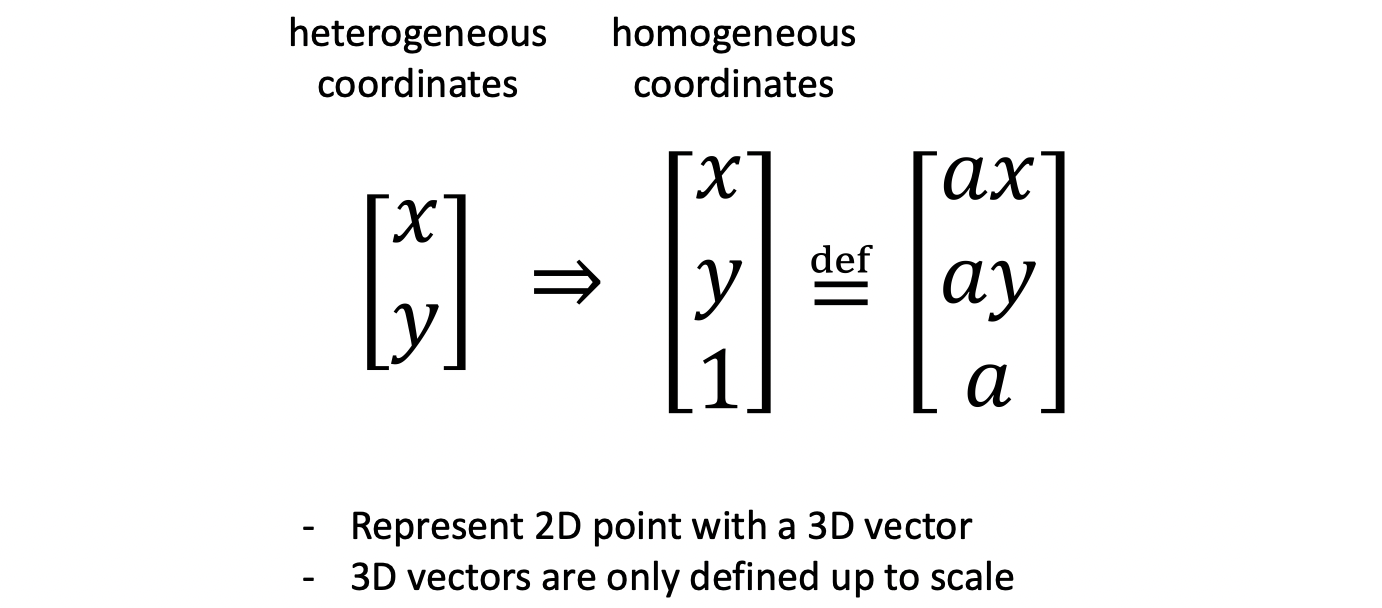
그리고 특이한 점은 이 homogeneous coordinates 는 scale invariance 합니다. 따라서 위 그림과 같이 어떤 벡터와 그것의 상수배를 같다고 보는 겁니다. 다시 말하자면 두 벡터의 마지막 요소를 1로 했을 때 위의 두 값이 같다면 이는 homogeneous coordinates 상에서 같은 벡터(점)이 됩니다.
그렇게 로 확장을 한다면 아래와 같이 로 이전에 matrix로는 하지 못하였던 2D Transformations 를 할 수 있게 됩니다.

homogeneous 를 heterogeneous 로 바꾸고 싶다면 이 되는 것입니다. 그리고 언급하였듯이 homogeneous 에서는 Scale Invariance 의 특성으로 인해 가 성립합니다. 이것이 의미하는 것은 다음과 같습니다.
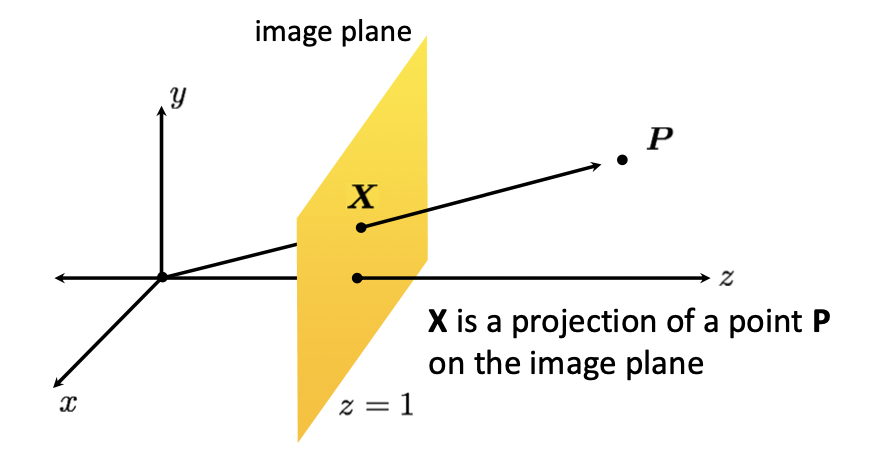
z = 1 인 3차원 상에서의 평면을 image plane 이라 한다면 은 이 평면 위의 한 점입니다. 그리고 일 때, 는 를 원점에 대하여 image plane 으로 Projection 한 결과입니다. 따라서 에서 선 상의 모든 점, 아니 이후의 모든 점들까지 homogenous 상에서는 와 같은 점이라고 얘기할 수 있게 됩니다. 이러한 homogenous coordinates 를 Projective Geometry 라고 표현합니다.
Transformation in Projective Geometry
Projective Geometry 를 써서 Translation 이 가능해졌습니다. 물론 3행과 3열에 을 채워서 이미 구하였던 scaling, rotation, shearing 에 대한 matrix 도 으로 확장시켜 homogenous 상에서 구할 수 있습니다. 아래와 같습니다.
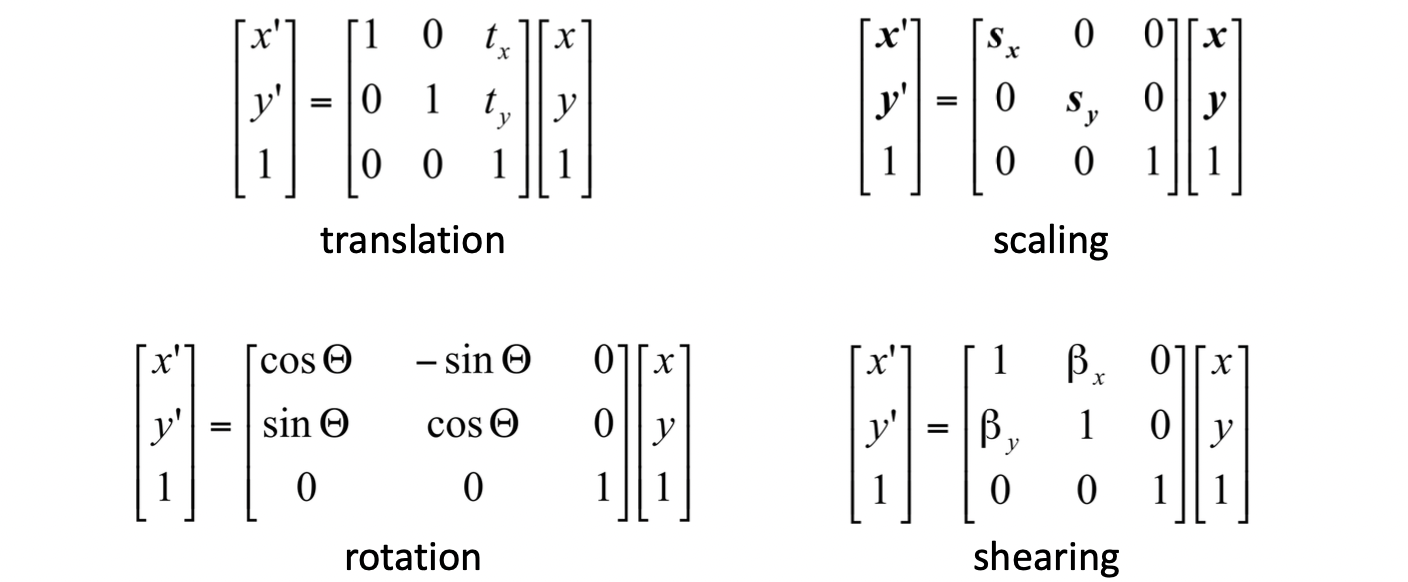
또한 이 matrix 은 여러 trasformation matrix 에 대한 곱으로 표현할 수가 있습니다. 아래의 예시를 봅시다.
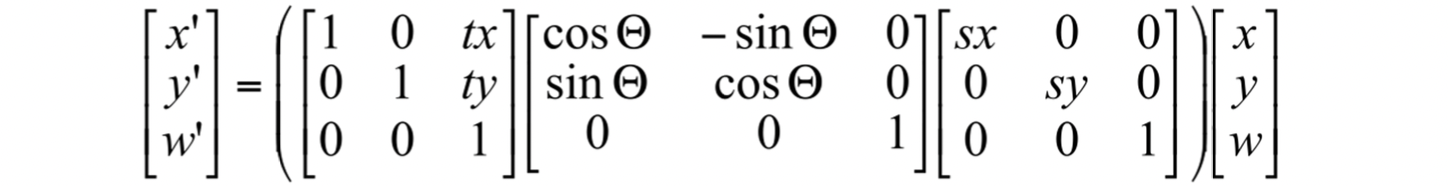
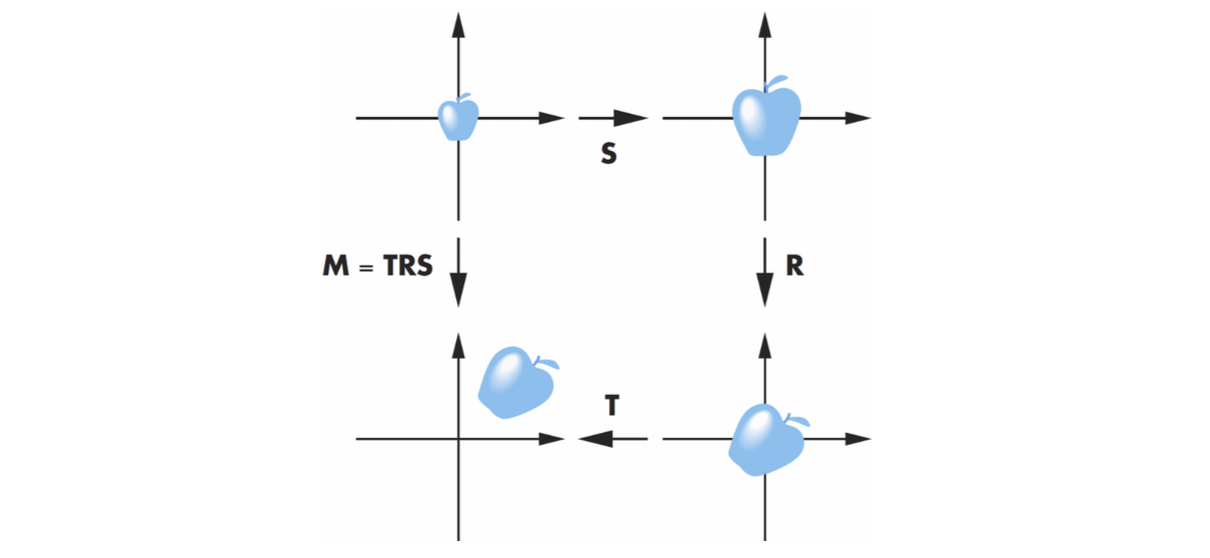
오른쪽부터 scaling, rotation, translation 인데 굳이 scaling 을 구하고 그것을 이용해 rotation을 구하고 그것으로 translation 을 구할 필요 없이 이 세 가지 matrix 를 곱해 미리 하나의 transformation, 즉 matrix 으로 만들 수 있습니다. 이렇게 되면 이 으로 scaling - rotation - translation 이 한 번에 가능해지는 것입니다. 즉 다음과 같은 수식이 성립하는 것이지요.
그리고 이 에시와 같이 scaling, rotation, translation, 즉 다시 표현해 scale, orient, locate 이 다 들어가있는 transformation 을 Instance Transformation 이라고 부릅니다. 하나의 이미지를 통해서 여러 instance 들을 만들 수 있기 때문에 이와 같이 이름이 붙여졌습니다. 실제로 게임 속에서 메모리를 아끼기 위해 하나의 미니언 캐릭터를 가지고 tranformation 해 여러 미니언들을 만들 때 사용하고는 합니다.
Classification of 2D Transformations
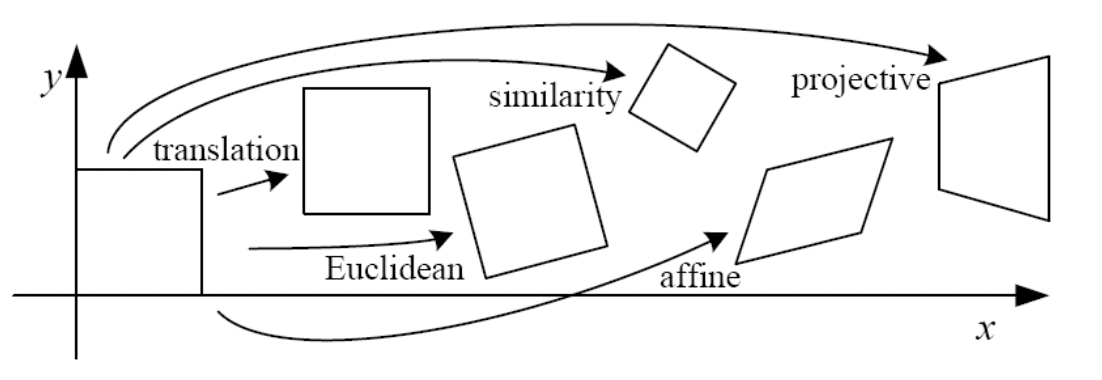
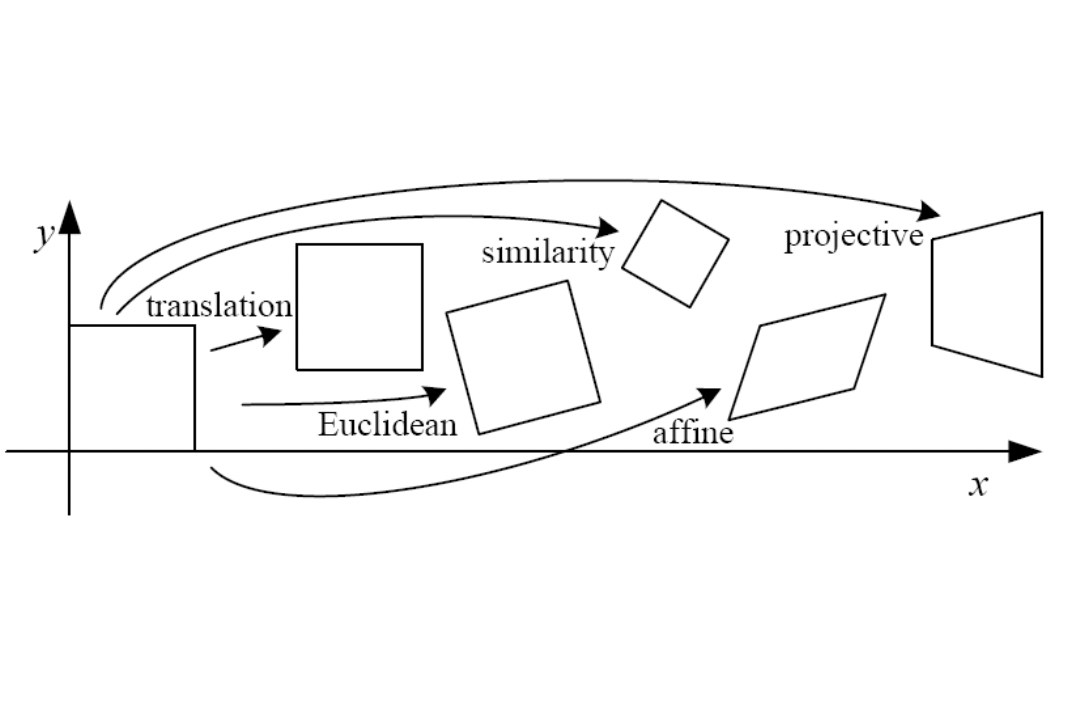
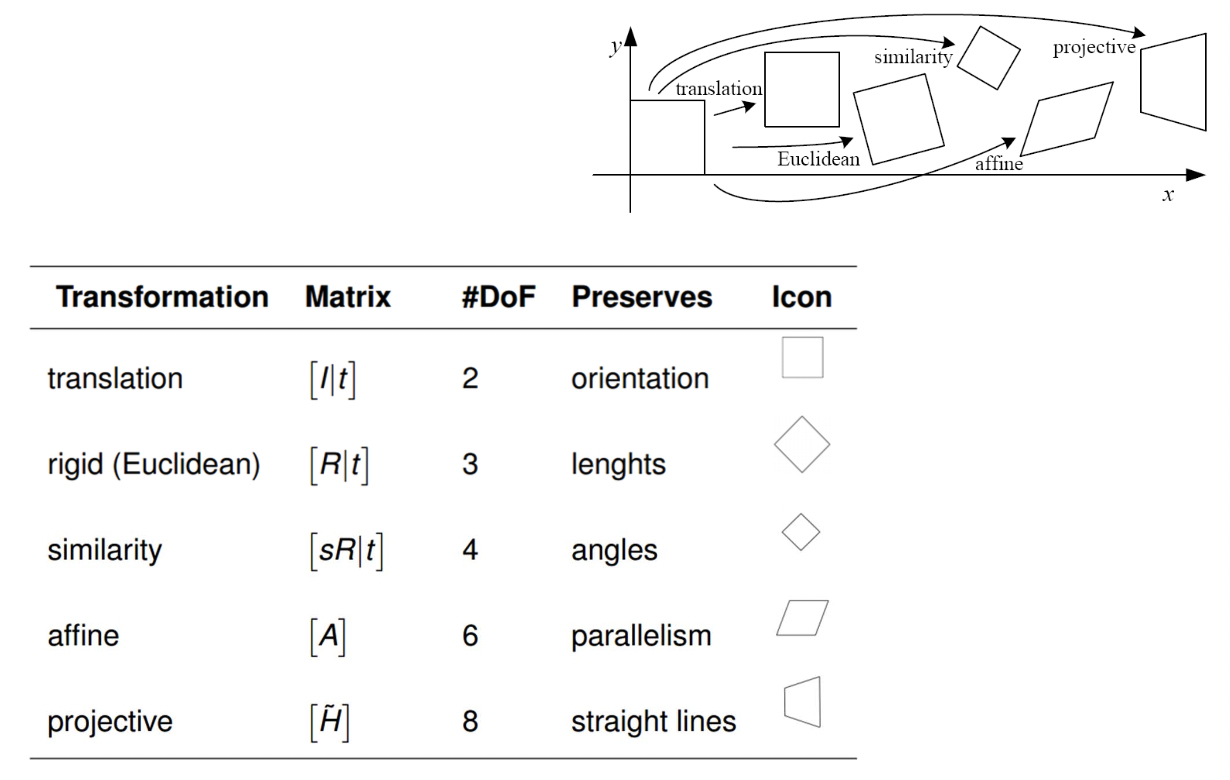
2D Transformations 에는 대표적으로 크게 위와 같은 5개가 있습니다. 이 들을 분류해보죠. 첫 번 째 기준으로는 Degree of Freedom(DOF) 를 해봅시다. 값을 설정할 수 있는 변수, 즉 설정할 수 있는 값들이 얼마나 있는지를 봅시다.
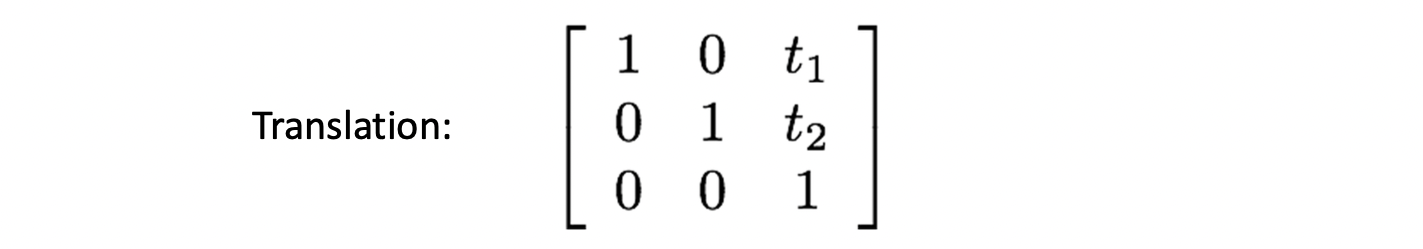
먼저 Translation 입니다. 과 로 DOG 가 2 입니다.
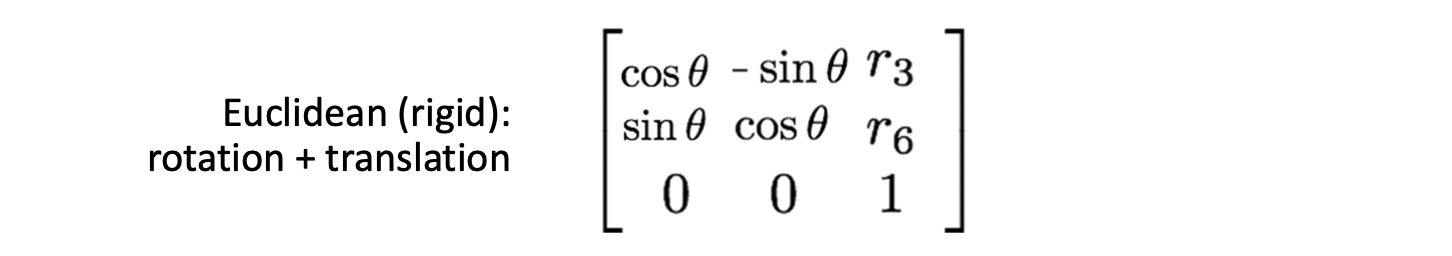
Euclidean 은 Translation 에 Rotation 을 더한 것으로 모양은 바뀌지 않는 특징을 지닙니다. 로 DOG 가 3입니다.
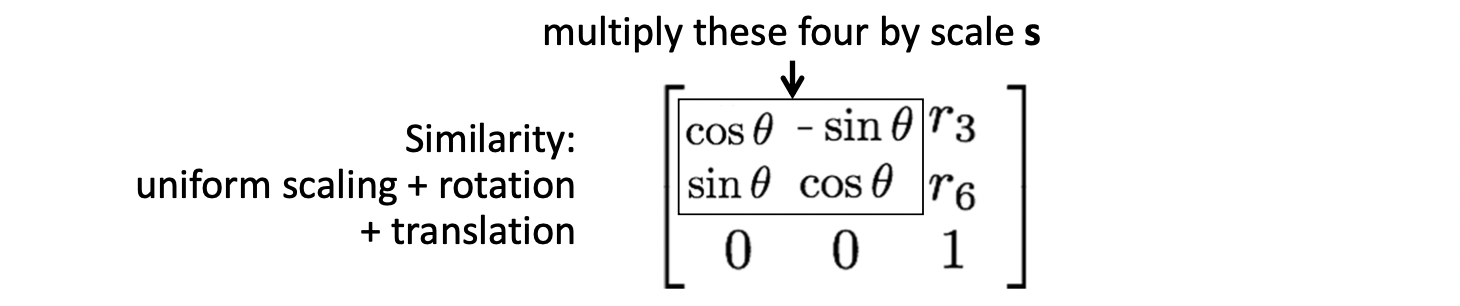
Similarity 는 Euclidean 에 Scaling 을 더한 것입니다. 따라서, 로 DOG 가 4입니다.
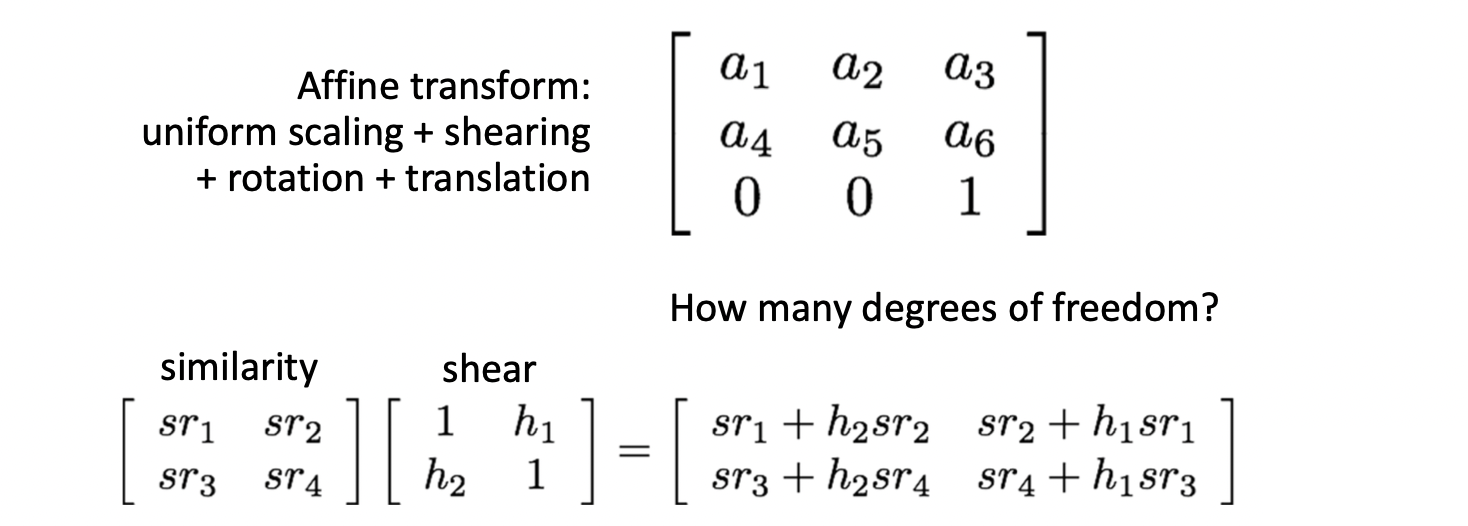
Affine 은 이 Similarity 에 Sheering 까지 더한 것입니다. (위의 그림에서는 ). 따라서 까지 추가되어 DOG 가 6이 되게 됩니다. 이러한 Affine 은 아래와 같은 특징을 지닙니다.
- 원점이 원점으로 매핑되지 않습니다. (translation 때문에)
- 선은 선으로 매핑됩니다.
- 평행한 두 선은 매핑 이후에도 평행합니다.
- 가로 - 세로 비율이 유지됩니다.
- Affine 을 섞어도 Affine 이 됩니다.
마지막으로 Projective 는 이와 같은 Affine 에 projectvie wraps 를 더한 것입니다. Affine 까지는 matrix 의 세 번째 열이 항상 로 항상 상에서의 평면에서 일어나는 일들입니다. 그런데 이 값이 변수가 되서 project 하는 평면도 바뀌는 겁니다. 따라서 위와 같은 모양이 나오는 것입니다. 이러한 Projective 는 다음과 같은 특징을 지닙니다.
- 원점은 원점으로 매핑되지 않습니다.(translation 때문에)
- 선은 선으로 매핑됩니다.
- 평행한 두 선은 매핑 후 평행하지 않을 수 있습니다.
- 가로-세로 비율이 유지되지 않습니다.
- Projective 를 섞어도 Projective 가 됩니다.
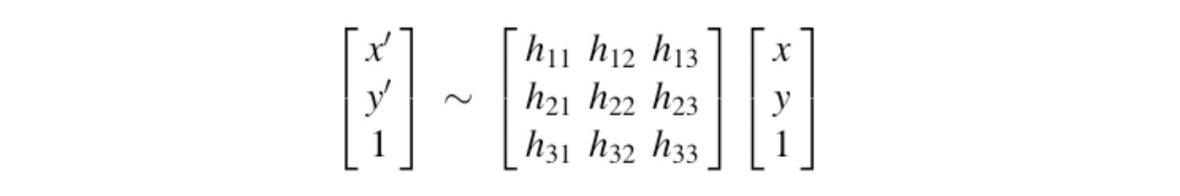
이렇게만 보면 Projective 의 DOG 는 9여야 할 것 같습니다. 하지만 Projective Geometry 의 Scale Invariance 를 생각해보면 matrix 의 모든 요소를 값으로 나누어 3행 3열을 항상 1로 유지해도 무방합니다. 따라서, DOG 는 8이 되게 됩니다.
최종적으로 정리한 결과는 아래와 같습니다.
Determining Unknown 2D Transformations
이제 본론으로 들어가 매칭 관계를 알고 있을 때 어떻게 하면 Transformation 을 알아낼 수 있는지에 대해 이야기 해봅시다.
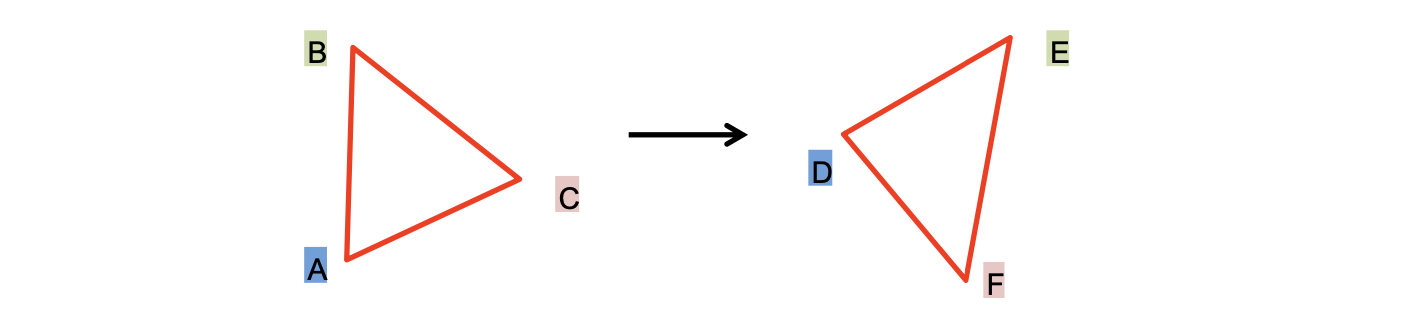
예시는 위 그림과 같습니다. 우리가 두 이미지에 대해 A - D, C - E, B - E 로 매핑된다는 것을 알 때 Transformation Function 을 구하고 싶은 겁니다. 먼저, Model 을 Affine Transform 으로 설정해봅시다. 즉, 식을 통해서 포인트 하나에 아래와 같은 두 가지 식을 유도할 수 있습니다.
우리가 구하고 싶은 parameter 의 개수, 즉 DOG 는 6개인데 점 세개를 통해서 총 6개의 식을 유도할 수 있기 때문에 를 알아낼 수 있는 겁니다. 따라서, 이렇게 하면 Affine Model 로 딱 들어맞는 Transformation Function 을 찾을 수 있게 되는 겁니다.
그런데 우리가 실제로 이를 수행할 때는 각기 다른, 보통 3개가 넘는 매칭 정보들이 존재합니다. 그래서 Affine Model 만 하더라도 이 모든 매칭 정보들에 딱 들어맞는 parameter 는 찾는 것이 불가능합니다. 그래서 우리는 최대한으로 들어맞게 하자는 겁니다. 매칭 정보들에 대하여 Transformation 한 값과의 차이가 최소가 되게끔 하는 것이 목표이며 이것은 Least Squares Error 라고 다음과 같이 정의합니다.
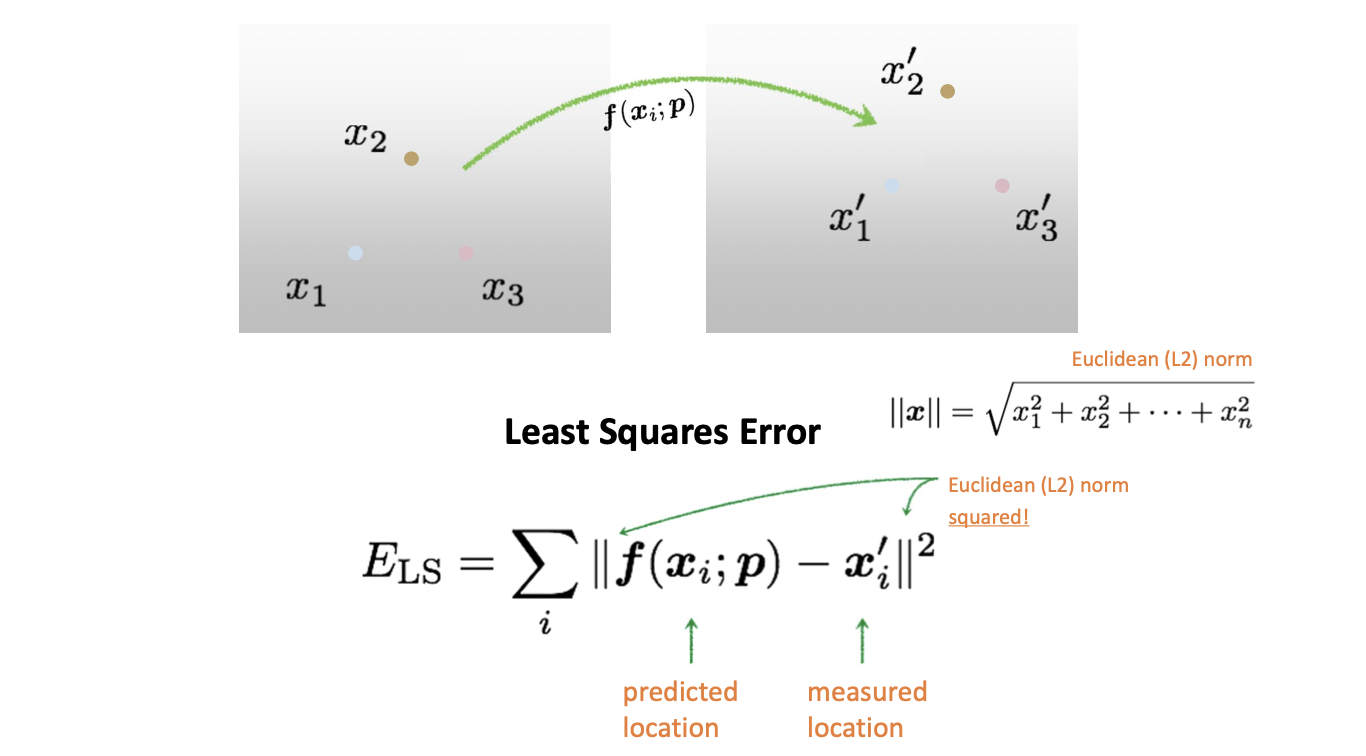
차의 절댓값들을 모은 후 더해서 이를 최소로 하는 paramter p 를 구하는 것이 목표입니다. 차가 클수록 더 크게 반영해주기 위해 제곱을 합니다.
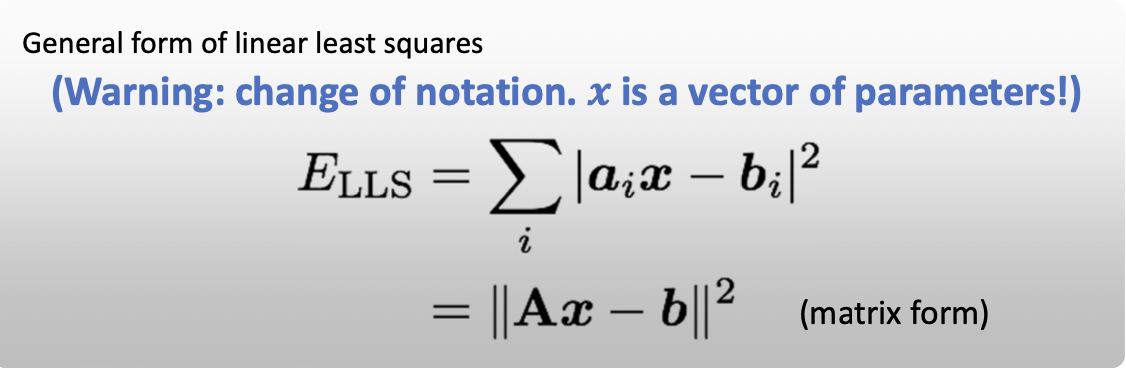
선형상에서 일반화한 식 Linear Least Squares 는 위와 같습니다. Transformation 이전의 값들 에 parameter vector 인 로 계산한 결과와 Transformation 이후의 값들 의 차에 절댓값을 취해 제곱합니다. 이 들을 쌓아서 를 만들 수 있습니다. Affine Model 에서의 예시를 들면 아래와 같습니다.
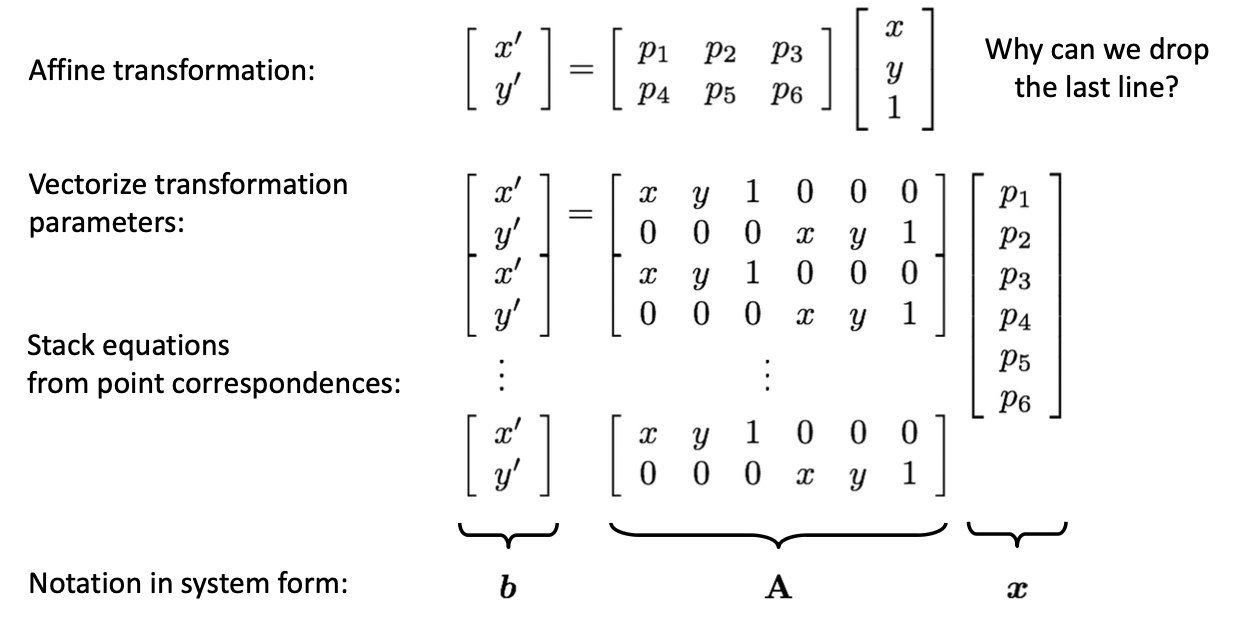
먼저 에서 3열은 항상 이기 때문에 parameter 만 남겨도 무방합니다. 그리고 위의 식에서 확인할 수 있다시피 가 최소가 되기 위한 경우는 인 경우입니다. 따라서 매핑 정보들에 줄 지어서 에 부합하는 위와 같은 형태로 표현할 수 있습니다.
그 다음 한 번 Linear Least Squares 를 풀어봅시다.
그런데 여기서 값이 스칼라 값이니 모든 항, 즉 또한 스칼라 값이 되어야 한다. 스칼라 값의 Transpose 는 같기 때문에 이를 이므로 최종적으로 식은 아래와 같이 나온다.
최솟값이 나오기 위해서는 미분한 값이 0 이여야 한다.
이 식을 풀면 결과적으로 최소가 되기 위한 는 다음과 같다.
