CPSC 223 - Sort

Heap Sort

Bottom-up heapification is used in the Heapsort algorithm, which first does bottom-up heapification in O(n) time and then repeatedly calls DELETE-MAX to extract the largest remaining element. This is no faster than the O(nlogn) cost of mergesort or quicksort in typical use, but requires very little auxiliary보조 storage since we can maintain the heap in the bottom part of the same array whose top part stores the max elements extracted so far.

Mergesort

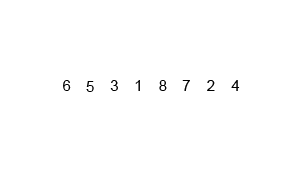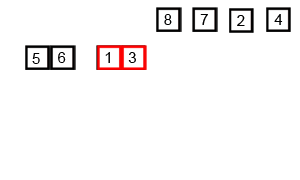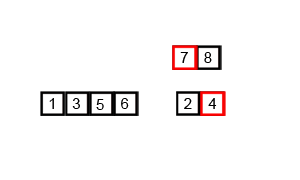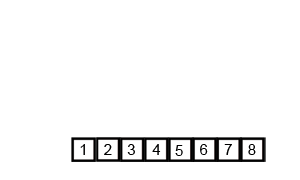
A recursive sorting algorithm & a classic divide and conquer sorting algorithm.
It splits an array into two pieces, sorts each piece (recursively!), then merges the results back together.

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

// merge sorted arrays a1 and a2, putting result in out
void merge(int n1, const int a1[], int n2, const int a2[], int out[])
{
    int i1;
    int i2;
    int iout;

    i1 = i2 = iout = 0;

    while(i1 < n1 || i2 < n2) {
        if(i2 >= n2 || (i1 < n1) && (a1[i1] > a2[i2])) {
            // a1[i1] exists and is smaller
            out[iout++] = a1[i1++];
        }
        else {
            // a1[i1] doesn't exist, or is bigger than a2[i2]
            out[iout++] = a2[i2++];
        }
    }
}

// sort a, putting result in out
// we call this mergeSort to avoid conflict with mergesort in libc
void mergeSort(int n, const int a[], int out[])
{
    int *a1;
    int *a2;

    if(n < 2) {
        // 0 or 1 elements is already sorted
        memcpy(out, a, sizeof(int) *n );
    }
    else {
        // if n = 6, a1 = 3, a2 = 3
        // if n = 5, a1 = 2, a2 = 3
        a1 = malloc(sizeof(int)* (n/2));
        a2 = malloc(sizeof(int)* (n - n/2));

        // split 
        mergeSort(n/2, a, a1);
        mergeSort(n - n/2, a + n/2, a2);

        // for(int i = 0 ; i < n/2 ; i++) {
        //     printf("%d ", a1[i]);
        // }
        // printf("\n");
        // for(int i = 0 ; i < n/2 ; i++) {
        //     printf("%d ", a2[i]);
        // }
        // printf("\n");
        // merge results
        merge(n/2, a1, n - n/2, a2, out);

        free(a1);
        free(a2);
    }
}

#define N 20

int main(int argc, char **argv)
{
    int a[N] = {19,1,18,4,16,17,2,3,5,12,13,11,9,10,8,6,7,14,4,15};
    int b[N];
    int i;

    // for(i = 0 ; i < N ; i++) {
    //     a[i] = N-i-1;
    // }

    for(i = 0 ; i < N ; i++) {
        printf("%d ", a[i]);
    }
    putchar('\n');

    mergeSort(N, a, b);

    for(i = 0 ; i < N ; i++) {
        printf("%d ", b[i]);
    }
    putchar('\n');

    return 0;
}

Quicksort

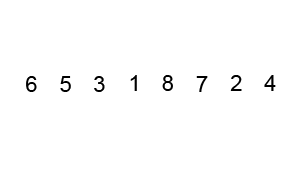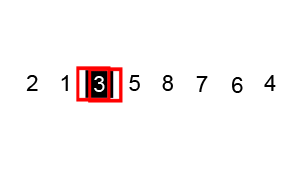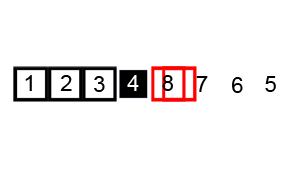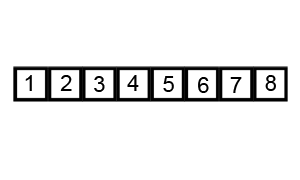
Quickselect, or Hoare's FIND (Hoare, C. A. R. Algorithm 65: FIND, CACM 4(7):321–322, July 1961), is an algorithm for quickly finding the k-th largest element in an unsorted array of n elements. It runs O(n) time on average, which is the best one can hope for (we have to look at every element of the array to be sure we didn't miss a small one that changes our answer) and better than the O(nlogn) time we get if we sort the array first using a comparison-based sorting algorithm.

The idea is to pick a random pivot and divide the input into two piles, each of which is likely to be roughly a constant fraction of the size of the original input. It takes O(n) time to split the input up, and in the recursive calls this gives a geometric series. We can even do the splitting up in place if we are willing to reorder the elements of our original array.

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>

// Reorder an array to Put elements <= pivot
// Before elements > pivot
// Returns number of elements <= pivot
static int splitByPivot(int n, int *a, int pivot) {
    int lo;
    int hi;
    int temp;

    assert(n >= 0);

    lo = 0;
    hi = n-1;

    while(lo <= hi) {
        if(a[lo] <= pivot) {
            lo++;
        }
        else {
            temp = a[hi];
            a[hi--] = a[lo];
            a[lo] = temp;
        }
    }

    return lo;
}

int quickSelectDestructive(int k, int n, int *a) {
    int pivot;
    int lo;

    assert(0 <= k);
    assert(k < n);

    if (n == 1) {
        return a[0];
    }

    // we will tolerate non-uniformity
    pivot = a[rand() % n];

    lo = splitByPivot(n, a, pivot);

    // lo is now number of values <= pivot
    if(k < lo) {
        return quickSelectDestructive(k, lo, a);
    }
    else {
        return quickSelectDestructive(k - lo, n - lo, a + lo);
    }
}

void quickSort(int n, int *a) {
    int pivot;
    int lo;

    if (n <= 1) {
        return;
    }

    // we will tolerate non-uniformity
    pivot = a[rand() % n];
    lo = splitByPivot(n, a, pivot);

    quickSort(lo, a);
    quickSort(n - lo, a + lo);
}

void shuffle(int n, int *a) {
    int i;
    int r;
    int temp;

    for(i = n - 1; i > 0 ; i--) {
        r = rand() % i;
        temp = a[r];
        a[r] = a[i];
        a[i] = temp;
    }
}

#define N 1024

int main(int argc, char **argv)
{
    int a[N];
    int i;

    // used fixed value for debugging
    srand(0);

    for(i = 0 ; i < N ; i++) {
        a[i] = i;
    }

    shuffle(N, a);

    for (i = 0 ; i < N ; i++) {
        assert(quickSelectDestructive(i, N, a) == i);
    }

    shuffle(N, a);

    quickSort(N, a);

    for (i = 0 ; i < N ; i++) {
        assert(a[i] == i);
    }

    return 0;
}

Ref)
https://commons.wikimedia.org/wiki/File:Heapsort-example.gif
https://commons.wikimedia.org/wiki/File:Quicksort-example.gif
https://commons.wikimedia.org/wiki/File:Merge-sort-example-300px.gif