바이너리 인덱스 트리(펜윅트리)

지난 글에 이어서 구간합을 구하는데 자주 활용되는 바이너리 인덱스 트리에 대해 알아보겠다. 시간복잡도를 O(logN)까지 줄일 수 있는 효자 알고리즘이다.

필자는 바이너리 인덱스 트리를 Prefix Sum의 업데이트 버전이라고 생각하는 편인데, Prefix Sum으로 구간합을 구할 때 발생하는 단점을 보완해주기 때문이다.

Prefix Sum을 활용하여 누적합 배열을 만든다면 특정 구간의 합을 단순히 두 위치의 값을 빼주어 상수 시간(물론 배열을 만드는데 O(N)소요) 안에 쉽게 구할 수 있다. 그러나 만약 배열의 값이 자주 바뀐다면 어떻게 될까?

예를 들어 원래 배열의 k번째 값이 바뀐다면, 누적합 배열의 k번째와 그 이후의 값들을 모두 바꿔주어야 할 것이다. 여기서 k의 값 자체가 0과 가까운 수라면, 누적합의 배열의 값들을 거의 다 변경해야한다.

따라서 데이터의 양이 많으면서 또 자주 수정된다면 Prefix Sum을 활용하는 것은 효율적이지 않다. 이를 해결하기 위해 등장한 알고리즘이 펜윅트리이다.

펜윅 트리의 구조

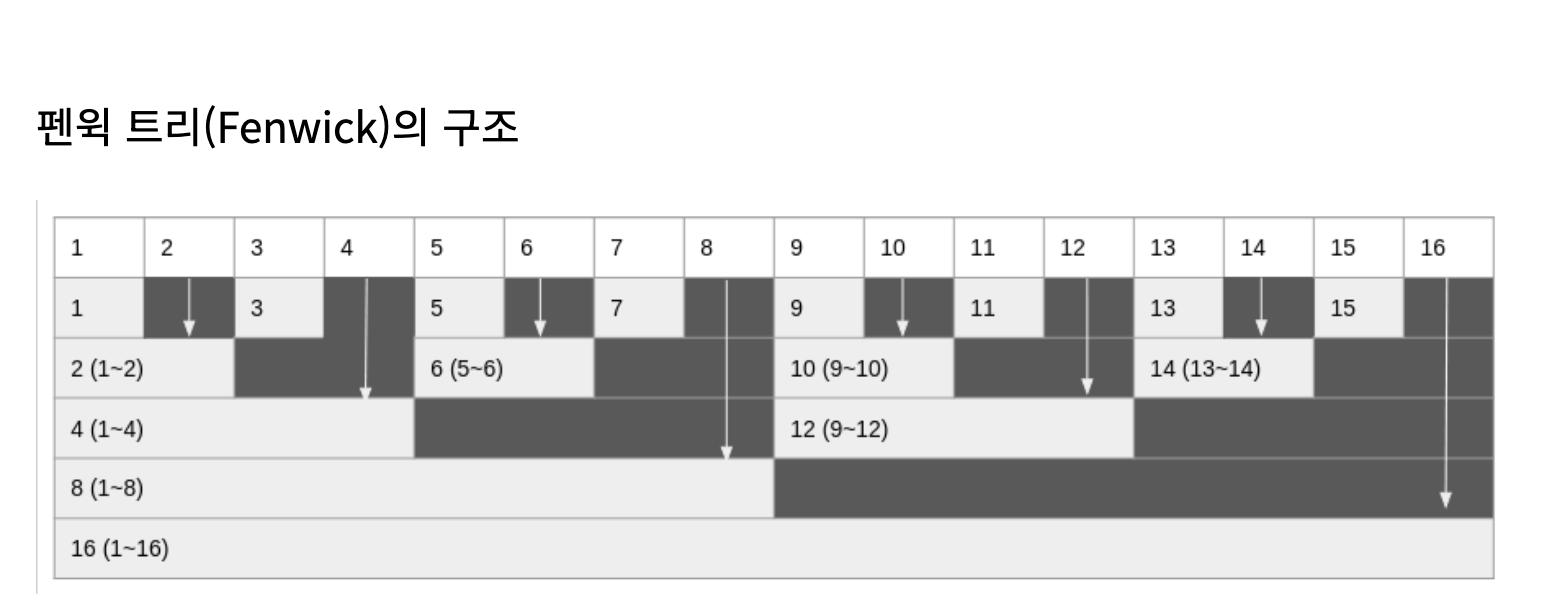
위 그림에서 각 배열의 값은 특정 구간의 합을 의미하는데 예를 들어 3번째 값의 경우 3을, 6번째 값의 경우 5부터 6까지의 합을, 마지막으로 12번째 값의 경우 9부터 12까지의 합을 나타낸다.

즉 우리는 펜윅 트리 배열을 보고 특정번째 값이 특정 구간의 합을 알 수 있으며 이들의 조합을 통해 구간합을 구할 수 있다.

그렇다면 펜윅트리의 k번째 값은 어떤 규칙에 의해서 어디까지의 구간합을 갖고 있는것일까?

이진법 표현을 활용한 펜윅트리의 규칙

펜윅트리는 배열 인덱스의 이진법 표현을 활용한 자료구조이다.
먼저 각 배열의 인덱스 값에 대하여 이진수로 표현했을 때 0이 아닌 마지막 비트를 찾는다. 예를 들어 인덱스 12의 경우 1100 (2) 이므로 0이 아닌 마지막 비트는 100 (2)=4(10) 이다. 결국 인덱스 12 번째 값은 자기 자신을 포함해 앞으로 4번째 값까지의 합을 갖고 있다고 해석할 수 있다. 아래 예시들을 통해 자세히 살펴보자.

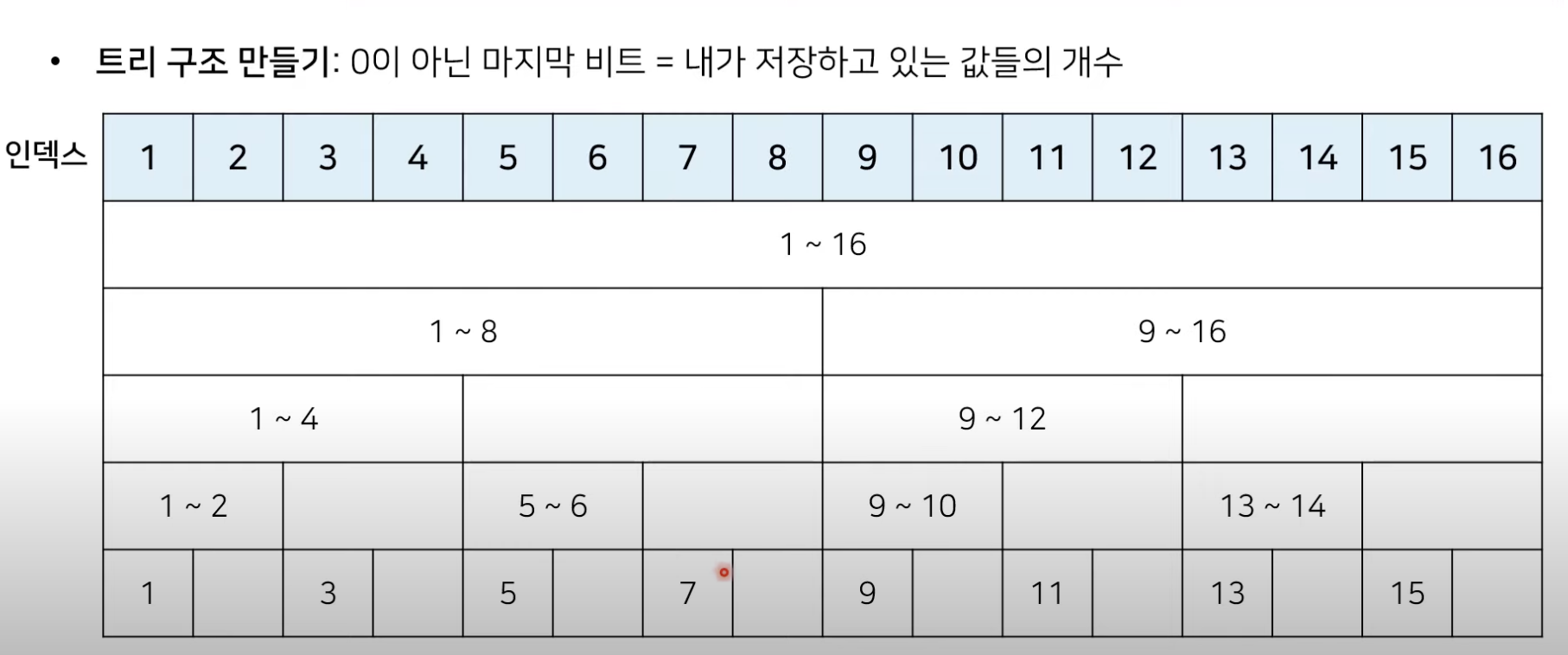
• k = 6 일 때
  • 6은 2진법으로 0110(2)이다. 이때 0이 아닌 마지막 비트는 0010(2) = 2이다.
  • 즉, 자기자신을 포함해 앞으로 2번째 값까지의 합인 5~6의 합을 갖고 있다고 해석할 수 있다.
• k = 3 일 때
  • 3은 2진법으로 0011(2)이다. 이때 0이 아닌 마지막 비트는 0010(2) = 1이다.
  • 즉, 자기자신 포함해 앞으로 1번째 값까지의 합인 3을 갖고 있다고 해석할 수 있다.
• k = 8 일 때
  • 8은 2진법으로 1000(2)이다. 이때 0이 아닌 마지막 비트는 LSBIT(k) = 1000(2) = 8이다.
  • 즉, 자기자신 포함해 앞으로 8번째 값까지의 합인 0~8의 합을 갖고 있다고 해석할 수 있다.

참고로 각 인덱스 값 0이 아닌 마지막 비트를 찾기 위해선 K&-K를 계산하면 된다.

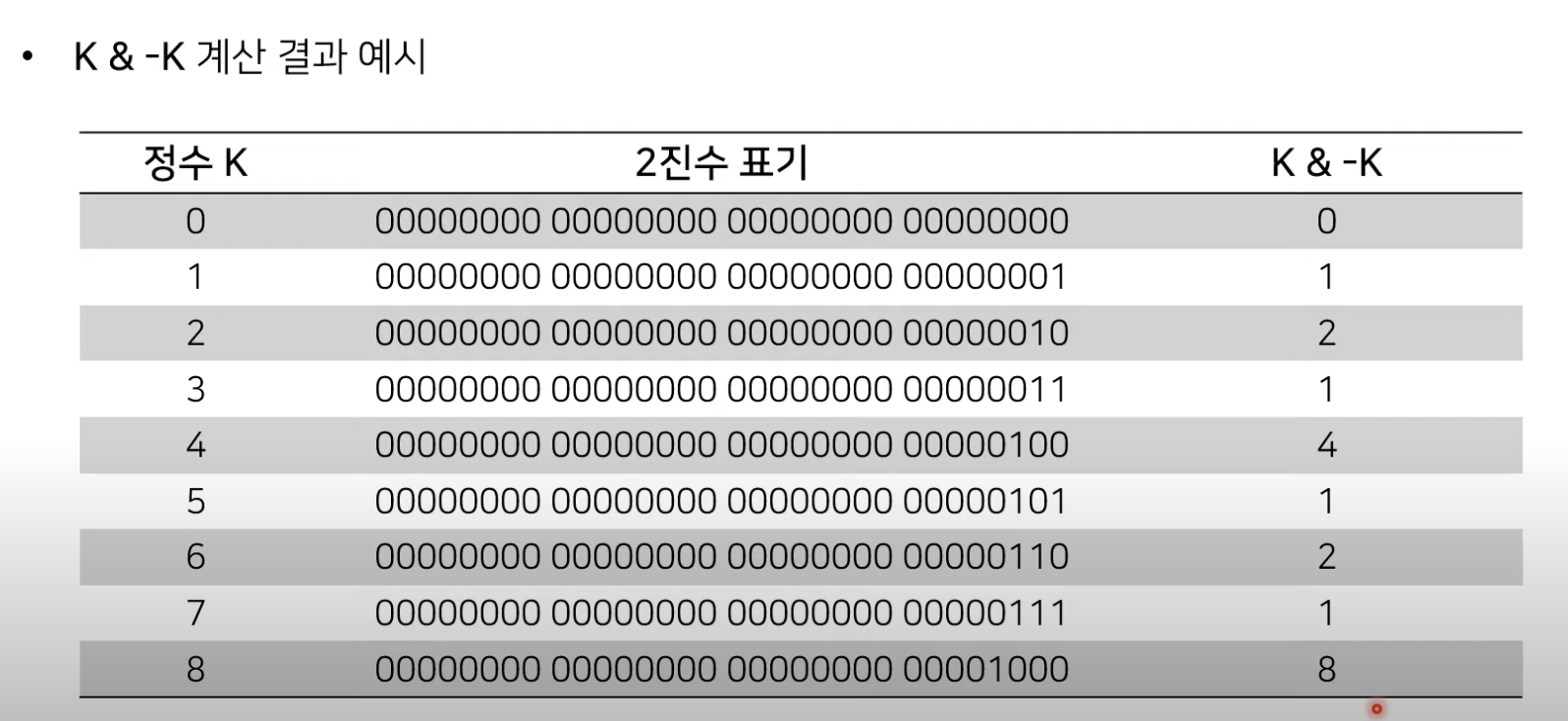
펜윅트리를 활용해 데이터를 업데이트 해보자

만약 원본 배열의 k번째 값이 변경되었다면 펜윅트리에서는 원본 배열의 k번째 값을 포함하고 있는 모든 값을 수정해주어야 한다. 예를 들어 원본 배열의 3번째 값이 3으로 변경되었다고 가정해보자. 그렇다면 아래 그림에서 3,4,8,16 번째 값들을 업데이트 해주어야 할 것이다. (해당 인덱스들의 값들이 3번째 값을 포함하고 있으므로)

여기서 이제 펜윅트리에서 k번째 값을 포함하고 있는 인덱스들을 어떻게 접근(순회)하는 지 궁금할 것이다. 🤔 사실 방법은 간단한데, k에 k의 0이 아닌 마지막 비트의 값를 계속 더해나가면 된다. k=3인 경우에 대해서 자세히 살펴보자.

• k = 3 에서 시작
  • 바뀐 값을 arr[k]에 더해준다
    • 정확히는 원래 값과 갱신되는 값의 차이(diff)만큼을 더해준다
  • 3 + 0이 아닌 마지막 비트 1 = 4 이므로 k를 4로 갱신한다
• k = 4 으로 갱신되었다.
  • 바뀐 값을 arr[k]에 더해준다
  • 4 + 0이 아닌 마지막 비트 4 = 8 이므로 k를 8로 갱신한다
• k = 8 으로 갱신되었다.
  • 바뀐 값을 arr[k]에 더해준다
  • 8 + 0이 아닌 마지막 비트 8 = 16 이므로 k를 16으로 갱신한다
• k>16인 인덱스는 없으므로 인덱스 순회(접근)를 종료한다

펜윅트리를 활용해 구간 합을 구해보자

우리는 위 설명을 통해 펜윅트리는 특정 구간의 합을 저장하고 있음을 잘 알고 있다. 이를 활용해 실제 구간 합을 구해보자

만약 인덱스 4부터 7까지의 구간합을 구해야한다면 Prefix Sum과 마찬가지로 arr[7]에서 arr[4]를 빼주는 행위를 할 것이다. 이를 위해 arr[7]과 arr[4] 즉, 인덱스 7까지의 누적합과 인덱스 4까지의 누적합을 먼저 펜윅트리에서 구해야한다.

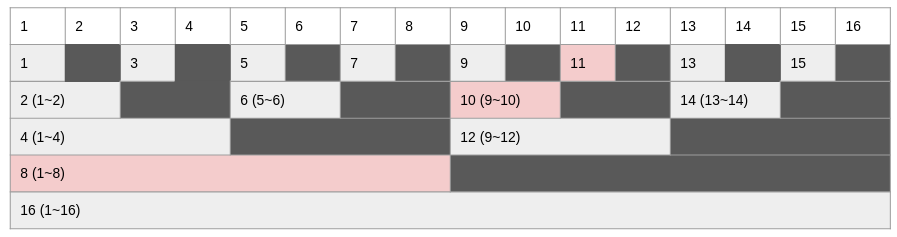
만약 인덱스 11까지의 누적합을 구하려면 위 사진과 같이 빨간 부분의 값들을 뽑아내면 된다. 즉, 11의 경우 인덱스 11, 10, 8에 접근해 이들을 모두 더해주면 된다.

각 인덱스에 접근(순회)하는 방식은 데이터를 업데이트할 때와 마찬가지도 동일하게 동작하는데, 그 때는 k의 값을 0이 아닌 마지막비트를 통해 더해주었다면 여기서는 빼주기만 하면된다.

• k = 11 에서 시작
  • arr[k]를 sum 변수에 더해준다
  • 11 - 0이 아닌 마지막 비트 1 = 10 이므로 k를 10으로 갱신한다
• k = 10 으로 갱신되었다.
  • arr[k]를 sum 변수에 더해준다
  • 10 - 0이 아닌 마지막 비트 2 = 8 이므로 k를 8로 갱신한다
• k = 8 으로 갱신되었다.
  • arr[k]를 sum 변수에 더해준다
  • 8 - 0이 아닌 마지막 비트 8 = 0 이므로 k를 0으로 갱신한다
• k가 0이 되었으므로 인덱스 순회(접근)를 종료한다

구현 코드

import sys

input = sys.stdin.readline

n, m, k = map(int, input().split())

arr = [0] * (n + 1)  # 데이터 업데이트 할 때 원본 배열 과의 diff를 구할 때만 사용됨
tree = [0] * (n + 1)


def prefix_sum(i):
    result = 0
    while i > 0:
        result += tree[i]
        i -= i & -i
    return result


def update(i, diff):
    while i < n + 1:
        tree[i] += diff
        i += i & -i


def interval_sum(start, end):
    return prefix_sum(end) - prefix_sum(start - 1)  # -1 유의


for i in range(1, n + 1):
    x = int(input())
    arr[i] = x
    update(i, x)  # tree 배열 초기 업데이트

for i in range(m + k):
    a, b, c = map(int, input().split())
    if a == 1:  # 업데이트인 경우
        update(b, c - arr[b])
        arr[b] = c
    else:
        print(interval_sum(b, c))

Reference

• https://tempdev.tistory.com/20
• https://everenew.tistory.com/82 (플레급 문제가 많다. 트리 관련 문제를 공부 중이라면 한 번 도전해보길! )