☘️26.제일 작은 수 제거하기
문제 설명
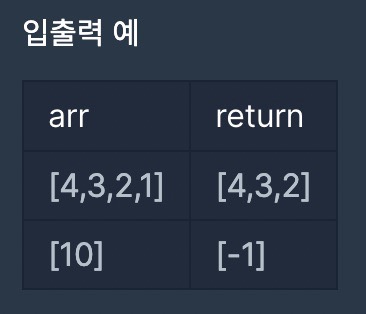
정수를 저장한 배열, arr 에서 가장 작은 수를 제거한 배열을 리턴하는 함수, solution을 완성해주세요. 단, 리턴하려는 배열이 빈 배열인 경우엔 배열에 -1을 채워 리턴하세요. 예를들어 arr이 [4,3,2,1]인 경우는 [4,3,2]를 리턴 하고, [10]면 [-1]을 리턴 합니다.
제한 사항
- arr은 길이 1 이상인 배열입니다.
- 인덱스 i, j에 대해 i ≠ j이면 arr[i] ≠ arr[j] 입니다.
예시
☀️내 코드
class Solution {
public int[] solution(int[] arr) {
int[] answer = new int[arr.length - 1];
int minNum = Integer.MAX_VALUE;
int minIdx = 0;
for(int i = 0; i < arr.length; i++) {
if (minNum >= arr[i]) {
minNum = arr[i];
minIdx = i;
}
}
for (int i = 0; i < minIdx; i++) {
answer[i] = arr[i];
}
for (int i = minIdx + 1; i < arr.length; i++) {
answer[i - 1] = arr[i];
}
if (arr.length == 1) {
answer = new int[1];
answer[0] = -1;
}
return answer;
}
}📌다른 사람 코드
stream을 쓰면 가독성은 좋지만 속도는 정말정말 느린.....
import java.util.Arrays;
import java.util.stream.Stream;
import java.util.List;
import java.util.ArrayList;
class Solution {
public int[] solution(int[] arr) {
if (arr.length <= 1) {
return new int[]{- 1};
}
int min = Arrays.stream(arr).min().getAsInt();
return Arrays.stream(arr).filter(i -> i != min).toArray();
}
}☘️27.콜라츠 추측
문제 설명
1937년 Collatz란 사람에 의해 제기된 이 추측은, 주어진 수가 1이 될 때까지 다음 작업을 반복하면, 모든 수를 1로 만들 수 있다는 추측입니다. 작업은 다음과 같습니다.
1-1. 입력된 수가 짝수라면 2로 나눕니다.
1-2. 입력된 수가 홀수라면 3을 곱하고 1을 더합니다.
2. 결과로 나온 수에 같은 작업을 1이 될 때까지 반복합니다.
예를 들어, 주어진 수가 6이라면 6 → 3 → 10 → 5 → 16 → 8 → 4 → 2 → 1 이 되어 총 8번 만에 1이 됩니다. 위 작업을 몇 번이나 반복해야 하는지 반환하는 함수, solution을 완성해 주세요. 단, 주어진 수가 1인 경우에는 0을, 작업을 500번 반복할 때까지 1이 되지 않는다면 –1을 반환해 주세요.
제한 사항
입력된 수, num은 1 이상 8,000,000 미만인 정수입니다.
예시

☀️내 코드
class Solution {
public int solution(int num) {
int answer = 0;
long x = (long) num;
if (num == 1) {
return 0;
}
while (x != 1) {
if (x % 2 == 0) {
x /= 2;
} else {
x = x * 3 + 1;
}
answer++;
if (answer == 500) {
return - 1;
}
}
return answer;
}
}📌다른 사람 코드
class Solution {
public int solution(int num) {
int count = 0;
long n = (long)num;
if(n == 1) {
return 0;
}
while(n != 1) {
n = method(n);
count++;
if(count >= 500) {
return -1;
}
}
return count;
}
public static long method(long num) {
return num % 2 == 0 ? num / 2 : (num * 3 + 1);
}
}☘️28.하샤드 수
문제 설명
양의 정수 x가 하샤드 수이려면 x의 자릿수의 합으로 x가 나누어져야 합니다.
예를 들어 18의 자릿수 합은 1+8=9이고, 18은 9로 나누어 떨어지므로 18은 하샤드 수입니다.
자연수 x를 입력받아 x가 하샤드 수인지 아닌지 검사하는 함수, solution을 완성해주세요.
제한 사항
x는 1 이상, 10000 이하인 정수입니다.
예시

☀️내 코드
class Solution {
public boolean solution(int x) {
boolean answer = true;
int num = x;
int sum = 0;
while (num != 0) {
sum += num % 10;
num /= 10;
}
if (x % sum != 0) {
answer = false;
}
return answer;
}
}📌다른 사람 코드
class Solution {
public boolean solution(int x) {
int sum = String.valueOf(x).chars().map(ch -> ch - '0').sum();
return x % sum == 0;
}
}☘️29.3진법 뒤집기
문제 설명
자연수 n이 매개변수로 주어집니다. n을 3진법 상에서 앞뒤로 뒤집은 후, 이를 다시 10진법으로 표현한 수를 return 하도록 solution 함수를 완성해주세요.
제한 사항
n은 1 이상 100,000,000 이하인 자연수입니다.
예시

☀️내 코드
import java.util.ArrayList;
class Solution {
public int solution(int n) {
ArrayList<Integer> list = new ArrayList<>();
int answer = 0;
while (n != 0) {
list.add(n % 3);
n /= 3;
}
int num = 1;
for(int i = list.size() - 1; i >= 0; i--) {
answer += list.get(i) * num;
num *= 3;
}
return answer;
}
}📌다른 사람 코드
class Solution {
public int solution(int n) {
String a = "";
while(n > 0){
a = (n % 3) + a;
n /= 3;
}
a = new StringBuilder(a).reverse().toString();
return Integer.parseInt(a,3);
}
}☘️30.최소직사각형
문제 설명
명함 지갑을 만드는 회사에서 지갑의 크기를 정하려고 합니다. 다양한 모양과 크기의 명함들을 모두 수납할 수 있으면서, 작아서 들고 다니기 편한 지갑을 만들어야 합니다. 이러한 요건을 만족하는 지갑을 만들기 위해 디자인팀은 모든 명함의 가로 길이와 세로 길이를 조사했습니다.
아래 표는 4가지 명함의 가로 길이와 세로 길이를 나타냅니다.
| 명함 번호 | 가로 길이 | 세로 길이 |
|---|---|---|
| 1 | 60 | 50 |
| 2 | 30 | 70 |
| 3 | 60 | 30 |
| 4 | 80 | 40 |
가장 긴 가로 길이와 세로 길이가 각각 80, 70이기 때문에 80(가로) x 70(세로) 크기의 지갑을 만들면 모든 명함들을 수납할 수 있습니다. 하지만 2번 명함을 가로로 눕혀 수납한다면 80(가로) x 50(세로) 크기의 지갑으로 모든 명함들을 수납할 수 있습니다. 이때의 지갑 크기는 4000(=80 x 50)입니다.
모든 명함의 가로 길이와 세로 길이를 나타내는 2차원 배열 sizes가 매개변수로 주어집니다. 모든 명함을 수납할 수 있는 가장 작은 지갑을 만들 때, 지갑의 크기를 return 하도록 solution 함수를 완성해주세요.
제한 사항
- sizes의 길이는 1 이상 10,000 이하입니다.
- sizes의 원소는 [w, h] 형식입니다.
- w는 명함의 가로 길이를 나타냅니다.
- h는 명함의 세로 길이를 나타냅니다.
- w와 h는 1 이상 1,000 이하인 자연수입니다.
예시

☀️내 코드
public class Solution {
public int solution(int[][] sizes) {
int length = 0;
int height = 0;
for (int i = 0; i < sizes.length; i++) {
length = Math.max(length, Math.max(sizes[i][0], sizes[i][1]));
height = Math.max(height, Math.min(sizes[i][0], sizes[i][1]));
}
return length * height;
}
}📌다른 사람 코드
class Solution {
public int solution(int[][] sizes) {
int max = 0;
int min = 0;
for (int[] size : sizes) {
int paramMax = Math.max(size[0], size[1]);
int paramMin = Math.min(size[0], size[1]);
if (paramMax > max) {
max = paramMax;
}
if (paramMin > min) {
min = paramMin;
}
}
return max * min;
}
}