BFS
나를 아는 사람들은 알겠지만 나는 그래프 이론 관련 문제를 안 푼지가 매우 오랜 시간이 지났다. 예전에 백준 팔각형 찍기 (를 빙자한 뱃지 헌팅) 할 때는 꾸역 꾸역 찾아보면서 풀어서 어떻게든 풀어냈지만 사실 근본적인 실력은 매우 낮은 상태였다. 아무래도 DP를 풀면 30분이면 푸는 티어의 문제를 그래프이론 관련된건 3시간은 공부해야 풀리니 당연한 수순이지 않았나 싶다. 이게 사람의 습성인지 본인이 잘하는 것들만 계속해서 풀게된다는 것을 새삼스럽게 느끼게 되었다. 그런데 곧 다가오는 알고리즘 기말고사가 대부분 그래프 이론 관련된 내용이기도 하고, 내가 좋아하는 것만 하면서 뭘 할 수는 없다는 생각이 더 강하게 들고 있어서(당연히 그 전에도 들었지만 회피했을 뿐) 간단한 BFS 문제부터 건들게 되었다. 아마 앞으로 한 3일간은 BFS 문제를 대충 10문제는 두두려 패면서 해결해 봐야지 하는 생각이 든다.
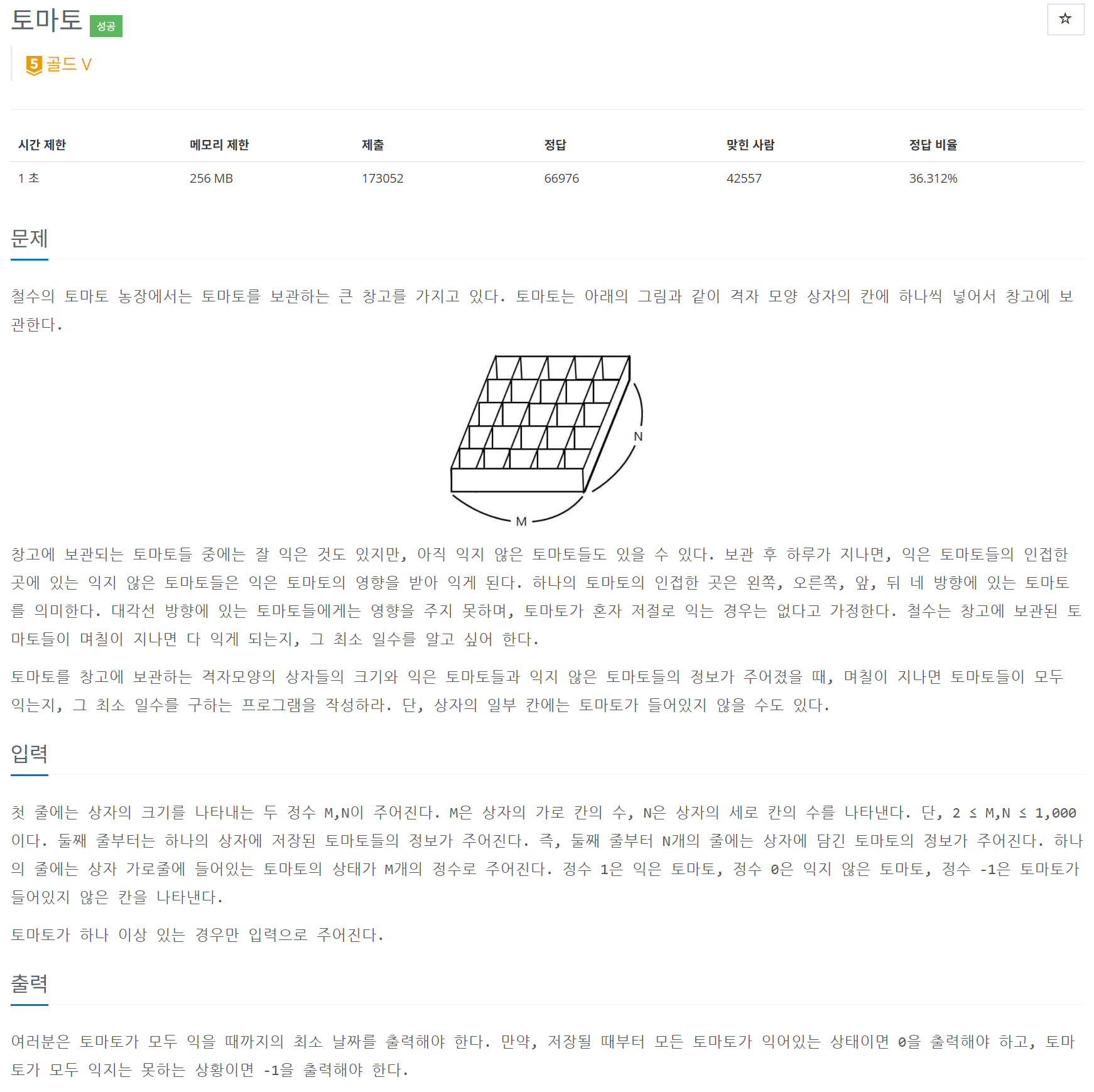
토마토
우선 아무것도 모르는 상태로 문제를 풀기 시작했다. 우선 나는 구현을 통해서 해결해보려는 큰 꿈을 먼저 갖고 있었다. 그냥 1이면 상하좌우 바꿔버리는 코드를 짜서 더 이상 어레이의 총 값에 변화가 없다면 출력을 하고 0이 존재한다면 -1을 출력하는 코드를 작성했다. 생각보다 어렵지 않게 작성하였다. 테스트 케이스에서 계속 이상한 값이 나온다는 것을 깨달았는데 첫 테케처럼 오른쪽 아래에서 실행하면 잘 실행되지만 왼쪽 위에서 실행된다면 타고 가면서 바뀐 값들이 바로바로 변화한다는 것을 깨닫게 되었다. 그래서 이를 해결하기 위해서 배열을 두 개를 사용해야 했고, 기억상 그럴거면 BFS를 찾아보고 푸는게 좋겠다는 생각을 하게 되었다.
내가 느낀 내 코드와 BFS를 사용하는 코드의 핵심은 현 상태의 것을 큐에 저장한다는 것이다. 물론 내가 생각하는 대로 어레이 두 개로 짰어도 아마 실행자체는 되었을 것이다.(아무래도 코드는 매우매우 지저분했겠지만...) 하지만 큐를 생각하자 이전에 풀었던 방식들이 떠올랐고, 바로 코드를 짤 수 있었다. 그렇다고 한 번에 맞췄던 것은 아니다. 빡구현 할 때는 구현해둔 그 0 케이스를 큐를 쓰다보니 놓쳐버려서 다시 추가하는 과정을 통해서 맞출 수 있게 되었다. 오늘까지의 교훈은 아마 큐 개꿀이다! 정도인 것 같지만 이번 학기 끝날때쯤에는 그래프이론 문제를 다양하게 풀 수 있는 상태가 되었으면 좋겠다.
import sys
from collections import deque
M, N = map(int, sys.stdin.readline().split())
arr = [list(map(int, sys.stdin.readline().split())) for _ in range(N)]
queue = deque([])
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]
for i in range(N):
for j in range(M):
if arr[i][j] == 1:
queue.append([i, j])
ans = 0
while queue:
x, y = queue.popleft()
for i in range(4):
xx, yy = dx[i] + x, dy[i] + y
if 0 <= xx < N and 0 <= yy < M:
if arr[xx][yy] == 0:
arr[xx][yy] = arr[x][y] + 1
queue.append([xx, yy])
ans = max(ans, arr[xx][yy])
for i in range(N):
for j in range(M):
if arr[i][j] == 0:
print(-1)
exit()
if ans != 0:
print(ans - 1)
else:
print(ans)아 열심히 좀 살아야하는데 어떻게 매일매일 더 게을러지는지 모르겠다.... 롤부터 지워봐야겠다.