BOJ.5525

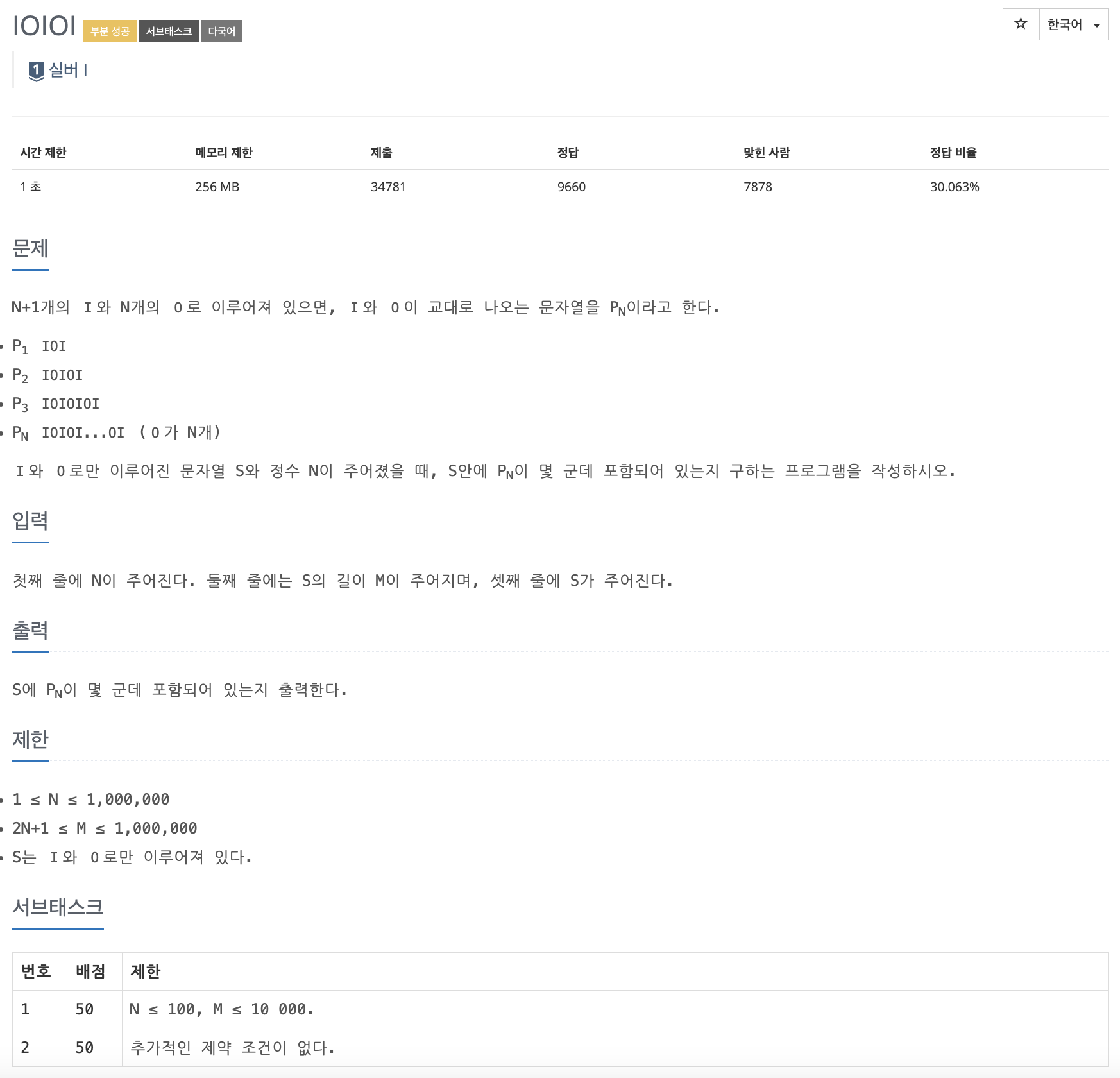
IOIOI

서브태스크 2번을 보자마자 뭔가 알고리즘을 써야지만 단순 구현으로는 해결할 수 없겠다라는 생각이 들었었다. 하지만 티어가 실버1이니깐 그래봤자 별로 어렵지 않겠지 라는 생각으로 구현 중에서 제일 시간 복잡도가 깔끔할 것 같다고 생각이 드는 상태로 문제를 해결하였다. 물론, 당연하게도 서브태스크 2번이 틀리게 나왔다. 코드는 아래와 같다.

import sys

N = int(sys.stdin.readline())
M = int(sys.stdin.readline())
S = sys.stdin.readline().strip()
P = ''
for i in range(2 * N + 1):
   if i % 2 == 0:
       P += 'I'
   else:
       P += 'O'
cnt = 0
for i in range(M):
   if i + 2 * N + 1 > M:
       break
   if P == S[i:i + 2 * N + 1]:
       cnt += 1

print(cnt)

평소에도 문자열 문제를 즐겨 푸는 편은 아니고 특이한 알고리즘 공부할 겸 해서 자주 풀었었는데 클래스 3 정복을 위해서 풀고 있던 문항이라 문자열 시간 단축 방법을 위해서 좀 찾아보니 KMP 알고리즘을 찾을 수 있었다.

KMP 알고리즘

KMP 알고리즘의 기본 원리

KMP 알고리즘의 핵심은 불필요한 비교를 피하기 위해 이미 수행한 비교의 정보를 활용하는 것입니다. 이를 위해 '부분 일치 테이블(Partial Match Table)'을 사용합니다. 이 테이블은 패턴 문자열에서 각 문자 위치에서의 접두사와 접미사의 최대 일치 길이를 저장합니다.

부분 일치 테이블 생성

부분 일치 테이블을 생성하기 위해, 패턴 문자열 자체 내에서 접두사와 접미사가 얼마나 잘 맞는지를 분석합니다. 예를 들어, 패턴이 "ABABAC"라고 가정해 봅시다.

1. 첫 번째 문자 'A'에 대해서는 접두사와 접미사가 없으므로 일치 길이는 0입니다.
2. 두 번째 문자 'B'까지 고려할 때, 접두사 'A'와 접미사 'B'는 일치하지 않으므로 길이는 여전히 0입니다.
3. 세 번째 문자 'A'까지 볼 때, 'ABA'에서 접두사 'A'와 접미사 'A'가 일치하므로 길이는 1입니다.
4. 이런 식으로 계속 분석하여 전체 패턴에 대한 부분 일치 테이블을 완성합니다.

문자열 탐색

본문 문자열을 순회하면서 패턴과 일치하는 부분을 찾습니다. 일치하는 문자가 발견되면 계속해서 다음 문자를 비교합니다. 만약 어느 지점에서 불일치가 발생하면, 부분 일치 테이블을 참조하여 패턴을 적절히 이동시킵니다.

예를 들어, 본문 문자열이 "ABCABABACABCD"이고 패턴이 "ABABAC"일 때, KMP 알고리즘은 다음과 같이 작동합니다:

1. 처음에는 본문의 첫 번째 문자 'A'와 패턴의 첫 번째 문자 'A'가 일치합니다.
2. 계속해서 비교를 진행하다가, 본문의 네 번째 문자 'C'와 패턴의 네 번째 문자 'B'가 일치하지 않습니다.
3. 이때 부분 일치 테이블을 참조하여 패턴을 적절히 이동시키고, 다시 비교를 시작합니다.

이 과정을 통해 KMP 알고리즘은 불필요한 비교를 크게 줄이면서 효율적으로 문자열 검색을 수행할 수 있습니다.

예시 코드

def KMP_search(s, pattern):
    # 부분 일치 테이블 생성
    lps = [0] * len(pattern)
    length = 0
    i = 1
    while i < len(pattern):
        if pattern[i] == pattern[length]:
            length += 1
            lps[i] = length
            i += 1
        else:
            if length != 0:
                length = lps[length-1]
            else:
                lps[i] = 0
                i += 1

    # 문자열 검색
    i = 0 # s의 인덱스
    j = 0 # pattern의 인덱스
    while i < len(s):
        if pattern[j] == s[i]:
            i += 1
            j += 1
        if j == len(pattern):
            print(f"패턴이 {i-j}에서 발견됨")
            j = lps[j-1]
        elif i < len(s) and pattern[j] != s[i]:
            if j != 0:
                j = lps[j-1]
            else:
                i += 1

문제풀이

위의 알고리즘을 기반으로 코드를 수정해서 해결하였다. 다만, 아직도 이게 왜 실1 난이도인지 잘 모르겠다... 아니 근데 KMP 사용하면 최소 골드 상위권 아닌가 후... 암튼 아래에 풀이 업로드하였습니다. 위의 코드를 이용해서 짰습니다.

import sys

def KMP_search(s, pattern):
    # 부분 일치 테이블 생성
    lps = [0] * len(pattern)
    length = 0
    i = 1
    while i < len(pattern):
        if pattern[i] == pattern[length]:
            length += 1
            lps[i] = length
            i += 1
        else:
            if length != 0:
                length = lps[length-1]
            else:
                lps[i] = 0
                i += 1

    # 문자열 검색
    i = 0 # s의 인덱스
    j = 0 # pattern의 인덱스
    count = 0
    while i < len(s):
        if pattern[j] == s[i]:
            i += 1
            j += 1
        if j == len(pattern):
            count += 1
            j = lps[j-1]
        elif i < len(s) and pattern[j] != s[i]:
            if j != 0:
                j = lps[j-1]
            else:
                i += 1
    return count

# 입력 처리
N = int(sys.stdin.readline())
M = int(sys.stdin.readline())
S = sys.stdin.readline().strip()

# 패턴 생성
P = 'I' + 'OI' * N

# KMP 알고리즘을 이용한 검색
cnt = KMP_search(S, P)

# 결과 출력
print(cnt)