Four Squares
최근에 분할정복 문제에 대해서 공부하고 있어서 조만간 뭉텅이로 분할정복 문제가 한 4개 정도 업로드 될 예정이다. 이번주에 전학영 과제가 끝내고 나면 조금 더 여유가 있어질 예정이라서 시간을 내서 그래프 이론에 대해서 공부해보려고 한다. 저번 학기에는 프로젝트 위주의 스터디에서 멘토를 진행했었는데 이번 학기에는 알고리즘 스터디에서 멘토를 진행해보려고 한다. 프로젝트 스터디를 진행하면서 생각보다 현타도 많이 오고 미안한 것도 많아서 개발 공부도 좀 더 하려고 하는데 알고리즘이 요즘 너무 재밌어서 멈출수가 없다. 요즘에 대한 회고는 이쯤에서 마무리 짓고 이 문제에 대해서 적어보려고 한다.
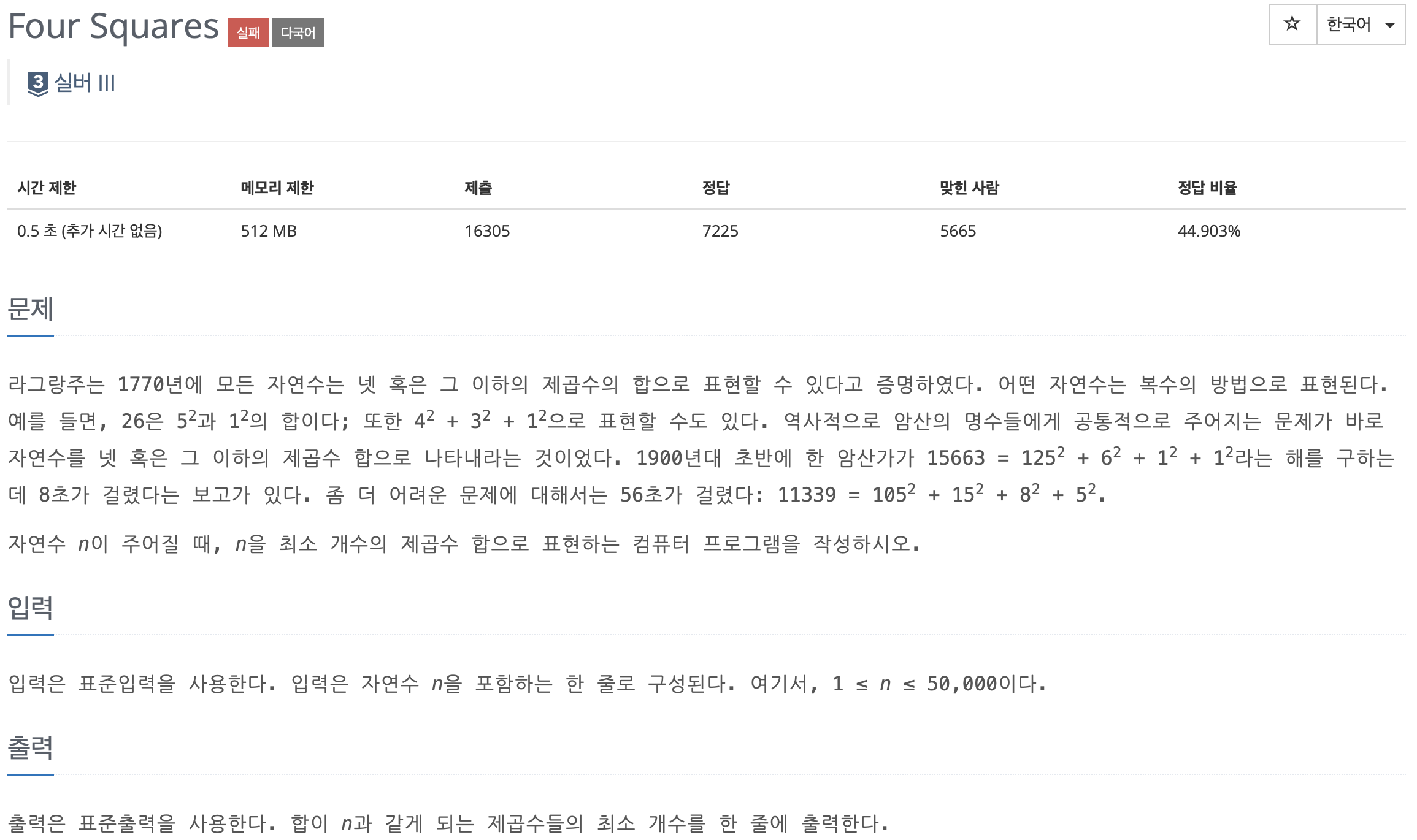
이 문제는 보시다시피 내가 한 번 싶해 했었던 문제이다. 시간 제한이 0.5초인걸로 보아 시간초과가 나오거나 코드가 엄청 길어지고 틀렸습니다가 나왔던 문제일거라고 생각했다. 보시다시피 7개월 전 지금도 코딩 응앤데 더 코딩 응애이던 시절에 문제를 풀었던 흔적이 있다. 브루트 포스로 문제를 해결했던거 같은데 브루트 포스만으로 해결한다면 시간초과가 나올 수 밖에 없는 구조를 갖고 있다. 아무리 n의 범위가 50000개 밖에 되지 않더라도 제곱을 계속해서 돈다면 0.5초는 넘을 수 밖에 없다. 그래서 DP를 추가해서 문제를 풀어보려고 한다.

가장 먼저 추가한 것은 1~225까지의 어레이였다. 시간이 부족하니 동일한 것을 찾을 때에도 이분 탐색을 사용하면 좋을 것 같단 생각이 들긴 하였는데 225개라면 사실 그냥 어떻게 찾아도 금방 찾는다. 그래서 이후에는 dp의 구조를 고민하였다. 숫자가 아래서부터 올라간다면 각 수를 구하는 과정에 대한 최적화가 정해질 것이고, 범위 자체가 정해져 있기 때문에 그냥 수만 올라간다면 해결될 것이라고 생각하였다. 예를 들어서 설명하자면 4는 2*2가 최적이라는 것을 알 수 있다. 그러면 7을 구할 때는 4가 먼저 빠지고 3에 대해서 오 3의 최적값은 이미 구해놓은걸 가져다가 쓸 수 있다. 그 외의 경우의수는 7을 1과 6으로 나누는 경우의수 밖에 없기 때문에 4와 3으로 나누는 경우의 수가 더 적다는 것을 알 수 있고 이는 이후에 찾을 수에 또 사용할 데이터가 되는 것이다. 설명을 좀 개떡같이 해놨는데 코드를 보면 이해가 될 것이라고 생각한다. 주석 다는건 너무너무 귀찮으니 넘어가도록 하자. (P.S. 이 문항은 실버4 문항인데 1699번의 실버 2 문항까지 한 번에 날먹할 수 있는 문항이니 꼭 풀어보도록 하자! 스터디 횐님들~^^)
#include <iostream>
#include <algorithm>
using namespace std;
int main(){
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int n;
cin >> n;
int dp[110000];
dp[1] = 1;
for(int i = 1; i<= n; i++){
dp[i] = dp[1] + dp[i -1];
for(int j = 2; j * j <= i; j++){
dp[i] = min(dp[i], 1+ dp[i - j * j]);
}
}
cout << dp[n];
}