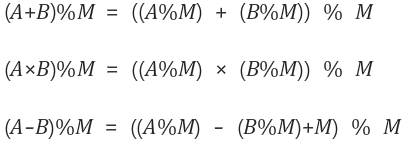https://www.acmicpc.net/problem/10430
백준 10430문제를 풀기 위해선 모듈러연산에 대한 이해가 필요하다.
모듈러 연산은 mod m일때, 항상 0 ~ m의 범위를 가지는 값을 결과 값으로 가지게 된다.
만약 음수의 결과 값을 가진다면 절대 값을 취한 값에서 mod를 한 결과를 m을 더하거나 m을 2배, 3배한 값을 더해 0 ~ m의 범위의 결과 값을 가지도록 하면 된다.
모듈러 연산의 예시
17 mod 5 = 2
20 mod 3 = 2
음수일 때
-3 mod 11 = 8
-11 mod 11 = 0
-1 mod 11 =10
> 2. 모듈러 합동
(a mod n) = (b mod n) -> a ≡ b(mod n)
어떤 값 A와 B가 n으로 나누었을 때 나머지가 같다면 A와 B는 모듈 C에 대한 합동 관계라고 한다.
그러한 A와 B는 A - B를 하였을 때 k*n과 같다.
즉, A - B = kn으로 나타낼 수 있다.
예를들어보자.
4와 9는 mod 5로 인해 나머지가 4로 동일하다.
4 - 9 = -5 = -1*5로 나타낼 수 있다.
이로인해 다음과 같이 합동의 특성을 볼 수 있다.
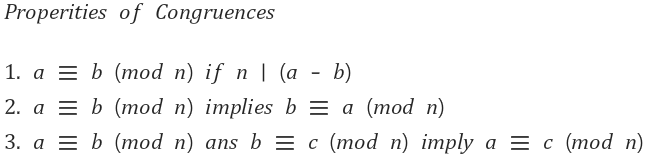
- 모듈러 연산의 속성
- (a + b) mod n = ((a mod n) + (b mod n)) mod n
- (a - b) mod n = ((a mod n) - (b mod n)) mod n
- (a x b) mod n = ((a mod n) * (b mod n)) mod n
<참고>
((a mod n) - (b mod n)) mod n에서 a = 3, b = 5, n = 6이면
-2 mod 6 = -2가 나온다.
이때 '-' 연산을 이용할 때 mod를 쓰는 일이 있다면
((a mod n) - (b mod n)) mod n + n을통해 양수로 만들어 줄 수 있다.
[증명 1] : (A+B) %C = (A%C + B%C)%C
증명 과정 자체는 매우 간단하다.
위 공식대로 풀면 되는데 하나하나 설명해보겠다.
먼저 a 와 b에 대해 c로 나눈 나머지 값을 mod 로 표현하여 정의한다. (이때 T 와 S 는 a 와 b 의 나머지다)

그럼 a와 b에 대하여 식을 변형 할 수 있는데 그게 바로 아래와 같은 것이다.

증명하려는 식에 대입해보고 식을 정리해보자.
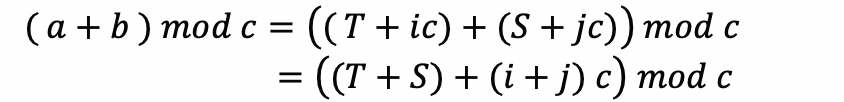
위 식에서 느낌이 오는가?
c = 0 이 아닌 이상 ( i + j )*c 는 0 또는 3의 배수다.
이 말은 i 와 j 의 값에 상관 없이 c의 배수이기 때문에 ( i + j )*c mod c = 0 이다.
즉 나머지 연산에서 ( T + S ) 의 나머지에 대하여 ( i + j )*c 는 위 식의 나머지 값에 대햐여 아무런 영향을 미치지 못한다.
그러므로 다음과 같이 쓸 수 있다.
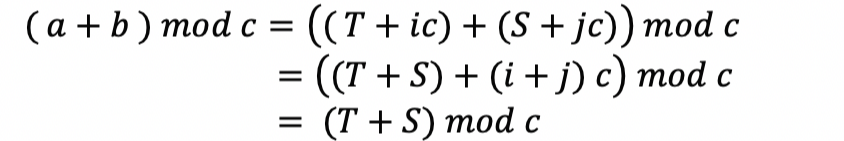
그리고 T 와 S 는 처음 정의했듯이 각 각 a mod c 와 b mod c 이므로 이들로 교체해주면 우리가 증명하고자 한 공식이 완성된다.
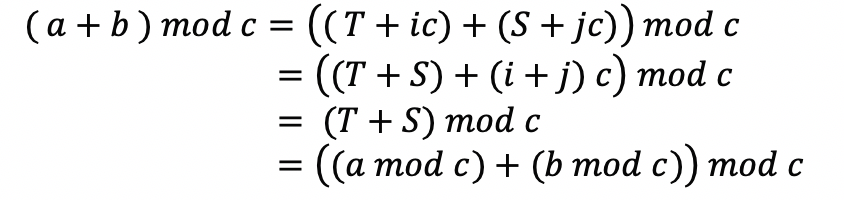
증명 완료
[증명2] : (AxB)%C = (A%C x B%C)%C
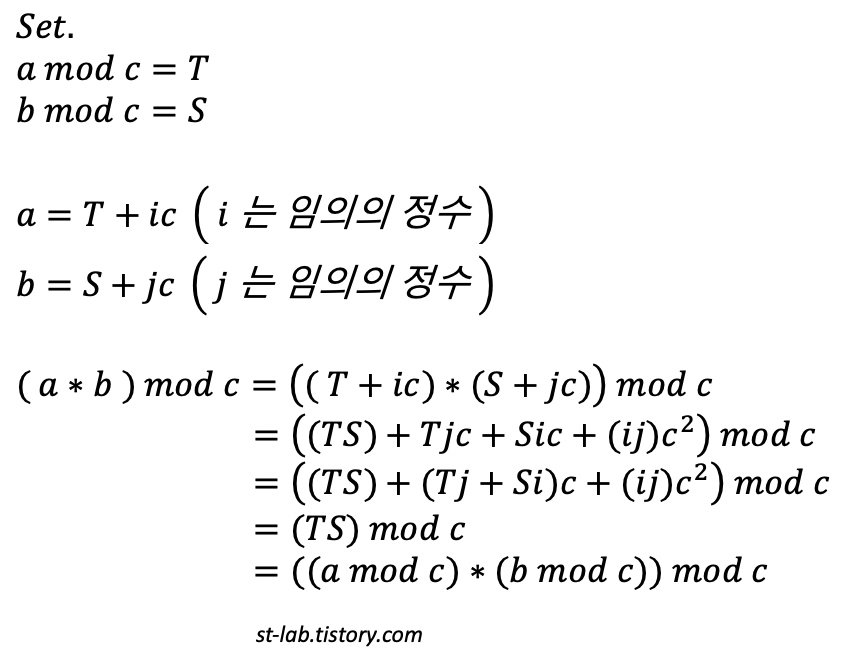
마찬가지로 곱셈을 풀어준 뒤 c 로 묶인 것들은 나머지 값에 영향을 미치지 못하므로 생략해주면 위 같이 공식이 성립함을 볼 수 있다.
백준문제풀이(10430)
include <stdio.h>
int main()
{
int A, B, C;
scanf("%d %d %d", &A, &B, &C);
printf("%d\n", (A + B) % C);
printf("%d\n", (A % C + B % C) % C);
printf("%d\n", (A * B) % C);
printf("%d\n", (A % C * B % C) % C);
return 0;
}