시소 짝꿍
https://school.programmers.co.kr/learn/courses/30/lessons/152996
문제

이 문제를 이해하는데 오랜 시간이 걸렸다.
예를 들어서 [180, 180, 180, 180, 180, 270, 270, 270, 270]이라 할 때
180, 270은 3m, 2m에서 균형을 이룬다는 것은 알고 있다.
처음엔 유니크값으로 {180, 270}이렇게 하나만 될 줄 알았으나 그렇지 않았다.
서로 다른 사람 몸무게이고 같은 무게지만 다른 값이다. 즉 유니크하지 않다.
그래서 첫 번째 180과 조합을 이루는 값은 270 => (4개)가 될 것이고 마찬가지로 두 번째 180도 270 => (4개)가 될 것이다.
즉 180(5개) * 270(4개) => 20개가 된다.
또한 같은 무게 일때도 생각을 해야한다.
[180, 180, 180, 180, 180]이고 이 중 2개를 뽑는 것은 5C3과 같다.
즉 (5*4)/2 => 10이다.
마찬가지로 [170, 170, 170, 170]일 때도 생각을 해야한다.
(4*3)/2 => 6이다.
즉 답은 다 더한값인 20+10+6=36이 된다.
풀이
문제에서 weights의 길이는 100,000이다. 상당히 큰 값이다. 처음엔 이중for문으로 풀었지만 역시나 TLE가 발생하였다.
해결책으로 딕셔너리를 사용하였다.
-
weights의 원소들 딕셔너리에 개수형태로 저장한다.
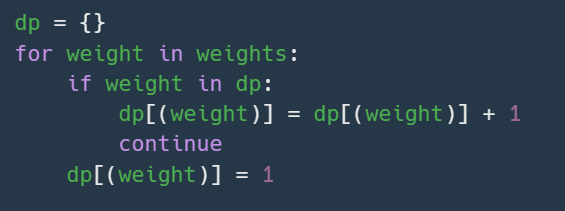
개수형태로 저장하는 이유는 앞서서 설명했다시피 개수를 알면 쉽게 풀 수 있기 때이다. -
가능한 조합을 배열로 나타낸다.

문제에서 시소는 2, 3, 4만큼 길이가 주어줬고 길이가 같을 때에는 1로 정의할 수 있다.
예를 들어서 2x = 3y라고 할 때 (2/3)x =y라고 할 수 있다. -
만약 (180, 270)을 구했으면 (270, 180)은 안해도 된다. 즉 계산 결과를 저장할 딕셔너리를 선언한다.

-
앞서 만든 배열 arr와 weight을 곱한 값이 dp안에 있으면 해당 weight은 균형을 만들 수 있다는 것이다. 이것을 코드로 나타내면 다음과 같다.
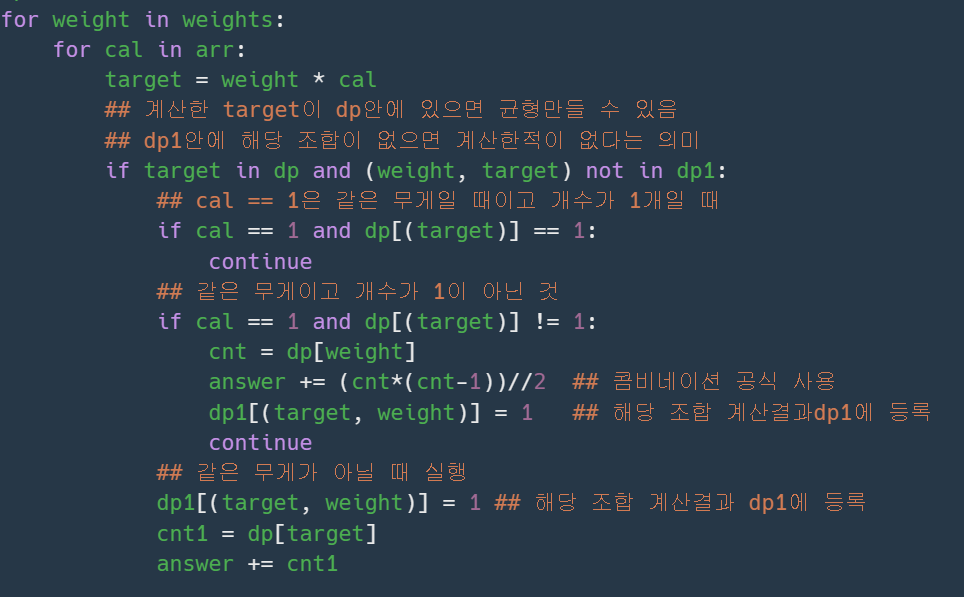
위에서 설명했다시피 같은 무게일 때(cal == 1)일 때에는 콤비네이션 공식 (개수가 1이상일 때만 허용)
같은 무게가 아닐 때에는 target에 개수를 더한다.
def solution(weights):
dp = {}
for weight in weights:
if weight in dp:
dp[(weight)] = dp[(weight)] + 1
continue
dp[(weight)] = 1
answer = 0
arr = [1, 2 / 3, 2/4, 3/2, 3/4, 4/2, 4/3]
dp1 = {}
for weight in weights:
for cal in arr:
target = weight * cal
## 계산한 target이 dp안에 있으면 균형만들 수 있음
## dp1안에 해당 조합이 없으면 계산한적이 없다는 의미
if target in dp and (weight, target) not in dp1:
## cal == 1은 같은 무게일 때이고 개수가 1개일 때
if cal == 1 and dp[(target)] == 1:
continue
## 같은 무게이고 개수가 1이 아닌 것
if cal == 1 and dp[(target)] != 1:
cnt = dp[weight]
answer += (cnt*(cnt-1))//2 ## 콤비네이션 공식 사용
dp1[(target, weight)] = 1 ## 해당 조합 계산결과dp1에 등록
continue
## 같은 무게가 아닐 때 실행
dp1[(target, weight)] = 1 ## 해당 조합 계산결과 dp1에 등록
cnt1 = dp[target]
answer += cnt1
return answer 결과